A partir de datos del INE el año 2006 tenemos los siguientes datos, por comunidades autónomas, sobre recursos hídricos (con la codificación de las variables que a continuación se especifica):

He recogido estadísticas de los jugadores de baloncesto del F.C.Barcelona y del R.Madrid publicadas en la página web de la ACB. La base de datos es la siguiente:

PUN=Puntos medios por partido.

T2, T3 y T1=Porcentaje de acierto en tiros de 2, de 3 y de 1, respectivamente.

RTO=Rebotes totales.

ASI=Asistencias.

BRE=Balones recuperados.

BPE=Balones perdidos.

TFA=Tapones a favor.

TCO=Tapones en contra.

FFA=Faltas a favor.

FCO=Faltas en contra.

Si se hace un Análisis de componentes principales con estas variables obtenemos el siguiente cuadro del peso de cada una de las componentes:

Las tres primeras componentes explican el 73,1% de la variabilidad. Con las dos primeras un 62,4%.

Los coeficientes de las tres primeras componentes son las siguientes:

El gráfico de las dos primeras componentes principales es el siguiente:

A partir de nuestra base de datos adjunta del artículo Explotación de una base de datos 1: Base de datos podemos realizar Análisis factorial. Veamos algunos ejemplos:

1. Hacer un Análisis factorial con las variables P1, P2, P3, P4, P5, P6 y P7. Ver cuánta variabilidad explican los factores.

2. Hacer un giro de los ejes que consiga la máxima capacidad explicativa de los factores.

3. Representar los cien pacientes en ejes formados por los factores encontrados.

4. Proyectar en la representación de los ejes de los factores la variable P8.

5. Proyectar en la representación de los ejes de los factores la variable Cirugía.

6. Proyectar en la representación de los ejes de los factores la variable Sexo.

7. Proyectar en la representación de los ejes de los factores la variable Departamento.

SOLUCIONES

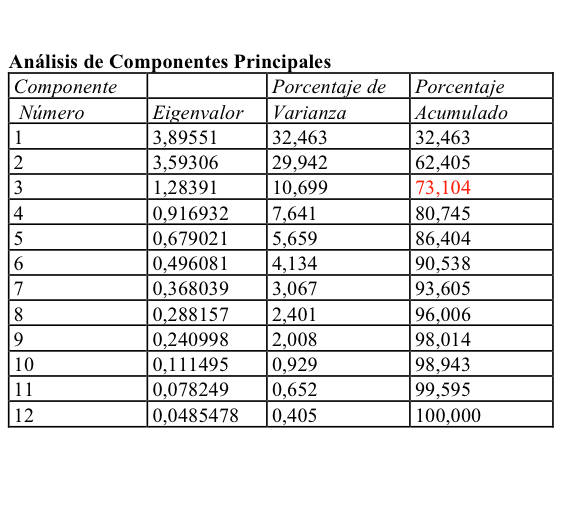
1. Hacer un Análisis factorial con las variables P1, P2, P3, P4, P5, P6 y P7. Ver cuánta variabilidad explican los factores:

Obsérvese que con tres factores explicamos un 93,5% de la información. Esto es mucho, realmente.

2. Hacer un giro de los ejes que consiga la máxima capacidad explicativa de los factores:

Con la rotación variamax conseguimos realmente tres factores claramente delimitados. Observemos que en el primer factor las variables con peso son la P3, P4 y P5. En el segundo son P6 y P7. En el tercer factor son P1 y P2 las que tienen el protagonismo. Esto cuadra con lo que hemos visto al analizar las correlaciones en el fichero 3 de esta serie.

3. Representar los cien pacientes en ejes formados por los factores encontrados:

4. Proyectar en la representación de los ejes de los factores la variable P8:

Observemos que los pacientes que consideran su problema resuelto tienen mucho de todos los factores, pero hay un grupo que tienen valor bajo del primer factor, pero nunca de los otros dos. Los que consideran que su problema no ha quedado resuelto estos están mayoritariamente próximo al vértice donde los tres factores tienen valores bajos.

5. Proyectar en la representación de los ejes de los factores la variable Cirugía:

A los que se ha aplicado Cirugía siguen un patrón similar al seguido con la P8.

6. Proyectar en la representación de los ejes de los factores la variable Sexo:

Aquí no parece haber un patrón determinado. Todo está muy disperso.

7. Proyectar en la representación de los ejes de los factores la variable Departamento:

Si se observa con detalle el gráfico puede apreciarse que el departamento 3, que es Urología, es el departamento que tiene valoraciones más bajas. Sus valores están preferentemente en el extremo de los valores bajos de los tres factores.

A nuestra base de datos adjunta en el artículo Explotación de una base de datos 1: Base de datos le podemos aplicar también el ANOVA. Veamos algunos ejemplos:

1. Comparar la variable Valoración general según el Departamento.

2. Comparar la variable P6 según el Departamento.

SOLUCIONES

1. Comparar la variable Valoración general según el Departamento:

Como hay cuatro departamentos en nuestro estudio deberemos aplicar un ANOVA. Para ello vamos a comprobar, en primer lugar, la normalidad de cada uno de los cuatro grupos a comparar.

Si observamos el Shapiro-Wilk observamos que ninguno de los cuatro grupos se ajusta a la distribución normal. Por lo tanto, vamos a aplicar el Test de Kruskal-Wallis:

Las comparaciones múltiples (en este caso mediante el método Bonferroni-Dunn):

Por lo tanto, el causante de las diferencias entre los cuatro departamentos es el 3, el departamento de Urología.

2. Comparar la variable P6 según el Departamento:

Como la variable respuesta ahora, la variable P6, es una variable tipo Likert, podemos ya directamente aplicar un Test de Kruskal-Wallis. Conceptualmente este tipo de variables no se ajusta bien nunca a una distribución normal. Son muy pocos los valores que contempla. Es verdad que tampoco es continua, pero es más oportuno, en este caso, aplicar este Test por la mucha mayor versatilidad que tiene.

Como rechazamos la Hipótesis nula de igualdad de grupos, debemos aplicar unas comparaciones múltiples:

Como puede verse, la única diferencia apreciable es la que hay entre los departamentos 3 y 4. Las otras comparaciones no muestran diferencias significativas.

A nuestra base de datos adjunta en el artículo Explotación de una base de datos 1: Base de datos le podemos aplicar diferentes comparaciones de dos poblaciones. Veamos algunos ejemplos:

1. Compobar si hay diferencias significativas en cuanto a la Valoración general entre los hombres y mujeres. Calcular la d de Cohen si es que antes se comprueba que la diferencia es estadísticamente significativa.

2. Comparar la Valoración general entre los operados y no operados. Calcular la d de Cohen si es que antes se comprueba que la diferencia es estadísticamente significativa.

3. Comparar si los dos grupos formados por la variable P8 tienen valores diferentes, significativamente, en cuanto a la variable Valoración. Calcular la d de Cohen si es que antes se comprueba que la diferencia es estadísticamente significativa.

SOLUCIONES:

1. Compobar si hay diferencias significativas en cuanto a la Valoración general entre los hombres y mujeres. Calcular la d de Cohen si es que antes se comprueba que la diferencia es estadísticamente significativa:

Se trata de variables continuas, muestras independientes, por lo tanto, hace falta comprobar la normalidad de cada una de las dos muestras:

Debemos, pues, aplicar el Test de Mann-Whitney:

No hay diferencias significativas entre los dos sexos, por lo tanto no tiene sentido aplicar aquí la d de Cohen.

2. Comparar la Valoración general entre los operados y no operados. Calcular la d de Cohen si es que antes se comprueba que la diferencia es estadísticamente significativa:

Se trata de variables continuas, muestras independientes y, por lo tanto, hemos de comprobar la normalidad de cada una de las dos muestras:

Como no hay normalidad debemos aplicar el Test de Mann-Whitney:

No hay diferencias significativas entre los dos grupos, por lo tanto, no debemos aplicar la d de Cohen.

3. Comparar si los dos grupos formados por la variable P8 tienen valores diferentes, significativamente, en cuanto a la variable Valoración. Calcular la d de Cohen si es que antes se comprueba que la diferencia es estadísticamente significativa:

Se trata de variables continuas, muestras independientes y hace falta, pues, ahora comprobar la normalidad de cada una de las dos muestras:

Como no hay normalidad aplicamos el Test de Mann-Whitney:

Ahora sí que vemos diferencias significativas entre los dos grupos. Ahora sí tiene sentido aplicar la d de Cohen.

A partir de nuestra base de datos adjunta del artículo Explotación de una base de datos 1: Base de datos podemos realizar regresiones múltiples. Veamos algunos ejemplos:

1. Realizar una Regresión lineal múltiple entre la variable Valoración general y P1, P2, P3, P4, P5, P6 y P7. Se pretende pronosticar la Valoración general que daría un paciente a partir de los valores de los 7 primeros ítems de la encuesta.

 2. Realizar un Regresión lineal múltiple entre la variable Valoración general y las variables Edad y Días de ingreso.

SOLUCIONES:

1. Realizar una Regresión lineal múltiple entre la variable Valoración general y P1, P2, P3, P4, P5, P6 y P7. Se pretende pronosticar la Valoración general que daría un paciente a partir de los valores de los 7 primeros ítems de la encuesta:

Las correlaciones entre todas estas variables son las siguientes:

Viendo cuáles son las correlaciones entre la variable respuesta o dependiente y las variables explicativas o independientes ya podemos intuir por dónde irá el modelo elegido finalmente. Veamos cuál es:

Ya vemos cuáles son los coeficientes significativos. Vemos también que la r cuadrado es muy buena.

Apliquemos un Stepwise:

2. Realizar un Regresión lineal múltiple entre la variable Valoración general y las variables Edad y Días de ingreso:

Las correlaciones entre la variable respuesta y las dos variables explicativas son las siguientes:

El modelo es:

Y al aplicar un Stepwise:

Y si nos fijamos bien veremos que al final hemos acabado en un modelo de Regresión lineal simple que es el que hemos estimado en cuando estábamos aplicando esa técnica a nuestra base de datos.

A partir de nuestra base de datos adjunta del artículo Explotación de una base de datos 1: Base de datos podemos hacer distintas regresiones lineales simple. Veamos algunos ejemplos:

1. Hacer una Regresión lineal simple entre las variables Edad y Valoración general. Se pretende pronosticar en el futuro la variable Valoración general a partir de la variable Edad.

2. Hacer una Regresión lineal simple entre P6 y P7. Se pretende pronosticar en el futuro el valor de la variable P7 a partir del conocimiento del valor de la variable P6. O sea, se pretende pronosticar cómo siente el paciente el nivel de información recibido a partir de su valoración acerca del personal médico.

SOLUCIONES:

1. Hacer una Regresión lineal simple entre las variables Edad y Valoración general. Se pretende pronosticar en el futuro la variable Valoración general a partir de la variable Edad:

La recta de regresión es la siguiente:

La recta es la negra. Las dos rectas rojas y las dos azules son intervalos de confianza del 95% de la media de una predicción (las rojas) y de un valor individual (las azules).

Los coeficientes del modelo son los siguientes:

Se trata, pues, de una regresión con coeficientes significativos pero con un coeficiente de determinación muy bajo, con una r cuadrado sólo de un 10.25%. Menos de un 50% se considera una muy mala capacidad predictiva de un valor individual de la variable respuesta o dependiente.

2. Hacer una Regresión lineal simple entre P6 y P7. Se pretende pronosticar en el futuro el valor de la variable P7 a partir del conocimiento del valor de la variable P6. O sea, se pretende pronosticar cómo siente el paciente el nivel de información recibido a partir de su valoración acerca del personal médico:

La recta de regresión es, ahora:

Los coeficientes del modelo:

Ahora tenemos una mejor capacidad de determinación, un 70.87%.

A nuestra base de datos adjunta en el artículo Explotación de una base de datos 1: Base de datos le podemos analizar la relación entre variables cualitativas. Veamos algunos ejemplos:

1. Analizar la relación entre la variable Sexo y Cirugía.

2. Analizar la relación entre la variable Cirugía y Departamento.

3. Analizar la relación entre la variable Departamento y P8.

4. Analizar la relación entre la variable Departamento y Cirugía, calculando la V de Cramer si existe relación significativa.

SOLUCIONES

1. Analizar la relación entre la variable Sexo y Cirugía:

2. Analizar la relación entre la variable Cirugía y Departamento:

3. Analizar la relación entre la variable Departamento y P8:

4. Analizar la relación entre la variable Departamento y Cirugía, calculando la V de Cramer si existe relación significativa:

A nuestra base de datos adjunta en el artículo Explotación de una base de datos 1: Base de datos le podemos calcular correlaciones entre variables cuantitativas. Veamos algunos ejemplos:

1. Calcular la correlación de Pearson entre las variables cuantitativas Edad, Días de ingreso y Valoración general.

2. Calcular la correlación de Spearman entre esas mismas variables.

3. Calcular la correlación de Spearman entre las variables P1, P2, P3, P4, P5, P6 y P7.

4. A partir de lo visto en el apartado anterior crear grupos con buena consistencia interna, con alto valor de alfa de Cronbach.

SOLUCIONES

1. Calcular la correlación de Pearson entre las variables cuantitativas Edad, Días de ingreso y Valoración general:

2. Calcular la correlación de Spearman entre esas mismas variables:

3. Calcular la correlación de Spearman entre las variables P1, P2, P3, P4, P5, P6 y P7:

4. A partir de lo visto en el apartado anterior crear grupos con buena consistencia interna, con alto valor de alfa de Cronbach:

Observemos que las combinaciones que tienen alta correlación son los grupos:

P1-P2

P3-P4-P5

P6-P7

Sólo tiene sentido calcular la alfa de Cronbach en estos tres grupos. Para ver cómo se calcula este índice ver el artículo Alfa de Cronbach. La forma más cómoda de cálculo es a partir de la correlación:

Con P1 y P2 el valor es:

2×0,8326/(1+0,8325)=0,9086.

Con P6 y P7:

2×0,8501/(1+0,8501)=0,9189

Con P3, P4 y P5, como el promedio de las tres correlaciones dos a dos entre estas variables es 0,8888:

3×0,8888/(1+2×0,8888)=0,9599

Como podemos ver consistencias internas muy elevadas.

A nuestra base de datos adjunta en el artículo Explotación de una base de datos 1: Base de datos le podemos calcular muchas cosas de Estadística descriptiva. Veamos algunos ejemplos:

1. Hacer una Estadística descriptiva de las variables cuantitativas: Edad, Días de ingreso y Valoración general.

2. Hacer una Estadística descriptiva de las variables cualitativas: Sexo, Cirugía, Departamento y P8.

3. Hacer una Estadística descriptiva de las variables P1 y P6 como ejemplos de dos de las siete variables Likert.

4. Representar de la forma más apropiada y resumida, con Media y Desviación estándar o Mediana y Rango intercuartílico, las variables Edad, Días de ingreso y Valoración general.

SOLUCIONES:

1. Hacer una Estadística descriptiva de las variables cuantitativas: Edad, Días de ingreso y Valoración general:

La variable Edad tiene los siguientes valores de los más importantes estadísticos descriptores:

El Box-Plot:

La variable Días de ingreso tiene los siguientes valores de los más importantes estadísticos descriptores:

Y el Box-Plot:

La variable «Valoración general» tiene los siguientes valores de los más importantes estadísticos descriptores:

Y el Box-Plot:

2. Hacer una Estadística descriptiva de las variables cualitativas: Sexo, Cirugía, Departamento y P8:

Para la variable cualitativa «Sexo» la tabla de frecuencias es:

Y el diagrama de frecuencias:

Para la variable cualitativa «Cirugía» la tabla de frecuencias es:

Y el diagrama de frecuencias:

Para la variable «Departamento»:

Y el diagrama de frecuencias:

Para la variable P8:

Y el diagrama de frecuencias:

3. Hacer una Estadística descriptiva de las variables P1 y P6 como ejemplos de dos de las siete variables Likert:

Para la variable P1:

Para la variable P6:

4. Representar de la forma más apropiada y resumida, con Media y Desviación estándar o Mediana y Rango intercuartílico, las variables Edad, Días de ingreso y Valoración general:

De las tres variables la única que tiene una suficiente aproximación a la normalidad (Asimetría estandarizada y Curtosis estandarizada entre -2 y 2) es la variable «Valoración general», por lo tanto esta sería la única que se podría representar mediante la Media y la Desviación estándar. Las otras dos sería más apropiado hacerlo mediante la Mediana y el Rango intercuartílico. O sea, sería de esta forma:

Edad: 47 (40, 69)

Días de ingreso: 4 (2, 8)

Valoración general:  6,3 ± 1,66