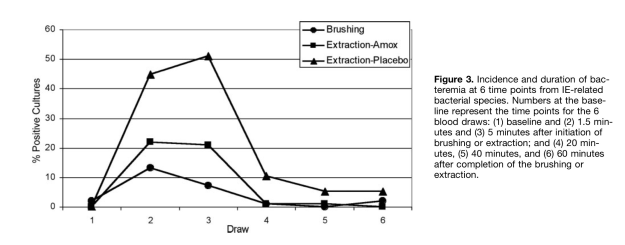
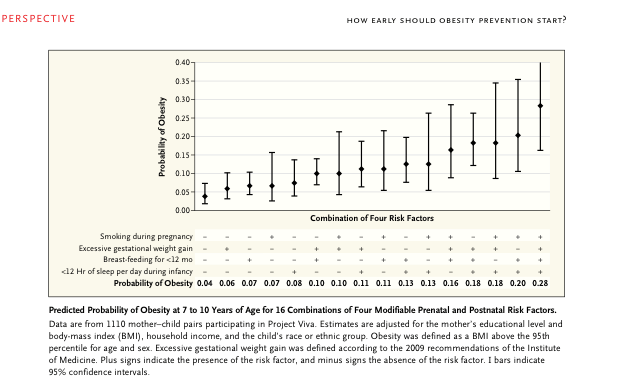
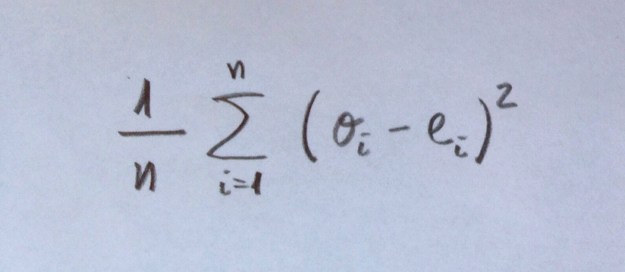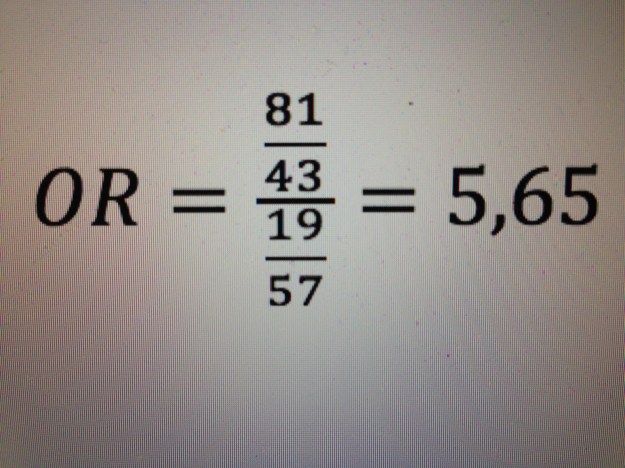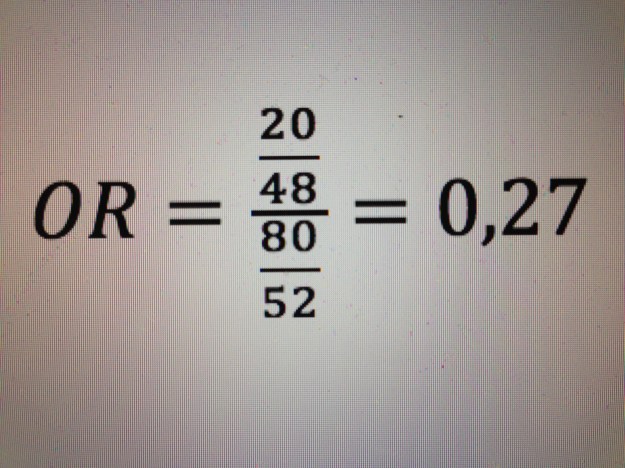La modelización matemática es utilizada con mucha frecuencia en Medicina. Es especialmente usada en Medicina preventiva donde es muy frecuente construir modelos de predicción, modelos para evaluar y cuantificar grados de riesgo.
En todas las revistas médicas vemos con mucha frecuencia modelos matemáticos predictivos. En el día a día, en Medicina, usamos muchos de estos modelos. Por citar sólo unos ejemplos: El Framingham risk score, el EuroSCORE, el APACHE, etc.
Una buena parte de estos modelos, en Medicina, son modelos de Regresión logística. La Regresión logística es, digamos, un modelo matemático extraordinariamente ligado a la Medicina. En Medicina con mucha frecuencia nos preocupa el valor de una variable dicotómica: Muere al año de ser operado el paciente o no. Tiene metástasis a los 5 años o no. Ha tenido un infarto o no. Tiene la presión por encima de 140 ó no. Tiene diabetes o no, etc. Y esta variable dicotómica, digamos variable resultado (en terminología Estadística la solemos denominar «variable dependiente»), queremos ver qué relación, qué asociación tiene con otra u otras variables (variables que en Estadística solemos denominar «variables independientes»).
Relacionar cualquiera de estas variables dicotómicas con alguna o algunas variables es, digamos, consustancial a la labor de la Medicina. Es por esto que el modelo matemático y estadístico más usado en Medicina, de largo, es el de la Regresión logística y los principales usuarios de este tipo de modelos son, evidentemente, también, los médicos.
Ahora bien, un modelo es una maqueta matemática de una realidad. Y como maqueta que es puede ser más o menos próxima a la realidad. Hay buenas modelizaciones y malas modelizaciones. Y, por supuesto, toda una inmensa escala de situaciones intermedias que conviene saber distinguir, evaluar y pesar.
Hay todo un amplio repertorio de conceptos que se manejan habitualmente en la modelización. La intención de este artículo es aclarar un poco este bosque inmenso de conceptos para ver qué significa cada uno de ellos. Nos vamos a centrar, en concreto, a la hora de manejar ejemplos, en la modelización mediante Regresión logística, por ser la más habitual en Medicina, pero todos los conceptos que vamos a ver son extrapolables a la modelización usando cualquier otro modelo y en cualquier campo del conocimiento, evidentemente.
Validación, Validación interna, Validación externa, Ajuste, Discriminación, Calibración, Reproductividad, Transportabilidad son conceptos que aparecen habitualmente en este ámbito generando este bosque conceptual por el que es ciertamente difícil moverse.
Todos estos conceptos conllevan, en definitiva, procedimientos matemáticos y estadísticos distintos con los que evaluar la calidad de una modelización. Vamos a internar ir delimitando, poco a poco, cada uno de estos importantes conceptos.
Como vamos a ver cada uno de estos criterios en un modelo de Regresión logística es importante, en primer lugar, recordar un poco lo que es y representa la modelización mediante este especial tipo de Regresión.
Un modelo de Regresión logística es importante, en primer lugar, que se vea dibujado. Si únicamente tenemos una variable independiente el modelo se dibuja así:
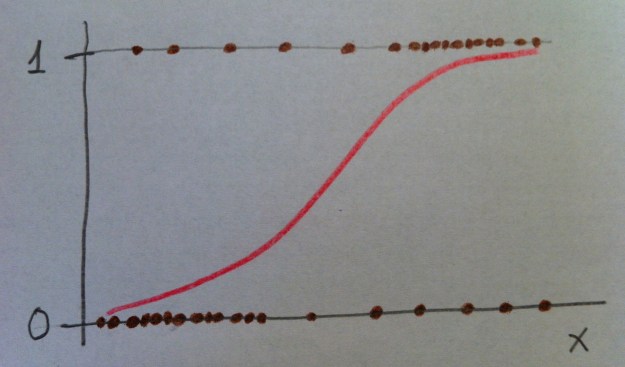
Observemos que se trata de una variable dependiente codificada con 0 y 1 y una variable independiente x. Los puntos representan los valores concretos de una muestra: lo pacientes. Como la variable dependiente es dicotómica (codificada con 0 y 1), los valores únicamente pueden estar a nivel del 0 ó a nivel del 1.
El modelo construye una curva que se adapte lo más fielmente posible a los datos, que en el dibujo anterior es la curva dibujada en color rojo. Para más detalles puede consultarse, en este blog, el Tema 11: Regresión logística.
Vayamos con los conceptos.
Validación: La validación significa evaluar lo válido, lo correcto, lo firme que es un procedimiento. En el ámbito de la modelización, como estamos dibujando una realidad con materiales tomados de otra realidad (en nuestro caso hablamos de evaluar riesgos en la vida real mediante herramientas tomadas del mundo de las funciones matemáticas), la validación evalúa lo estrecha que es esta representación, lo próximo que es ese dibujo matemático a la realidad que trata de representar.
Validación es, pues, un término muy genérico porque esta evaluación se puede hacer mediante criterios diferentes y mediante procedimientos también muy diferentes. Por lo tanto, como vamos a ver a continuación, la noción de validación va abriéndose a distintos conceptos.
Suele diferenciarse entre Validación interna y Validación externa. Veamos esa importante distinción:
Validación interna: Cuando esa evaluación se hace con los propios datos de la realidad que te han servido o que has usado para construir el modelo. Se trata, por lo tanto, de ver el grado de conexión que hay entre lo que nos dice el modelo matemático creado y los propios datos usados para construir ese modelo. Por eso se le denomina «interna», porque es respecto a los propios datos usados.
Validación externa: Cuando esa evaluación se hace no con los propios datos usados para construir el modelo sino con otros datos, con otra muestra. Se trata, pues, de una generalización. Aquí no se trata, pues, de evaluar la proximidad del modelo con los datos usados para construirlo, sino, por el contrario, se trata de ensayar, de poner a prueba el modelo para ver si explican también otros valores, si explican una realidad análoga a la representada pero de la que no hemos usado datos a partir de los cuales construir el modelo.
En realidad, estos dos conceptos es en torno a los cuales gira todo lo que estamos explicando aquí, puesto que ahora se trata de ir perfilando los diferentes conceptos que van concretando aspectos diferentes de ese proceso de validación tanto interna como externa.
Ajuste: La noción muy utilizada de Ajuste significa la evaluación de la proximidad de un modelo a una determinada realidad. Por lo tanto, todas las técnicas que evalúan el ajuste de unos datos a un modelo son, en realidad, técnicas de validación. Hemos visto en este blog muchos casos de técnicas de ajuste. Lo hemos visto en distintos momentos y tenemos diferentes ejemplos en el Herbario de técnicas de ese tipo de análisis estadísticos.
Ajustar es ver hasta qué punto hay proximidad entre la realidad y un modelo propuesto. Existen casos en los que basta una técnica de ajuste para poder decir que en gran parte se agota la evaluación de la validez, la evaluación de la proximidad. Esto sucede, por ejemplo, en el ajuste de unos datos a una determinada distribución. Cualquier test de bondad de ajuste a una distribución agota la validación. Al menos la validación interna. El ajuste de la distribución a esos datos. La representatividad, por ejemplo, de la campana de Gauss, como modelo poblacional, a unos datos muestrales concretos, se agota en la misma comprobación. Tiene poca complicación por la sencillez de la situación.
Sin embargo, en modelo más complejos, como el de la Regresión logística, u otro modelo de Regresión en general, la validación, el ajuste, puede evaluarse desde perspectivas distintas. Digamos que existen bastantes dimensiones desde las que abordar el nivel de validez del modelo. Y es aquí, precisamente, donde van surgiendo los diferentes conceptos que vamos a comentar a continuación. Porque una realidad compleja, como la de la modelización de unos datos a un modelo de Regresión logística, puede evaluarse desde perspectivas diferentes, desde ángulos diferentes. Son muchas, por lo tanto, las posibles miradas a hacer.
Tenemos técnicas para evaluar el ajuste. Técnicas como la razón de verosimilitud, el método Wald, etc. Son, éstas, técnicas genéricas, técnicas «todo terreno», que valen para situaciones muy distintas.
Estos métodos de ajuste genéricos son poco finos. Hacen una valoración global. Hacen, digamos, una mirada demasiado desde arriba, desde lejos. Entran poco en detalles. Por eso se han desarrollado nuevos instrumentos en este ámbito que nos han llevado a tener que matizar la noción de Ajuste. En este contexto surgen nociones como las de Discriminación, Calibración y Precisión.
Discriminación: Es una valoración de un aspecto del ajuste. El objetivo básico de una Regresión logística es establecer, dado el valor de una variable independiente, una probabilidad de si aquel individuo tendrá o no tendrá la enfermedad estudiada. Se trata de hacer una previsión en base a la asociación vista en unos datos muestrales.
Veamos las dos situaciones extremas siguientes:
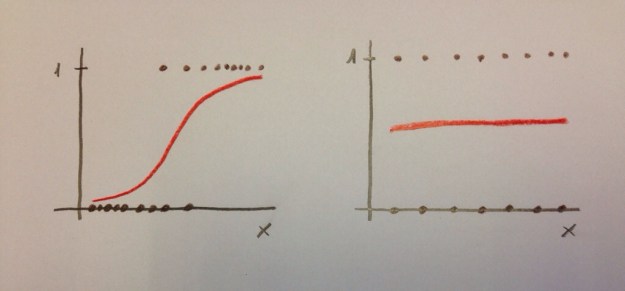
El modelo de la izquierda nos permite discriminar muy bien. Sin embargo, el modelo de la derecha no nos permite una buena discriminación. En el caso de la izquierda saber el valor de la variable «x» nos permite hacer una buena predicción de la variable dependiente. Ese valor discrimina. En el caso de la derecha el saber el valor de la variable «x» no nos informa. No discrimina.
Es muy habitual evaluar la Discriminación de un modelo de Regresión logística mediante curvas ROC y mediante el Área bajo la curva. Ver el Tema 23: Análisis ROC.
Calibración: Es otra valoración de un aspecto del ajuste. Se trata de evaluar que no haya saltos importantes entre valores observados y valores esperados, entre probabilidades observadas y probabilidades esperadas. Se trata de ver si hay paralelismos entre valores observados y valores esperados en distintos tramos de la variable independiente. Una forma habitual de evaluación de la calibración en Regresión logística es el Test de Hosmer-Lemeshow. Este Test evalúa el equilibrio entre los valores observados y los valores esperados por tramos del modelo. Si en estos diferentes intervalos se mantiene un equilibrio entre el observado y el esperado es que el modelo está calibrado.
Es importante distinguir entre Discriminación y Calibración. Porque podemos tener un modelo con buena calibración pero mala discriminación y podemos tener, también, por el contrario, un modelo con bastante buena discriminación y muy mala calibración. Veamos las dos siguientes situaciones:
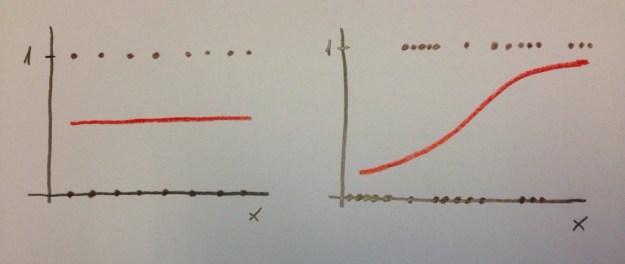
En el caso de la izquierda tenemos una muy buena calibración. Los esperados y los esperados van a coincidir perfectamente, pero la discriminación es inexistente. En el caso de la derecha sucede justo lo contrario: tenemos una aceptable discriminación pero la calibración es mala. En distintas zonas de la variable independiente los valores observados y los esperados van a tener amplias diferencias. Lo que indica que el modelo no está bien calibrado.
La Calibración tiene este problema. Que valora digamos el equilibrio en la disposición por un lado de las probabilidades según el modelo y los valores reales, que serán, evidentemente, ó 1 ó 0. La realidad, sólo da esos valores, el modelo da probabilidades. Para penetrar mejor en el ajuste, para mirar con más precisión, con una lente más potente, hay que introducir la noción de Precisión.
Precisión: Es una cuantificación del grado de aproximación de estos observados y esperados en un modelo. Es, de hecho, un complemento a la Calibración ofrecida de forma original por el Test de Hosmer-Lemeshow. El Score de Brier es uno de esos cuantificadores de la Precisión. Es un cálculo que evalúa, no por sectores, por intervalos, sino valor a valor, la distancia entre los valores observados (1 ó 0, evidentemente) y la probabilidad asignada por el modelo. Este Score, por lo tanto, no evalúa el equilibrio de observados y esperados por sectores, por intervalos, sino que evalúa distancias entre valores observados y probabilidades esperadas bajo el modelo.
El Score de Brier es el siguiente cálculo:
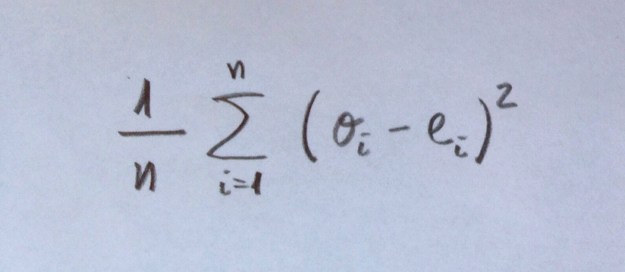
En cada uno de los n valores muestrales se resta cada observado (0 ó 1) del valor esperado que es el valor de la función dibujada en rojo para cada punto.
Observemos cómo el cálculo de este Score de Brier nos dará valores bien distintos entre las dos siguientes modelizaciones:

Estos dos modelos, si atendemos puramente a la Calibración evaluada mediante, por ejemplo, el Test de Hosmer-Lemeshow, son dos modelos calibrados. Porque si observamos diferentes intervalos de la variable independiente «x», los valores observados y esperados están muy próximos. Sin embargo, para el Score de Brier los valores serían muy diferentes. En el caso de la izquierda todos los valores esperados serían 0.5 y los observados serían 0 ó 1, lo que daría restas muy grandes. Sin embargo, a la derecha veamos que las probabilidades de los puntos con valores bajos de la variable «x» darían probabilidades muy pequeñas (porque el valor de la curva roja, la curva de la Regresión logística, nos da probabilidades de ser 1) y como en este espacio los observados son 0 esas restas darán valores pequeños. Cuando la variable «x» tenga valores grandes las probabilidades serán próximas a 1 y los valores observados serán 1, lo que nos dará, de nuevo, restas pequeñas.
Por lo tanto, el Score de Brier nos mide la precisión, la proximidad entre los pronósticos y los valores reales evaluado puntualmente; o sea, valor a valor, no intervalo a intervalo como hace la Calibración.
La Discriminación, Calibración y Precisión son, como puede verse, distintos criterios de ajuste. Es bueno que se den las tres cosas: Que el modelo discrimine bien, que esté bien calibrado y que sea preciso. Por eso es necesario evaluar cosas diferentes. Con una única evaluación nos podríamos encontrar con una deficiente evaluación.
Cuando el Ajuste, la Discriminación, la Calibración o la Precisión la evaluamos con la propia muestra utilizada para construir el modelo estamos haciendo una Validación interna.
Cuando el Ajuste, la Discriminación, la Calibración o la Precisión la evaluamos con una muestra diferente a la utilizada para construir el modelo estamos haciendo una Validación externa. El grado de alejamiento de esta muestra diferente, respecto a la muestra original, nos lleva a dos ámbitos de la Validación externa que ahora vamos a delimitar: la Reproducibilidad y la Transportabilidad.
Reproducibilidad: Con este concepto evaluamos el grado de validez de un modelo a la hora de ser aplicados a una muestra que no es la tomada para construir el modelo. Pero, eso sí, se trata de una muestra tomada en un contexto análogo al de la muestra original. Supongamos, por ejemplo, que la muestra base ha sido tomada entre pacientes de un hospital de una determinada ciudad. Pues, si lo ensayamos con pacientes de otro hospital de un nivel análogo al anterior, y de la misma ciudad, estaremos evaluando el grado de Reproducibilidad de nuestro modelo.
Una forma habitual de Reproducibilidad es hacer lo que suele denominarse una Validación cruzada (Cross-Validation). Consiste en crear, en una muestra, un subgrupo para construir el modelo y otro subgrupo distinto para validar el modelo construido. Suele hacerse diversas veces este procedimiento, en una misma muestra. Suele, entonces, denominarse una Validación cruzada con k iteraciones (k-fold Cross-Validation). Este procedimiento consiste en dividir la muestra en k subgrupos. Entonces se realiza k veces esta operación de construir el modelo con un subgrupo y validarlo con otro subgrupo. Cada una de estas veces es uno de esos k grupos el usado como grupo de validación y el resto de valores de la muestra es usado para construir el modelo.
El bootstrap es una forma habitual de trabajar a este nivel. El bootstrap es un procedimiento que genera submuestras a partir de la muestra. Una muestra es transformada en población y de ella, aleatoriamente se toman muestras del tamaño deseado.
Observemos que en cualquiera de estos procedimientos comentados nos estamos moviendo dentro de un mismo ámbito. Estamos intentando ver si la modelización hechas con una muestra sigue siendo válido con una muestra distinta aunque tomada en el mismo contexto que la muestra con la que se ha construido el modelo.
Transportabilidad: Con este concepto evaluamos, ahora, el grado de validez, el grado de proximidad, de un modelo, con todas las dimensiones vistas (Ajuste, Discriminación, Calibración, Precisión), a la hora de ser aplicado a un grupo de individuos distinto al grupo base del estudio. Ahora es otro país, otro ámbito distinto, la fuente de la muestra. Es, pues, un grado superior de generalización que el ofrecido por la Reproducibilidad.
Ahora estamos buscando el grado de inferencia a distancia: una distancia que puede ser temporal, territorial, etc.
En la Reproducibilidad y la Transportabilidad hay grados diferentes. Es un continuo. Y es de elevada complejidad saber el nivel de generalización en el que podemos situar una determinada Validación externa.
El siguiente cuadro puede constituir un resumen de todo lo visto:
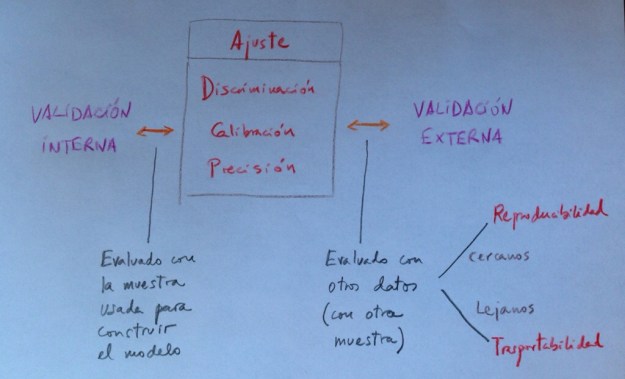
Obsérvese que este esquema intenta plantear una visión global de todo lo visto.
Los siguientes puntos resumen, también, todo lo dicho:
1. La Validación es la búsqueda del grado de proximidad entre modelo y realidad.
2. La Validación puede ser interna (si se evalúa la proximidad entre el modelo construido y los propios datos empleados para construir el modelo) o externa (si se evalúa la proximidad entre el modelo y otros datos que no sean los usados para su construcción).
3. Ajuste, Discriminación, Calibración y Precisión son distintas miradas, distintas perspectivas desde donde evaluar la Validación. Por lo tanto, son herramientas con las que valorar el grado de proximidad entre modelo y realidad.
4. Ajuste, Discriminación, Calibración y Precisión son aplicables tanto en la Validación interna como en la Validación externa. La diferencia entre estos dos tipos de Validación está en qué datos son los usados para evaluar la proximidad, pero las técnicas para hacerlo son exactamente las mismas.
5. La Validación interna es una: la evaluación de la proximidad entre realidad y modelo sólo se realiza con la muestra que se ha usado para estimar el modelo. La Validación externa, por el contrario, es mucho más compleja y multidimensional: se han propuesto distintas formas para hacerla, según sea esa otra muestra usada para el ajuste. Es por eso que se habla de la Reproducibilidad y de la Transportabilidad, incluso de distintos tipos dentro de ellos, lo que le dota de un carácter más controvertido y complejo.