Se ha publicado un muy interesante estudio, en Enero de 2014, sobre los factores de riesgo asociados a un accidente de automóvil.

El estudio lo ha publicado la revista «The New England Journal of Medicine». Y es un estudio ciertamente original. La metodología seguida es muy interesante.

El abstract del artículo es el siguiente:

Se ha puesto cámaras en el automóvil de conductores expertos y de conductores con poca experiencia. Cámaras que registraban comportamientos en el interior del vehículo. De esta forma se ha podido analizar diferentes factores y su asociación con el accidente.

Es sorprendente y didácticamente muy útil este artículo. En primer lugar por ser una forma de analizar una situación importante y hacerlo de una forma que realmente permite cuantificar un riesgo en su medida real. Todos sabemos que buscar el móvil conduciendo es un riesgo de accidente. La ventaja es que ahora lo tenemos cuantificado. Pero, por otro lado, este artículo es un paradigma de lo que es la investigación médica en el ámbito clínico. En clínica buscamos factores de riesgo tratando de cuantificarlos. Buscamos si hay asociación, y, si la hay, cuánta, entre un determinado factor y tener o no una determinada enfermedad. Buscamos también asociación, en personas que tengan una determinada enfermedad, entre dos tratamientos distintos y morir o no antes de salir del Hospital, o morir o no al año.

Pues aquí se hace lo mismo pero los factores de riesgo analizados son buscar el móvil, comer, hablar por el móvil, etc, y el tener un accidente. Y necesitamos tener datos, para cada uno de estos factores, datos de las cuatro situaciones posibles. Por ejemplo, en el caso de la búsqueda de la relación entre la búsqueda del móvil en el interior del coche y un accidente se pueden dar las siguientes situaciones posibles: Buscar el móvil con accidente asociado. Buscar el móvil sin accidente. No buscar el móvil con accidente. No buscar el móvil sin accidente. Esquemáticamente tendríamos esto:

Obsérvese que esto es como cuando buscamos la asociación entre fumar y cáncer de pulmón. Tenemos también estas mismas cuatro situaciones. Ahora serían: Fumar y tener cáncer de pulmón. Fumar y no tener cáncer de pulmón. No fumar y tener cáncer de pulmón. No fumar y no tener cáncer de pulmón.

En este sentido este artículo puede ser una forma extraordinaria de explicar lo que se hace habitualmente en la investigación clínica a personas que trabajan en ámbitos muy diferentes.

Es interesante, también, que este artículo se haya publicado en la más prestigiosa revista de Medicina, siendo un tema -entiendo- no materialmente médico, pero sí formalmente. Es un artículo que no siendo de Medicina se ha trabajado con mirada y con los procedimientos estadísticos habituales de la Medicina.

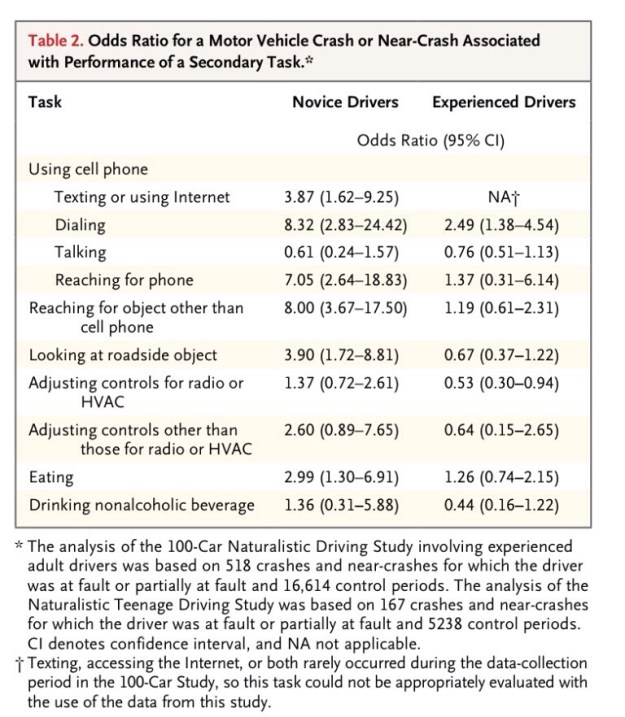
En el estudio la tabla principal de resultados es la siguiente:

Puede verse en esta tabla las Odds ratio y los intervalos de confianza obtenidos para cada uno de los factores de riesgo estudiados.

Para ver cómo se calculan estas Odds ratio y sus intervalos de confianza se puede consultar el artículo La Odds ratio y el Riesgo relativo y sus intervalos.

Por ejemplo, si tomamos el caso de buscar un móvil mientras se conduce, para el que han encontrado una Odds ratio de 7.05, podríamos tener unos datos como los siguientes:

Con estos datos, si vamos al artículo citado donde se ve cómo se realiza el cálculo de la Odds ratio, podremos comprobar que la Odds ratio sería 7. Lo que significa que se tiene 7 veces más accidentes buscando móvil que sin buscarlo: 1 respecto a 2 es 7 veces mayor que 10 respecto a 140; o sea: (1/2)/(10/140) es 7.

Sin embargo, en este caso, si calculamos el intervalo de confianza del 95% nos da un intervalo que es el siguiente: (0.58, 83.98). Como el 1 está dentro del intervalo se entiende que se trata de una Odds ratio no significativa.

Si, por el contrario, nuestros datos fueran los siguientes:

Seguiríamos teniendo una Odds ratio de 7, porque la relación es la misma porque he añadido un cero en cada celdilla, pero ahora el intervalo de confianza del 95% sería uno bien diferente: (3.19, 15.36). Ahora al no contener el 1 podemos hablar de una Odds ratio significativa y, si observamos los datos de la tabla del artículo, vemos que la amplitud del intervalo es similar a éste.