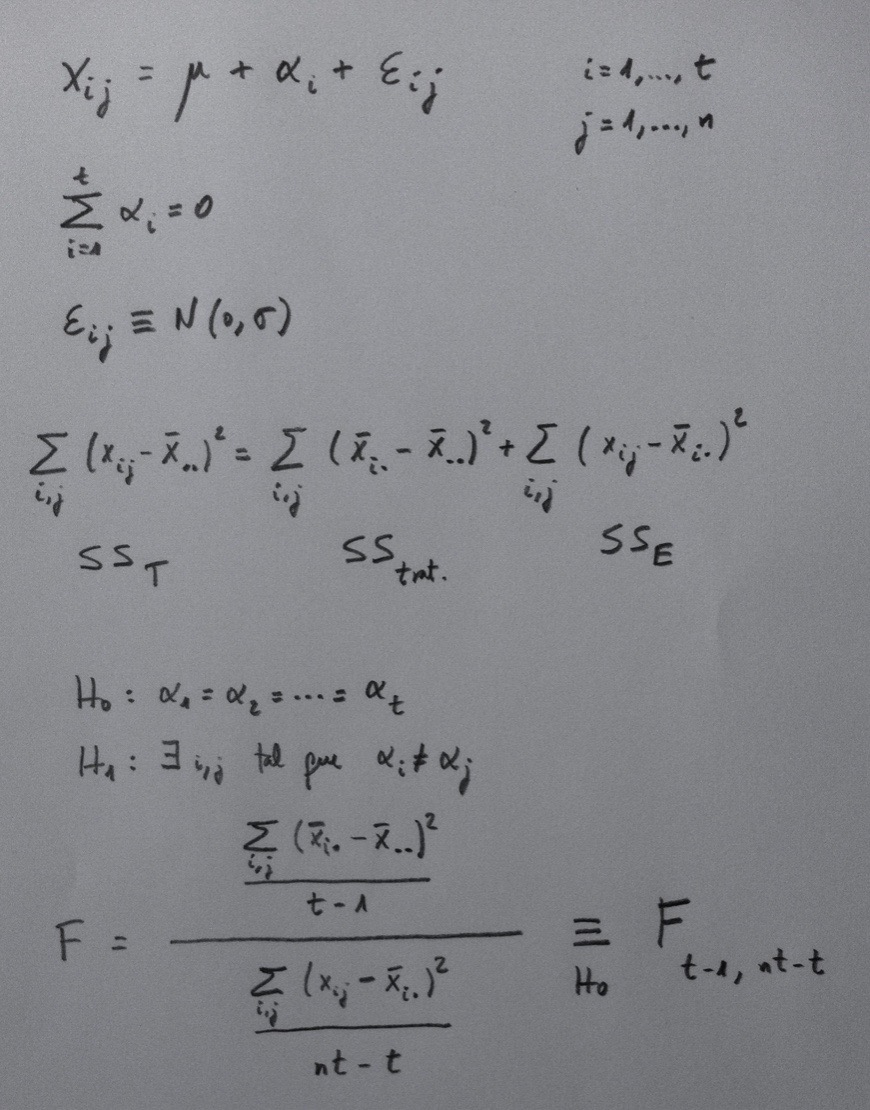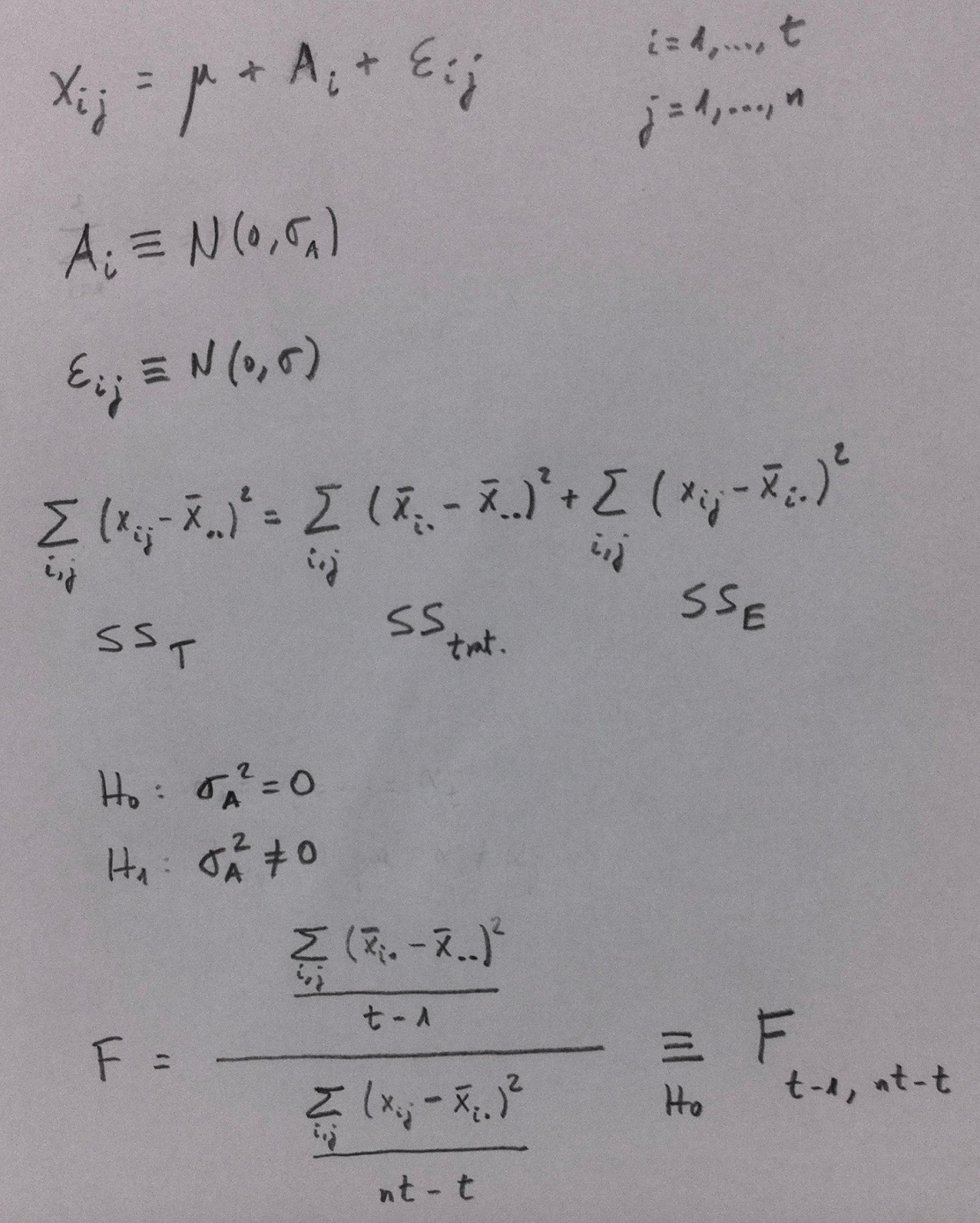El Teorema de las probabilidades totales y el Teorema de Bayes son dos teoremas clásicos en el campo de las Probabilidades que tienen muchas aplicaciones.

Parten ambos de que tenemos una partición definida en un conjunto de individuos. Esto quiere decir que un conjunto de individuos lo tenemos partido en una serie de grupos que no se tocan entre ellos; o sea, en términos matemáticos diríamos que tienen intersección vacía. Nadie, en definitiva, pertenece a más de uno de esos grupos. Y todos pertenecen a uno u otro de esos grupos.

Por ejemplo, la población de personas queda estructura en una partición según el grupo sanguíneo del sistema AB: La partición es A, B, AB y O. Respecto a una determinada patología la población siempre queda partida en un grupo formado por todos los que tienen esa patología y en otro formado por todos los que no la tienen. Esta partición veremos que en Medicina tiene mucha importancia a la hora de abordar unos conceptos esenciales en diagnóstico: la sensibilidad, la especificidad, el valor predictivo positivo y el valor predictivo negativo.

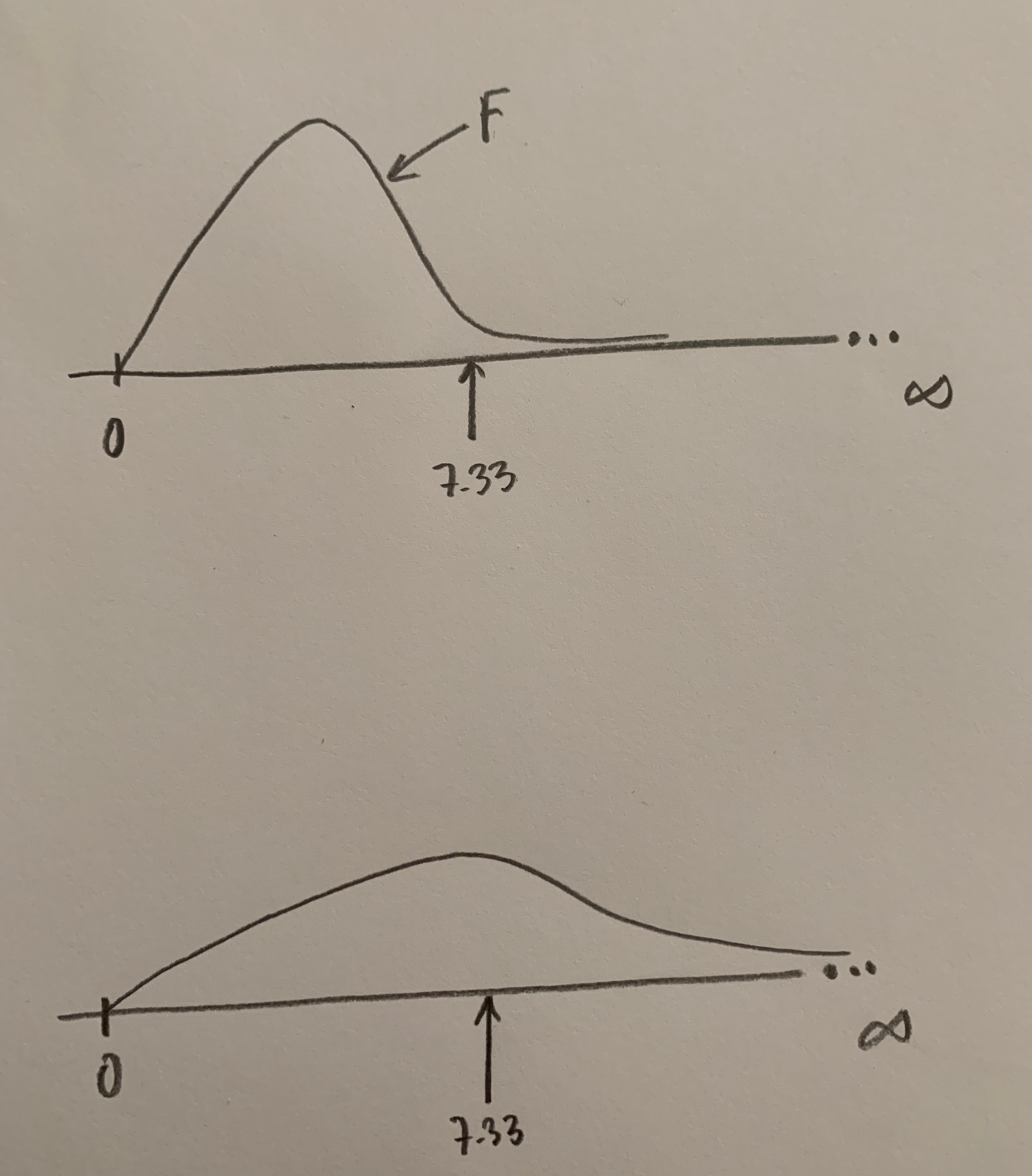
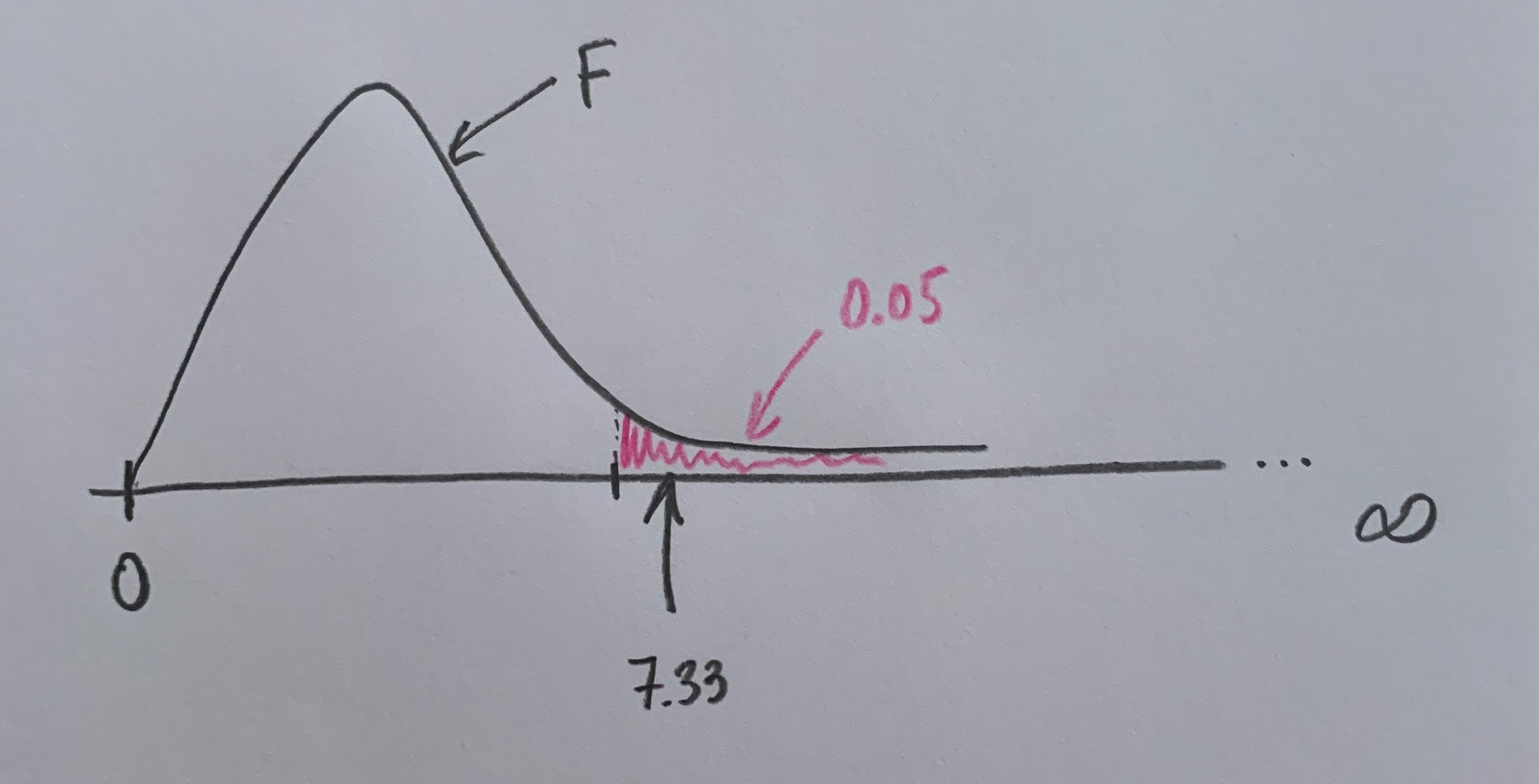
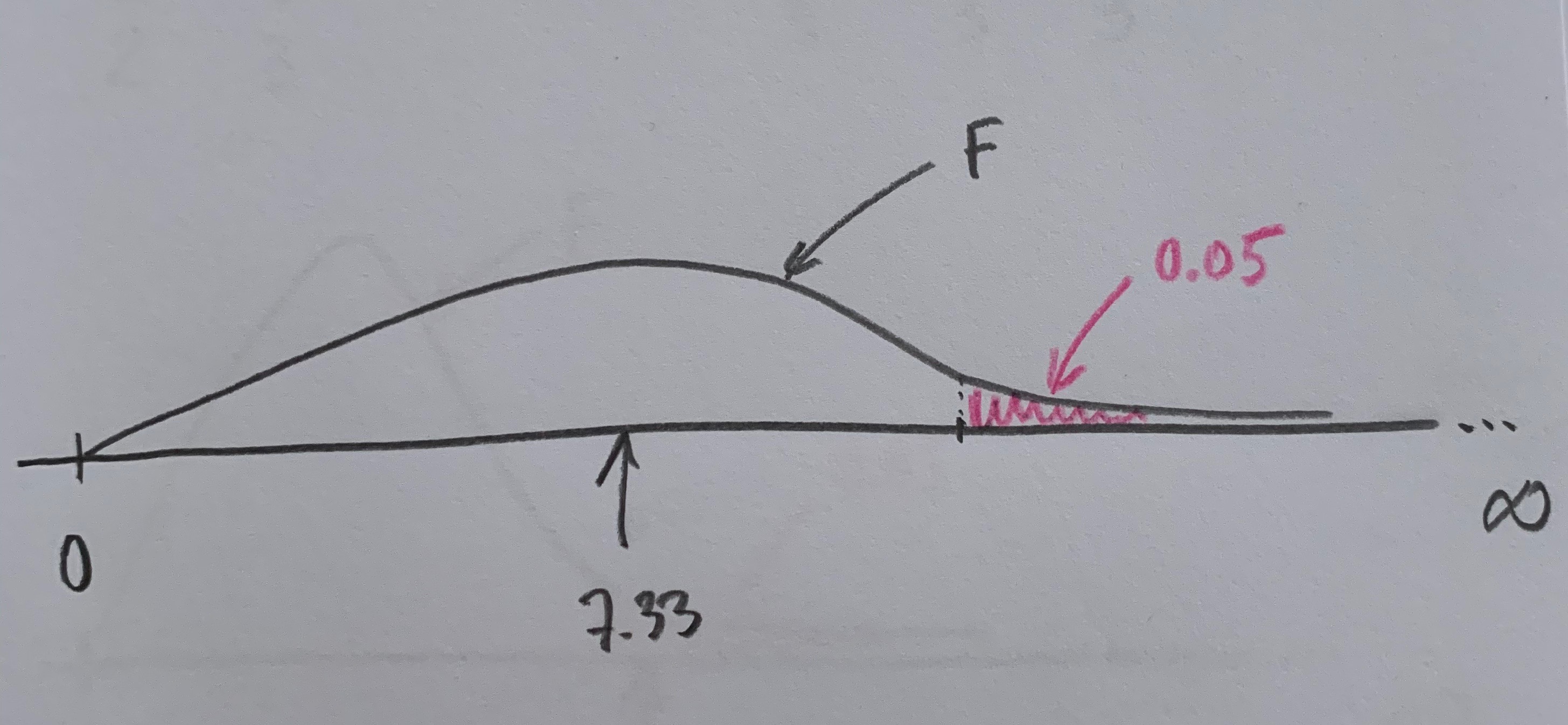
Dentro de esta partición puede definirse un conjunto, que llamaremos A, que está inmerso en ella y que se toca con todos los grupos que define tal partición. Puede darse algún caso en el que se tenga la información de la probabilidad de cada uno de los grupos de la partición y que se sepan, también, todas las probabilidad de que se dé este suceso A condicionadas a que se haya dado cualquiera de los grupos de la partición. En este caso podemos calcular la probabilidad de A mediante el Teorema de las probabilidades totales. Observemos el siguiente gráfico:

Para llegar a la formulación final del Teorema es necesario aplicar la definición de probabilidad condicionada. Es importante tener en cuenta que para poder aplicar este Teorema debemos conocer la probabilidad de cada uno de los elementos de la partición y todas las probabilidades condicionadas que nos muestra el gráfico.

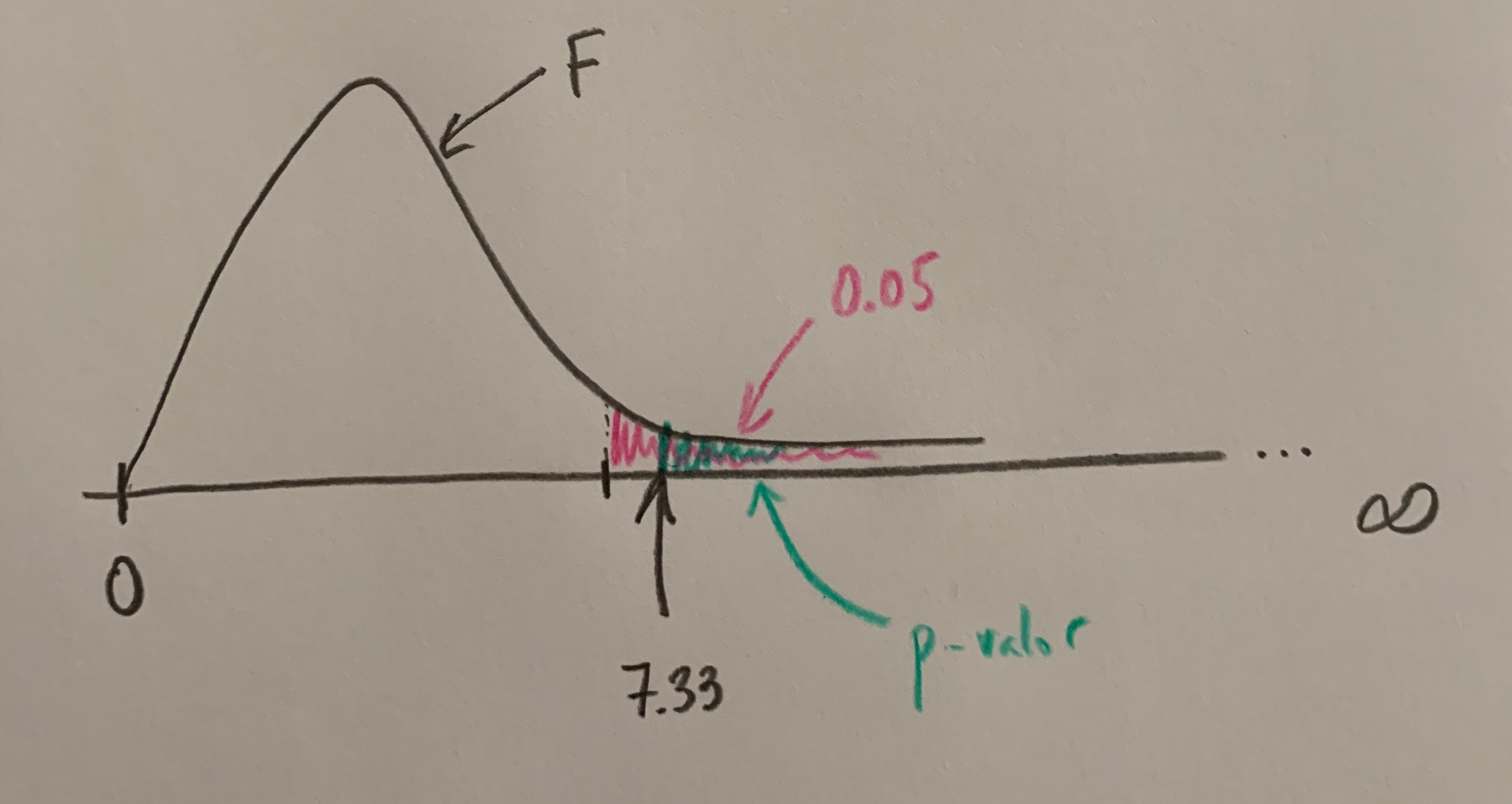
El Teorema de Bayes parte también del conocimiento de estas mismas probabilidades pero el planteamiento es otro. Sabemos que se ha producido el suceso A y nos planteamos la probabilidad de que se haya dada uno de los elementos de la partición. Veamos el planteamiento:

Un ejemplo aclarará ambos teoremas:

Supongamos que estamos estudiando una enfermedad en una población que sabemos que tiene una prevalencia de 0.3 (o, en porcentaje, del 30%). La población queda partida en dos grupos: Enfermos (E) y No enfermos (NE). La probabilidad de E es 0.3 y la de NE es 0.7. Supongamos también que podemos aplicar una técnica diagnóstica para ver si una persona tiene o no tiene esa enfermedad. Supongamos que sabemos la probabilidad de que la prueba dé positiva (+) si una persona tiene la enfermedad; o sea, la P(+/E) y que también sabemos la probabilidad de que la prueba dé positiva si una persona no tiene la enfermedad; o sea, la P(+/NE). Si quisiéramos sabe la probabilidad de que cogiendo una persona al azar en esa población la prueba diera positiva; o sea, la P(+) deberíamos aplicar el Teorema de las probabilidades totales. Si lo que nos planteáramos fuera saber que sabiendo que ha dado positiva la prueba en una persona calcular la probabilidad de que sea una persona con la enfermedad; o sea, P(E/+) deberíamos aplicar el Teorema de Bayes. Veámoslo:

De hecho, aquí, en este ejemplo, aparecen conceptos de una importancia crucial en Medicina. En cualquier procedimiento diagnóstico a la probabilidad P(+/E) se la denomina Sensibilidad, al valor 1-P(+/NE); o sea, a la P(-/NE) se le denomina Especificidad. Y a la probabilidad P(E/+) se le denomina Valor predictivo positivo. Ver el artículo «Sensibilidad, Especificidad, Valor predictivo positivo, Valor predictivo negativo» del apartado de Estadística y Medicina.

La noción de probabilidad es conceptualmente muy sencilla. Se trata del siguiente cociente:

Tan sencillo como esto. Entre todas las posibilidades cuáles son las favorables. Si queremos saber la probabilidad del 1 en un dado es 1/6 porque aplicamos este cociente. Si queremos saber la probalidad de cara en el lanzamiento de una moneda es 1/2 porque también aplicamos este cociente.

La noción de probabilidad condicionada es también muy importante conocerla porque muchas veces tenemos información ante la incertidumbre de un determinado suceso. Y no es lo mismo P(A) que P(A/B). No es lo mismo preguntarse por la probabilidad de A, sin más, que la probabilidad de A sabiendo que se ha producido el suceso B. Veamos esta noción:

Al saber que se ha producido el suceso B las cosas cambian, el campo de lo posible cambia. Si antes potencialmente todo era posible ahora sólo es posible que suceda algo dentro de B. Por eso, en general, cambia la probabilidad de A al saber que ha sucedido B.

Si la probabilidad de A no cambia al saber que ha sucedido B; o sea, que P(A/B)=P(A), entonces decimos que los sucesos A y B son independientes. Y, por lo tanto, en este caso, a partir de la fórmula de la probabilidad condicionada llegamos a la siguiente importante igualdad:

El elemento clave en ANOVA, y de aquí su nombre, es la descomposición de la variabilidad global o total, en diferentes fuentes de variabilidad. Análisis de la varianza viene de ahí, analizar es descomponer una unidad en sus diferentes elementos constitutivos.

En todo modelo ANOVA hay siempre una descomposición de la variabilidad.

En un ANOVA de un factor es:

En una ANOVA de dos factores cruzados la descomposición es:

Las diferentes medias las podemo ver en el siguiente esquema:

Veamos el papel de la interacción en los dos ejemplos siguientes:

Supongamos un experimento en el que tenemos un único factor y muchos niveles. Decidimos coger una muestra de niveles y en cada uno de esos niveles elegidos tomamos una muestra. Por ejemplo, queremos ver si la contaminación en diferentes cincuenta ríos de España es diferente significativamente. Otro ejemplo, queremos ver, en una empresa donde trabajan cien empleador elaborando un producto, si hay diferencia entre ellos.

Supongamos que cogemos una muestra de tres niveles y los valores obtenidos son los siguientes:

Si aplicamos un modelo de ANOVA de un factor a efectos aleatorios la tabla ANOVA y las componentes de la varianza son:

Hay diferencias estadísticamente significativas. El p-valor es 0.003. Aquí no tiene sentido aplicar unas comparaciones múltiples porque no son esos tres niveles los que nos interesan, sino toda la población de niveles (los cincuenta ríos en el primer estudio y los cien trabajadores en el segundo). Por eso evaluamos la componente de la varianza de nuestro factor, que es 3,7. Este valor sale del siguiente cálculo:

El estadístico Cuadrado Medio del factor tiene un promedio, como variable que es. Es la denominada Esperanza del cuadrado medio. Esto lo veremos con más detalle en modelos más complejos. A partir de este valor promedio construimos una estimación de la componente de la varianza de nuestro factor aletorio:

Observemos que el valor de 3.7 para la componente de la varianza se obtiene de restar 20.6 y 2.1 y dividir luego por 5, que es el tamaño de cada muestra.

Todo modelo tiene siempre una componente de la varianza, que es la residual. Que se puede obtener del valor de Cuadrado medio residual, como se puede ver en la Tabla ANOVA.

 

El Análisis de la varianza (ANOVA) es una familia de técnicas estadísticas de comparación. El objetivo de esas técnicas es decidir si hay igualdad o diferencia entre poblaciones a partir del análisis de muestras de esas poblaciones.

Nos podemos encontrar con cosas como las siguientes. Veremos a continuación tres situaciones distintas donde se están comparando, en cada una de ellas, tres muestras de tres poblaciones. Si observamos un poco atentamente nos encontraremos con situaciones bien distintas que llevan a intuiciones muy distintas acerca de cómo deben ser las poblaciones que hay detrás de esas muestras:

En el primer caso parece claro que la muestra tres presenta valores superiores y la muestra segunda valores inferiores.

En el segundo caso parece que estas tres muestras se solapan mucho. Lo que hace pensar que, con la información que tenemos, no podemos decir con fiabilidad que las poblaciones que hay detrás son distintas.

En el tercer caso parece que la muestra tres tiene valores superiores y, sin embargo, la uno y la dos son muy similares.

De esto va el ANOVA, de tomar decisiones sobre situaciones de este tipo.

El problema es que a la hora de tomar esa decisión debemos analizar siempre, como veremos, tres dimensiones fundamentales. Tres dimensiones que se solapan, que se entremezclan. Son las siguientes: las distancias entre las medias de esas muestras, las dispersiones internas de cada muestra y el tamaño de muestra.

Veamos esas tres dimensiones individualmente.

Primero: La posición relativa de esas medias. Miremos estas tres distintas situaciones, donde representamos los valores de las muestras con una cruz en la posición que ocupan en la recta numérica:

Cuanto más alejados estén los valores medios (señalados con una línea perpendicular a la recta de números) de las muestras  a comparar más posibilidades tenemos de que podamos decir que hay diferencias entre las poblaciones.

En el primer caso vemos que la muestra roja y azul están muy solapadas y la verde se aleja considerablemente. En el segundo caso hay un grado de solapamiento muy grande, las medias están muy cerca. En el tercer caso hay una clara distancia entre medias.

Pero observemos que en estos tres casos, a la hora de evaluar las distancias entre las medias vemos inevitablemente cuál es el grado de solapamiento de las muestras de las poblaciones que comparamos. Esto nos lleva a la segunda dimensión:

Vemos en estos dos casos que las distancias entre las medias de estas tres muestras son las mismas en el primer estudio y en el segundo pero, sin embargo, lo que podamos decir de las poblaciones que hay detrás, es completamente distinto. En el primero no podemos decir que hay diferencias, en el segundo parece fiable que podemos decir que hay diferencias.

La dispersión de los valores es, pues, esencial a la hora de evaluar las diferencias.

Y, como tercera dimensión, en ANOVA, tenemos el tamaño de muestra:

De nuevo en estos dos casos las distancias entre medias son las mismas, el grado de solapamiento equivalente. Lo que es distinto es claramente el tamaño de muestra. Cuanto más tamaño de muestra tengamos más fiables son las distancias muestrales que estemos viendo.

En un caso concreto, cualquiera de las técnicas ANOVA debe evaluar esas tres dimensiones (distancia entre medias, dispersión interna de las muestras y tamaño de muestra) para poder tomar una decisión sobre si las poblaciones son iguales o son distintas.

Veamos un caso concreto:

Aquí tenemos cinco muestras, con un tamaño muestral determinado, unas dispersiones determinadas, unas distancias entre medias. Aquí parece que habrá diferencias y que habra como tres grupos de poblaciones: la roja y la azul por un lado, la verde y marrón por otro y la de color granate, a la derecha, como tercer grupo.

El el Herbario de técnicas de este blog tenemos diferentes modelos ANOVA. Todos ellos muestran su parametrización. Vamos a ver aquí el concepto de parametrización. Veamos el ejemplo más sencillo: ANOVA de un factor a efectos fijos:

Un valor cualquiera de un experimento lo podemos descomponer en tres. En los modelos ANOVA más complejos esta descomposición se hará en muchos más elementos.

Veamos por qué se hace esto y qué representa. Se hace para ver diferentes fuentes de variación y así poder realizar los contrastes de hipótesis oportunos. Qué representa. Veamos el siguiente caso: Un experimento con un factor a tres niveles con tres valores muestrales en cada nivel:

La media global es 3 y la media de cada uno de los tres niveles es: 2, 3, y 4, respectivamente.

Vamos a ver cómo hacemos la descomposición:

Primer paso:

Hemos expresado cada uno de los nueve valores muestrales como iguales a la media global, que es la letra griega mu de la parametrización. Pero con esto no tenemos una verdadera igualdad.

Segundo paso:

Hemos añadido para cada valor un valor característica del grupo, de aquella muestra a la que pertenece. Que es la alfa de la parametrización. Pero las alfas son diferentes según el grupo. La alfa es de hecho la diferencia de la media del grupo respecto a la media global. Es, pues, un valor de alejamiento promedio de los diferentes miembros de aquel grupo, de aquella muestra, respecto del valor promedio global. En este casos son: -1, 0 y 1. Pero veamos que todavía no tenemos igualdades ciertas.

Tercer paso:

Ahora hemos añadido el elemento que falta para satisfacer la igualdad. Con ello aportamos un valor individual. Es la épsilon del modelo.

En nuestro caso estas épsilons, estos valores individuales son siempre valores repetidos, pero porque se trata de un ejemplo artificial hecho con mucha simetría de valores para que se pueda entender bien pero en general estos valores individuales serán números distintos para cada caso.

Este es el sentido de la parametrización. Descomponer cada valor muestral de nuestro estudios en distintos valores. De esta forma conseguimos crear distintas fuentes de variación que serán claves a la hora de realizar los contrastes de hipótesis; o sea, a la hora de evaluar efectos, a la hora de tomar decisiones en ANOVA.

 

 

 

Hemos visto cómo funciona la parametrización de un ANOVA de un factor. Los dos casos posible: factor fijo y factor aleatorio, son los siguientes:

La hipótesis nula es, en ambos, igualdad y la alternativa no igualdad. Se interpreta distinto porque como ya hemos visto en otro lugar, en el factor fijo estamos comparando unos niveles que expresamente nos interesa comparar y en el factor aleatorio tenemos una muestra de niveles, y, por lo tanto, lo que nos interesa es hablar de la igualdad o no entre muchos niveles que no tenemos. Por eso aparece, en este caso, una estimación de la varianza que hay entre esos niveles, la denominada componente de la varianza.

Vamos a ver cómo funciona el contraste de hipótesis.

Vamos a situarnos en las dos situaciones posibles más extremas. Supongamos los dos experimientos siguientes:

Si calculamos el estadístico de test F en el experimento de la izquierda toda la variabilidad está en el numerador y en el denominador tenemos un valor claramente de 0. Por lo tanto, el valor de la F es infinito. En el experimiento de la derecha toda la variabilidad está en el denominador y el numerador es 0. Por lo tanto, tenemos las dos situaciones extremas posibles: En el experimiento 1 la hiótesis nula de igualdad de poblaciones es absurdo quererla mantener y en el experimento 2 lo que es absurdo es rechazar la hipósis nula; o sea, decir que hay diferencias cuando las tres muestras de esas tres poblaciones son idénticas.

Las posibilidades son pues las extremas:

Pero lo cierto es que los estudios de ANOVA de un factor prácticamente siempre tendremos valores que no serán ninguno de estos dos valores extremos. Por ejemplo, tendremos el valor siguiente:

¿Qué decisión tenemos que tomar con un valor de F de 7.33? Si el valor está próximo al 0 mantendremos la Hipótesis nula si es próximo al infinito rechazaremos la Hipótesis nula y abrazaremos la Hipótesis alternativa. Pero, ¿dónde situamos el umbral para la toma de esta crucial decisión?

Aquí está el problema. Lo que hizo Fisher es, partiendo de unas suposiciones (valores independientes, con distribución normal y con igualdad de varianzas de cada muestra), ver cuál sería la variabilidad, la distribución de los valores posibles de este cálculo F, si fuese cierta la Hipótesis nula. Y así fue como definió, estudió y tabuló la denominada distribución F de Fisher.

Fijaos que si dibujamos la forma de cómo deberían ser las cosas si fuese cierta la Hipótesis nula este valor de 7.33, o el que tuviésemos en un estudio concreto, adquiere sentido, te permite decantarte por una hipótesis u otra con más sentido.

Mirad el dibujo:

Este 7.33, que antes no sabíamos cómo interpretar ahora sí parece tener sentido. Arriba podemos decir que estamos viendo algo muy poco probable si fuese cierta la Hipótesis nula y, en cambio, debajo podemos decir que estamos viendo algo muy probable si fuese cierta esa Hipótesis nula de igualdad de poblaciones, o de ausencia de efectos.

Observemos que si fijamos una área de poca probabilidad bajo el supuesto de ser cierta la Hipótesis nula, tendríamos los dos siguientes dibujos:

Se crea así un umbral para la toma de decisión. Si se supera se rechaza la Hipótesis nula, si no se supera se mantiene esa Hipótesis. En el primer caso hemos superado el umbra, en el segundo no. Ahora, pues, el 7.33 nos permite tomar una decisión. Suele establecerse un umbral con probabilidad baja en la zona de influencia más alejada de la Hipótesis nula, que es el extremo derecho.

Actualmente lo que hacen los softwares estadísticos es calcular el llamado p-valor, que es el área que hay a la derecha, hacia la zona más alejada de la coherencia de la Hipótesis nula, desde el punto del valor de la F calculada a las muestras del estudio:

Si este p-valor es menor que 0.05 es que el valor de la F calculada está a la derecha del umbral de tolerancia para mantener la Hipótesis nula. Si este p-valor es mayor que 0.05 es que ese valor de la F calculado a la muestra está a la izquierda del umbral, está en zona donde es coherente lo que vemos con la hipótesis de igualda o de no efectos, de no diferencias entre los niveles comparados (si es un factor fijo) o de varianza cero de los niveles poblacionales compardos (si es un factor aleatorio).

La distribución F de Fisher tiene, como se ve formas distintas, siguiendo siempre ese patrón que se ve dibujado en estos gráficos. La concreta forma que tenga va a depender del número de niveles del factor y del tamaño de muestra que estemos estudiando en global:

Tiene dos parámetros y el primero es t-1, el número de niveles del estudio menos uno, y el segundo parámetro es el número de observaciones totales (nt) menos el numero de niveles; o sea, nt-t.

Y el umbral lo obtenemos de unas tablas como esta:

En las columnas encontramos el valor del primer parámetro y en las filas el del segundo parámetro.

Por ejemplo: supongamos que estamos comparando tres niveles de un factor y tenemos tres valores por cada nivel, como en los ejemplos ficticios de antes. Entonces t-1 sería 2 porque tenemos tres niveles y nt-t sería 8, porque, como la n es 3 y la t también 3, la F sería una F(2,6), que es como también se suele escribir. El valor umbral sería, mirando la tabla, el valor de 5.14. Este valor sería el valor que nos permitiría, dados unos datos concretos, tomar una decisión según el valor de la F fuera menor o mayor que este umbral.

 

 

 

 

Uno de los objetivos fundamentales de la Ciencia es tomar decisiones. Decisiones acerca de cómo debe de ser lo que no vemos (lo poblacional) a partir de la información que extraemos de lo que vemos (la muestra). El contraste de hipótesis estadístico es el principal método mediante el cual se toman esas decisiones en la Ciencia.

En todo contraste de hipótesis el patrón de funcionamiento es siempre el mismo. Es muy importante captar esta idea si se quiere comprender la Estadística y, también, la Ciencia. Karl Pearson decía que la Estadística es la gramática de la Ciencia. Seguramente es en el contraste de hipótesis donde podemos ver mejor los elementos nucleares de esa gramática.

Hay tres elementos básicos en la toma de la decisión:

1. La diferencia entre el valor muestral y el valor poblacional establecido en la Hipótesis nula. La distancia que hay entre lo que vemos muestralmente y lo que afirmamos sobre la población, en definitiva.
2. La dispersión que tengamos en la muestra. La variabilidad, lo alejados que estén los valores respecto de la media. La imprevisibilidad, por lo tanto, de los valores que podemos tener.
3. El tamaño de muestra que tengamos. La cantidad de información que tenemos de la inmensa población sobre la que queremos hablar.

El esquema general en el que relacionamos estos tres factores es siempre el siguiente:

En definitiva, en un contraste de hipótesis, se trata de ver cuán diferente es el cálculo muestral respecto al que se afirma, poblacionalmente, en la Hipótesis nula, que es lo que calculamos en el numerador. Cuanto más próxima a 0 sea esa diferencia más coherente será mantener esa Hipótesis nula. Observemos que el numerador marca la distancia absoluta entre el cálculo muestral y la hipótesis sobre cómo es la población que no tengo.

Sin embargo, este cálculo del numerador que valora la distancia entre lo que veo y lo que afirmo sobre la población quedará matizado por la dispersión y por el tamaño de muestra que tengamos. Observemos bien el cociente: En el denominador tenemos un cociente entre la dispersión y el tamaño de muestra.

Si la dispersión es grande esa diferencia se verá disminuida, si esa dispersión es pequeña esa diferencia entre el valor muestral y el poblacional se verá aumentada.

Lo contrario sucede con el tamaño de muestra: si es grande el tamaño muestral esa diferencia calculada en el numerador se verá aumentada (porque al ser grande el tamaño de muestra el cociente entre la dispersión y el tamaño de muestra se hace pequeña) y si el tamaño de muestra es pequeño esa diferencia se verá disminuida (porque al ser pequeño el tamaño de muestra el cociente entre la dispersión y el tamaño de muestra se hace grande).

Cuanto más próximo a 0 sea este cociente más razonable será mantener la Hipótesis nula y, por el contrario, cuanto más alejado esté de 0 más coherente será rechazarla y pasar a la Hipótesis alternativa.

Veamos estos tres factores cómo influyen para que el cociente sea próximo a 0 ó, por el contrario, sea un valor alejado del cero:

Valores pequeños de diferencia, grandes de dispersión y pequeños de tamaño de muestra hacen que el cociente sea pequeño. Valores grandes de diferencia, pequeños de dispersión y grandes de tamaño de muestra hacen que el cociente se haga grande.

Cada contraste tendrá un umbral para hacer este paso de la Hipótesis nula a la alternativa. El umbral será ese valor que ya hace intolerable la distancia entre lo que vemos y lo que afirmamos en la Hipótesis nula sobre la población.

El p-valor, de hecho, es una forma estandarizada de evaluar este alejamiento del cero. Cuanto menor es el p-valor más alejado estamos del 0 y cuanto más próximo a 1 sea el p-valor más cerca del 0 estamos en este cociente. De hecho, si el valor de la  muestra coincide con el valor poblacional de la Hipótesis nula el p-valor será 1. ¿Hay en esta situación algún argumento coherente para rechazar esa hipótesis?

La frontera del 0.05 en el p-valor es la expresión estandarizada de que estamos justo sobre el umbral de tolerancia del mantenimiento de la Hipótesis nula.

Veamos en los siguientes cinco ejemplos de contrastes de hipótesis: Contraste sobre la correlación de Pearson, Contraste de una proporción, Contraste de comparación de proporciones, Contraste de una media y Contraste de comparación de medias:

Obsérvese que siempre estamos haciendo un cociente como el que hemos escrito antes, conceptualmente, un cociente entre la diferencia entre lo muestral y lo que afirmamos poblacionalmente en la Hipótesis nula y el valor de otro cociente: el que hay entre la dispersión y el tamaño de muestra que tenemos.

A la derecha de cada cociente tenemos la distribución de ese cociente en el caso de que fuera cierta la Hipótesis nula, que es lo que nos permite fijar un umbral o calcular un p-valor como criterio para decidir si mantenemos la Hipótesis nula o, por el contrario, la rechazamos y nos quedamos con la Hipótesis alternativa.

Tenemos la siguiente base de datos de pacientes con demencias diagnosticadas:

Variables:

P=Paciente

S=Sexo (h=hombre; m=mujer)

E=Edad

EVC=Enfermedad vascular central (s=sí; n=no)

EVP=Enfermedad vascular periférica (s=sí; n=no)

D=Diabetes (s=sí; n=no)

MM0=Mini Mental en el diagnóstico

MM3=Mini Mental a los 3 años

MM5=Mini Mental a los 5 años

P	S	E	EVC	EVP	D	MM0	MM3	MM5
1	h	60	s	n	n	21	20	18
2	h	79	n	n	n	20	19	16
3	h	71	n	s	s	23	20	17
4	h	66	n	s	s	22	19	16
5	m	69	n	n	s	21	19	16
6	m	62	n	n	s	24	22	19
7	m	60	s	n	n	21	19	16
8	m	63	s	n	n	24	22	19
9	m	77	n	s	n	23	21	18
10	h	63	n	s	n	20	18	15
11	h	79	n	s	n	24	22	19
12	h	55	n	s	s	23	21	18
13	m	72	n	n	s	21	19	16
14	m	68	n	n	n	21	21	20
15	h	81	n	n	s	23	21	18
16	h	71	n	n	n	20	19	19
17	m	61	n	s	s	24	23	20
18	m	76	s	s	s	23	22	19
19	m	72	s	s	n	22	21	18
20	m	63	n	n	n	24	23	20
21	m	67	n	n	n	21	20	17
22	h	69	n	n	n	23	22	19
23	h	60	n	n	n	21	20	17
24	m	64	n	n	s	22	21	18
25	m	73	n	n	s	21	20	17
26	m	66	s	n	n	23	21	18
27	m	76	s	n	n	22	20	17
28	h	75	n	n	n	23	21	18
29	m	62	n	n	s	21	19	16
30	m	78	n	n	n	24	22	19
31	h	57	n	s	s	23	21	18
32	h	58	n	s	s	21	19	16
33	m	63	s	s	n	23	21	18
34	m	65	n	s	n	24	22	19
35	m	74	s	s	n	20	17	14
36	m	61	n	n	n	24	22	19
37	h	71	n	n	s	23	21	18
38	m	71	n	n	n	22	21	18
39	m	63	n	n	s	24	23	20
40	h	67	n	n	s	21	20	17
41	h	69	n	n	n	21	20	17
42	m	63	n	n	n	21	20	17
43	m	75	n	s	n	22	21	18
44	m	69	n	s	n	21	20	17
45	m	62	s	s	n	24	20	17
46	m	66	s	s	s	24	20	16
47	h	57	n	s	n	23	22	19
48	h	62	n	s	s	21	18	16
49	h	59	n	n	n	21	20	17
50	m	72	n	n	s	28	27	24
51	m	78	n	n	s	24	23	20
52	m	73	s	n	n	24	23	20
53	m	63	n	n	n	23	24	21
54	h	65	s	n	n	23	22	19
55	m	67	n	s	n	23	22	21
56	m	66	n	s	n	24	23	20
57	h	75	n	n	s	22	21	18
58	h	62	n	n	n	21	20	17
59	m	71	n	n	s	23	22	19
60	m	59	s	s	n	22	17	16
61	m	66	n	n	s	24	23	20
62	m	64	n	n	s	23	22	19
63	m	65	n	n	n	22	21	18
64	h	71	n	n	n	24	23	20
65	h	68	n	n	n	21	20	17
66	h	73	n	n	n	21	20	17
67	m	64	n	n	n	21	20	17
68	m	60	s	s	s	22	18	15
69	m	76	n	n	n	21	21	18
70	m	64	n	n	s	23	23	20
71	h	68	n	n	n	22	19	16
72	m	63	n	n	s	23	19	16
73	m	68	n	n	s	21	19	16
74	h	73	n	n	n	21	22	16
75	h	62	n	n	n	23	19	16
76	m	65	n	n	n	24	23	20
77	m	76	n	n	n	20	19	16
78	m	61	n	n	n	24	23	20
79	m	67	n	n	s	22	20	17
80	m	64	n	n	n	22	21	18
81	h	64	n	n	s	23	21	18
82	m	69	n	s	s	20	17	15
83	m	74	n	n	n	22	21	20
84	m	57	n	n	n	24	23	20
85	h	67	n	n	n	23	22	19
86	h	73	n	n	n	22	21	18
87	m	74	n	n	s	21	20	17
88	m	72	s	s	n	23	20	17
89	m	78	n	n	s	24	23	20
90	m	68	s	s	s	22	20	18
91	h	73	n	n	n	21	20	17
92	m	64	n	n	n	21	20	17
93	h	75	n	n	n	23	22	19
94	h	63	n	n	n	23	23	21
95	m	79	n	n	n	20	19	16
96	m	77	s	n	s	24	20	16
97	m	76	n	n	s	23	22	19
98	m	62	n	s	n	22	21	19
99	h	70	n	n	s	24	23	21
100	m	73	n	n	s	20	20	16

A.Técnicas descriptivas:

1. Calcular la media, desviación estándar, mediana, primer y tercer cuartil, rango y rango intercuartílico de la variable MM0.
2. Hacer una estadística básica de la variable Edad (Media y desviación estándar o Mediana y rango intercuartílico).
3. Hacer un Box-Plot de la variable MM5.
4. Hacer una estadística de la variable Diabetes.

B.Técnicas de relación:

1. Calcular la correlación entre la Edad y el MM en el diagnóstico (MM0).

2. Crear una función que pronostique el MM5 a partir del MM0. Valorar la capacidad predictiva.

3. Ver si hay relación entre el sexo y el que en cinco años disminuya más de cuatro (o sea, cinco o más) puntos el MM desde el diagnóstico.

4. Calcular la Odds ratio para ver si hay riesgo o protección, cuantificándolo, entre tener algún problema de riesgo vascular (Enfermedad vascular central, periférica o diabetes) y que en cinco años disminuya más de cuatro (o sea, cinco o más) puntos el MM desde el diagnóstico.

C.Técnicas de comparación:

1. Comparar si hay diferencias estadísticamente significativas en el nivel del MM a los cinco años (MM5) entre hombre y mujeres.
2. Comparar si hay diferencias estadísticamente significativas en el nivel de diferencia entre MMO y MM5 (o sea, la caída del MM entre el diagnóstico y los 5 años desde el diagnóstico) entre los que tienen o no algún problema vascular.

 

Todo lo preparado en este fichero lo ha hecho un alumno al que quisiera agradecer mucho el trabajo realizado. Su nombre es Manel Montblanch Berga.

1. Se ha pedido si se sabía cómo afectaba la pesca de arrastre a las poblaciones de Horsea a 50 estudiantes de Submarinismo y 50 Entrenadores Pokemon. La muestra se ha tomado en igualdad de edades y proporción de sexos. Entre los estudiantes de Submarinismo 14 de los 50 han sabido responder bien a la pregunta y, entre los entrenadores, sólo 5 de 50 lo han hecho correctamente. A partir de este estudio y de esta muestra, ¿se puede decir que hay diferencias, estadísticamente significativas, entre estas personas con diferente oficio/estudios en cuanto al efecto causado por la pesca de arrastre a las poblaciones de Horsea?

2. Se ha aplicado un tratamiento de Bayas Atania para relajar a unos Tentacruel salvajes machos y hembras adormilados en medio de la ruta 118 en Hoenn. En las Tentacruel hembras 5 de 20 respondían favorablemente al tratamiento, en los Tentacruel macho 3 de 20 eran los que respondían favorablemente. ¿Se puede decir que hay diferencias significativas entre sexos en cuanto a la respuesta a este tratamiento?

3. Un centro de investigación de energías naturales que pretende usar la electricidad de Chinchou bien cuidados en las mismas condiciones, decide hacer el siguiente estudio piloto. A un grupo de 100 Chinchou se les ha examinado mediante dos test de electricidad de distintos ataques eléctricos. En primer lugar, a 50 de ellos se les ha pedido que usen impactruenos en una diana con un voltímetro y a otros 50 que usen chispa en otras dianas con voltímetros. Una vez hecho el primer test, se les daban 4 horas de descanso a todos y, luego, cada Chinchou hacia el otro modelo de test. Cada test se evaluaba con un rango de 100 a 1000 voltios, pero, en realidad se quería ver si llegaban o no a los 500 voltios (>500 voltios= apto) con cada ataque porque lo que se quería ver era si el porcentaje de aptos sería el mismo o no usando diferentes ataques. Los resultados obtenidos fueron los siguientes: El ataque impactrueno el 60% fue apto y el ataque chispa el 48% lo fue, con este desglose por subgrupos de valores de la variable:

4. Se quiere comparar las velocidades que pueden alcanzar los Finneon y su evolución Lumineon. Para ello se han usado 9 Finneon de entrenadores y 9 Lumineon de otros entrenadores, todos ellos voluntarios. Mediante una serie de pruebas de natación se evalúan las velocidades de cada uno de estos Pokemon. Las velocidades se miden en metros/segundos y los valores obtenidos son los siguientes:

 

¿Podemos decir que hay diferencias estadísticamente significativas en cuanto a las velocidades de ambas evoluciones de Pokemon?

5. Estamos comparando la cantidad de Slowpoke atacados por la caza furtiva con el fin de comercializar sus colas como alimento que hubo en las regiones de Hoenn y Kalos. En Hoenn hubo 8 acontecimientos y en Kalos 7. Una vez completado los recuentos obtuvimos la siguiente tabla:

¿Podemos afirmar que las diferencias son estadísticamente significativas?

6.Hemos tomado 14 Spheals de entrenadores y entrenadoras al azar del club náutico de Alola (8 machos y 6 hembras) y hemos visto cuantas volteretas pueden dar seguidas. Los resultados obtenidos son los siguientes:

¿Podemos afirmar que las diferencias son estadísticamente significativas?

7. Se ha realizado un estudio sobre la producción de toxinas creadas por Mareanie en diversos puntos de las costas de la ruta 13 en Teselia, y al cabo de 4 años se ha repetido el mismo estudio en las mismas zonas. Se trataba de ver si la producción de toxinas había disminuido o serían estables. Los resultados fueron los siguientes:

¿Podemos afirmar que hay diferencias estadísticamente significativas entre los dos tiempos?

8. Estamos analizando el número de “blooms” bioluminiscentes causados por dinoflagelados que ha habido del día 1 al 9 de mayo, realizando una cuenta diferente cada día, y el número de “blooms” que ha habido los mismos días, pero en el mes de septiembre:

¿Podemos afirmar que hay diferencias significativas entre los dos meses?