1.En la muestra (1, 1, 2, 2, 2, 5, 5, 7, 7):

a.La mediana es 3,5.

b.3.5 es el percentil 40.33.

c. El rango intercuartílico es 6.

d.El percentil 22,22 es 1,5.

2.En dos estudios distintos tenemos las siguientes correlaciones r=-0.5 (p=0.0001) y r=0.5 (p=0.09), respectivamente. Podemos decir:

a.Con la misma magnitud de correlación no es posible que se obtengan estos p-valores distintos.

b.La diferencia de p-valor entre ambos estudios es debido al signo distinto.

c.El tamaño muestral del primer estudio será mayor que el del segundo estudio.

d.En el primer estudio tenemos suficiente capacidad predictiva, en cambio en el segundo no.

3.Estamos interesados en saber en cuántos puntos de una playa se supera un cierto nivel de un contaminante. Para ello se toman al azar 400 muestras a lo largo del río. En 20 de ellas se supera ese nivel. Un intervalo de confianza del 99.5% del porcentaje de puntos del río donde se supera dicho nivel es:

a.(2.82, 7.18).

b.(1.73, 8.27).

c.(3.91, 6.09).

d.(0.64, 9.36).

4.¿Cuál de las siguientes afirmaciones es cierta?

a.La ji-cuadrado evalúa si hay relación entre dos variables cuantitativas.

b.El coeficiente de determinación superior al 50% indica buena capacidad predictiva, aunque el p-valor de la correlación sea superior a 0.05.

c.La significación de una V de Crámer la podemos evaluar por el p-valor de la ji-cuadrado.

d.Si la tabla de contingencias observada y la tabla de contingencias esperada son iguales el p-valor será 0.

5.En cuál de las siguientes regresiones lineales simples podremos hacer mejores predicciones:

a)y=0.02x+1; IC del 95% de la correlación (0.1, 0.2).

b)y=4000x+1; IC del 95% de la correlación (0.05, 0.3)

c)y=0.7x-34; IC del 95% de la correlación (0.3, 0.8)

d)y=3x+20; IC del 95% de la correlación (-0.1, 0.4).

6.Estamos tratando de asociar la presencia o la ausencia de una especie fitoplanctónica con la presencia o ausencia de una especie zooplanctónica en muestras marinas de distintas zonas del mediterráneo. Hemos codificado la ausencia con un 0 y la presencia con un 1. Hemos calculado la correlación de Pearson y nos da r=0.8 (p=0.001), podemos decir:

a.Que hay una relación significativa entre esas dos variables.

b.Que la relación no tiene suficiente capacidad predictiva porque tiene una R2 menor del 50%.

c.Que la significación dependerá del tamaño de muestra que tengamos.

d.Ninguna de las respuestas anteriores es correcta.

7.¿Cuál de las siguientes afirmaciones es cierta?:

a.La comprobación de la normalidad la hacemos con el test de la t de Student.

b.Si se aplica una t de Student de muestras independientes y varianzas desiguales en una de las dos muestras o en las dos no hay suficientes ajuste a la distribución normal.

c.Si dos intervalos de la media no se solapan en dos muestras independientes podemos afirmar que el p-valor en un contraste de hipótesis de igualdad de medias es inferior a 0.05.

d.Ninguna de las tres afirmaciones anteriores es cierta.

8.¿Cuál de las siguientes afirmaciones es cierta?:

a.En una regresión si la R2 es superior al 50% tenemos una relación estadísticamente significativa entre las variables de la regresión.

b. La R2 es menor del 50% no existe relación estadísticamente significativa entre las variables.

c.Una correlación estadísticamente significativa genera una R2 superior al 50%.

d.Ninguna de las afirmaciones anteriores es cierta.

9.Estamos relacionando en tres zonas distintas la presencia de cuatro especies distintas del zooplancton. Hemos aplicado una ji-cuadrado y el valor es 4.02. Entonces:

a.No podemos decir que hay relación porque 4.02 es menor que 21.02.

b.No podemos decir que hay relación porque 4.02 es menor que 12.59.

c.No podemos decir que hay relación estadísticamente significativa porque 4.02 es mayor que 3.84.

d.Podemos decir que hay relación estadísticamente significativa porque 4.02 es mayor que 3.84.

10.Un intervalo de confianza del 99.5% descriptivo de la variable en una muestra con media muestral 20, desviación estándar 1 y tamaño muestral de 100 es:

a.(17, 23).

b.(19.7, 20.5).

c.(19.97, 20.03).

d.(19, 21).

11.¿Cuál de las siguientes afirmaciones es cierta?

a.Si en una comparación la potencia estadística superior al 80% habrá diferencias estadísticamente significativas.

b.En el test de la t de Student de muestras relacionadas se comparan medianas.

c.En una técnica de comparación de muestras independientes con un intervalo de confianza del 95% de la resta de las medias de (-0.9, 1.12) podemos decir que el test de comparación de medias tendría un p-valor inferior a 0.05.

d.En un ANOVA de un factor con tres niveles si los intervalos de confianza de las medias son (1.2, 2.7), (1.9, 3.1) y (2.3, 3.8) el p-valor nos dará superior a 0.05.

12.En un estudio donde se quiere comparar la cantidad de un contaminante en las playas de dos poblaciones distintas tenemos 50 observaciones en cada una de las dos playas. El test de Shapiro-Wilk de ambas muestras nos proporciona un p-valor mayor que 0.05. El test de Fisher-Snedecor nos proporciona una p=0.001. Es cierto lo siguiente:

a.Debemos aplicar el test de la t de Student para varianzas desiguales.

b.Debemos aplicar el test de la t de Student para varianzas iguales.

c.Debemos aplicar el test exacto de Fisher.

d.Debemos aplicar el test de Mann-Whitney.

13.En un estudio de comparación de dos poblaciones partimos de unos datos iniciales concretos y calculamos el p-valor con la técnica adecuada. Seguidamente disminuimos el tamaño de muestra de ambas poblaciones obteniendo la misma media y desviación estándar en ambas muestras y volvemos a calcular el p-valor. Después detectamos que la desviación estándar era más baja de la que habíamos calculado y volvemos a calcular el p-valor. Finalmente, detectamos que la diferencia de medias es más grande de la que habíamos calculado previamente y volvemos a calcular el p-valor. ¿Cuál de las siguientes es la secuencia de p-valores que podríamos tener?

a.0.54/0.23/0.25/0.12.

b.0.66/0.86/0.44/0.22.

c.0.23/0.25/0.34/0.23.

d.0.23/0.31/0.19/0.31.

14.Se analiza el porcentaje de una especie en el fitoplancton en 20 puntos del océano pacífico y 20 puntos del océano atlántico. ¿En cuál de los casos podemos decir que hay diferencias estadísticamente significativas?

a.Pacífico: IC 95%: (23.4, 26.5); Atlántico: IC 95%: (22.4, 27.4).

b.Pacífico: IC 95%: (10.4, 12.9); Atlántico: IC 95%: (12.5, 17.2).

c.Pacífico: IC 95%: (33.5, 36.5); Atlántico: IC 95%: (37.2, 39.9).

d.Pacífico: IC 95%: (21.1, 21.5); Atlántico: IC 95%: (21.3, 21.8)

15.Hemos analizado la cantidad de biomasa en una zona en dos tiempos distintos (T1 y T2). El análisis lo han realizado tres operadores, tres analistas distintos que se quieren comparar. Cada muestra cada operario la analiza por duplicado. Los resultados son los siguientes:

¿Cuál es la afirmación más razonable?:

a.Factor T: p>0.05. Factor Op: p>0.05. Interacción: p>0.05.

b.Factor T: p>0.05. Factor Op: p>0.05. Interacción: p<0.05.

c.Factor T: p<0.05. Factor Op: p<0.05. Interacción: p<0.05.

d.Factor T: p>0.05. Factor Op: p<0.05. Interacción: p>0.05.

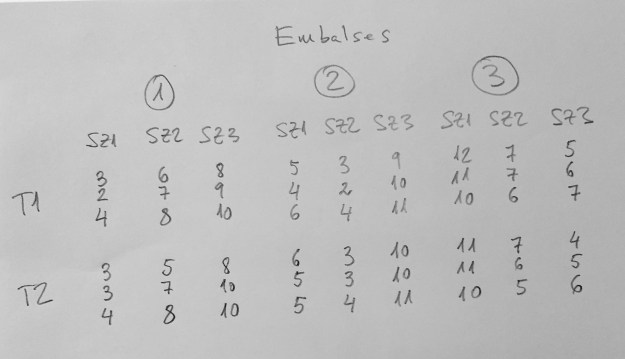
16.Supongamos que hemos tomado tres embalses españoles al azar con la voluntad de conocer la variabilidad que hay en ellos de un determinado contaminante. Tomamos tres subzonas también al azar, en cada embalse, para conocer la variabilidad interna dentro de los embalses. Queremos también conocer si las diferentes técnicas definidas para evaluar este contaminante presentan variación (hay unas quince que se han definido en la bibliografía). Para ello elegimos dos de ellas al azar y las evaluamos por triplicado en cada muestra que tenemos. Los resultados son los siguientes:

¿Qué modelo tenemos?

a.Embalse, Subzona y Técnica factores aleatorios. Subzona anidado en Zona y Técnica cruzado con las otras dos.

b.Embalse, Subzona y Técnica factores fijos. Zona y Subzona cruzados. Técnica anidado tanto en Zona como en Subzona.

c.Embalse fijo, Subzona aleatorio y Técnica fijo. Subzona anidado en Zona y Técnica cruzado cruzado con las otras dos.

d.Embalse aleatorio, Subzona fijo y Técnica aleatorio. Subzona anidado en Zona y Técnica anidado en Subzona.

17.¿Qué error podríamos estar cometiendo si al comparar dos tratamientos tenemos una potencia del 50% y el p-valor que obtenemos es de 0.02?

a.No podemos cometer error porque la potencia estadística es superior al 80%.

b.El error de tipo I.

c.El error de tipo II.

d.Ambos errores: El error de tipo I y el error de tipo II.

18.¿Cuál de las siguientes afirmaciones es cierta?

a.Una potencia del 80% se corresponde con un error de tipo I de 0.20.

b.Si en dos muestras independientes, que se ajustan a la normalidad, no hay igualdad de varianzas se aplica el Test de Mann-Whitney.

c.En una correlación de Pearson con una correlación estadísticamente significativa no podemos garantizar que habrá suficiente capacidad predictiva.

d.En una comparación de medias, con un intervalo de confianza del 95% de la diferencia de medias como el siguiente: (-1.13, 0.98), podemos decir que hay diferencia de medias estadísticamente significativa.

19.¿Cuál de las siguientes afirmaciones es cierta?:

a. En un ANOVA de dos factores cruzados la interacción será significativa si alguno de los dos factores lo es.

b. Un intervalo de confianza del 95% de la correlación de (-0.05, 0.05) va asociado a un p-valor de 0.05.

c. Una R2 de 50% va asociado a una correlación de 0.5.

d. Con una ji-cuadrado con un valor de 3.12 podemos decir que no tenemos una relación estadísticamente significativa, independientemente del números de filas y columnas de la tabla de contingencias.

20.Se quiere hacer un pronóstico del porcentaje de peces de una especie determinada que hay en una zona. Tenemos la sospecha,  por estudios similares, que nos vamos a encontrar un valor bastante próximo al 25%. ¿Qué tamaño muestral de peces necesitamos tomar para tener un intervalo del 99,5% con un radio de 5%?:

a.200.

b.300.

c.675.

d.475.

 

1d: Basta dividir los 2 valores que quedan por debajo de 1.5 por los 9 de la muestra para tener un 22.22%.

2c: Para una correlación de la misma magnitud, si el p-valor cambia será debido al tamaño muestral. Cuanto mayor tamaño tengamos menor será el p-valor.

3b: Si se calcula el intervalo de confianza de una variable dicotómica según el tema 3, teniendo en cuenta de que como el intervalo es del 99.5% debemos usar un 3 en lugar de un dos en la fórmula, obtenemos este resultado.

4c: La V de Crámer no tiene un p-valor asociado, pero sí lo tendremos de la ji-cuadrado previa que haremos. El p-valor de ésta nos marca también la significación del valor de relación que nos dé la V de Crámer.

5c: Porque la correlación tiene mayor magnitud.

6d: Estamos hablando de variables cualitativas, ninguna de las técnicas cuantitativas nos son útiles aquí.

7c: Hacer intervalos de confianza de las dos medias a comparar y ver si se solapan o no es equivalente a hacer un contraste de hipótesis. Si estos intervalos no se solapan habrá diferencia significativa.

8d: Significación y capacidad predictiva son dos conceptos independientes entre ellos.

9b: El umbral en una tabla 3×4 es 12.59. Como el valor de la ji-cuadrado es menor no podemos decir que hay relación.

10a: Como es descriptivo sólo importa la desviación estándar, no el tamaño de muestra. Como es del 99.5% cogemos tres desviaciones estándar.

11d: Los tres intervalos se solapan, por lo tanto no habrá diferencias significativas entre los tres grupos.

12a: Hay normalidad pero no hay igualdad de varianzas.

13b: Disminuir tamaño de muestra, disminuir la desviación estándar y, finalmente, aumentar la diferencia de medias, va asociado de subida, bajada y de nuevo bajada del p-valor.

14c: Es el única caso donde los intervalos de confianza no se solapan.

15b: En ninguno de los dos factores podemos ver una diferencia clara de medias. Sin embargo, la interacción es evidente. No se comporta de forma paralela cada operador respecto a cada una de las dos técnicas.

16a: Claramente los tres factores son aleatorios. Subzona anidado en Embalse. Y técnica cruzado con los otros dos factores.

17b: Como el p-valor es menor que 0.05 rechazaríamos la Hipótesis nula por lo que podríamos estar cometiendo el error de tipo I.

18c: Significación y capacidad predictiva son dos conceptos independientes entre ellos.

19d: Como el valor es inferior a 3.84 que es el umbral más pequeño posible, podemos afirmar lo que dice el punto d.

20c: Debemos aplicar la fórmula para la determinación del tamaño de muestra del Tema 16 para variables dicotómicas teniendo en cuenta que tenemos la información del 25% y que el intervalo que queremos es del 99.5% (por lo que tendremos que cambiar el 4 por un 9 en la fórmula)

 

Se trata de un ANOVA de tres factores cruzados con dos factores fijos y uno aleatorio. Si observamos los cocientes en el archivo del Herbario de técnicas dedicado a tres factores veremos que la solución está en el cuatro listado. La solución es la siguiente:

El modelo concreto utilizado es el siguiente:

Pero, cuidado, en nuestro caso el factor aleatorio es el tercero, no el primero. Lo importante no son las letras sino cuáles son signos de un factor fijo y cuáles de un factor aleatorio.

 

 

La siguiente base de datos de pacientes de demencia tiene la siguientes variables:

P=Número de Paciente

G=Grupo (Control, Alzhéimer, Demencia vascular y Demencia mixta)

S=Sexo (1=hombre, 2=mujer)

E=Edad

ES=Nivel de estudios (0=Analfabeto, 1=Primarios, 2=Mediosy 3=Superiores)

D=Diabetes mellitus

H=Hipertensión

C=Enfermedad coronaria

En estas variables 0 significa no y 1 sí.

MM0=Valor del Mini-Mental State Examination (MMSE) en el diagnóstico

MM3=Valor del Mini-Mental a los 3 años del diagnóstico

VH3=Volumen del Hipocampo a los 3 años del diagnóstico en cc

P	G	S	E	ES	D	H	C	MM0	MM3	VH3
1	Control	1	60	1	1	1	0	27	27	5.5
2	Control	1	79	2	0	0	0	27	27	5.5
3	Control	1	71	2	0	1	0	27	28	5.7
4	Control	1	66	1	1	0	1	28	27	5.4
5	Control	2	69	0	0	0	1	27	27	5.3
6	Control	2	62	2	0	1	0	30	30	6.1
7	Control	2	60	1	1	1	0	28	28	6.0
8	Control	2	63	1	1	0	0	27	27	5.4
9	Control	2	77	1	0	0	1	28	28	5.6
10	Control	1	63	2	0	1	0	28	28	5.6
11	Control	1	79	1	1	1	0	29	29	5.8
12	Control	1	55	3	1	1	0	27	27	5.5
13	Control	2	72	1	0	0	0	29	29	5.5
14	Control	2	68	1	0	0	0	29	29	5.7
15	Control	1	81	2	0	1	1	28	28	5.6
16	Control	1	71	1	0	1	1	27	27	5.3
17	Control	2	61	2	0	0	0	27	27	5.4
18	Control	2	76	1	1	0	0	27	27	5.4
19	Control	2	72	1	0	0	0	30	29	6.2
20	Control	2	63	0	0	1	0	28	28	5.7
21	Control	2	67	2	0	0	0	28	28	5.5
22	Control	1	69	1	1	1	0	28	28	5.6
23	Control	1	60	1	0	0	0	28	28	5.7
24	Control	2	64	1	0	0	1	28	28	5.9
25	Control	2	73	2	1	1	1	30	30	6.0
26	Control	2	66	1	1	1	0	29	29	5.5
27	Control	2	76	3	0	0	0	27	28	5.8
28	Control	1	75	1	0	0	0	27	27	5.6
29	Control	2	62	1	1	1	1	29	29	5.6
30	Control	2	78	2	1	1	0	28	27	5.6
31	Control	1	57	1	0	0	0	29	27	5.2
32	Control	1	58	2	0	0	0	28	29	5.7
33	Control	2	63	1	1	1	0	28	29	5.8
34	Control	2	65	1	0	0	0	26	27	5.5
35	Control	2	74	0	0	0	1	27	27	5.2
36	Control	2	61	2	1	1	1	29	29	6.2
37	Control	1	71	1	0	0	0	27	29	6.2
38	Control	2	71	1	0	0	0	27	28	5.5
39	Control	2	63	1	1	1	0	28	28	5.4
40	Control	1	67	2	1	0	0	29	29	6.0
41	Control	1	69	1	0	1	0	28	30	6.1
42	Control	2	63	1	0	1	1	27	29	5.6
43	Control	2	75	1	1	0	1	29	27	5.8
44	Control	2	69	1	1	0	0	27	26	5.1
45	Control	2	62	2	0	1	0	30	30	5.6
46	Control	2	66	2	0	0	0	27	28	5.8
47	Control	1	57	1	1	0	1	26	26	4.9
48	Control	1	62	1	0	1	0	29	28	5.9
49	Control	1	59	0	0	1	0	29	28	5.4
50	Control	2	72	2	1	0	0	28	28	5.4
51	Alzhéimer	2	78	1	0	0	1	24	22	4.4
52	Alzhéimer	2	73	1	0	1	0	24	21	4.3
53	Alzhéimer	2	63	1	0	0	0	23	21	4.2
54	Alzhéimer	1	65	2	1	0	0	23	20	4.0
55	Alzhéimer	2	67	1	1	1	0	23	20	4.1
56	Alzhéimer	2	66	0	0	1	0	24	20	4.0
57	Alzhéimer	1	75	1	0	0	1	22	18	3.6
58	Alzhéimer	1	62	1	1	0	1	21	17	3.4
59	Alzhéimer	2	71	2	0	1	0	23	20	4.1
60	Alzhéimer	2	59	1	0	0	0	20	16	3.3
61	Alzhéimer	2	66	2	1	0	0	24	21	4.3
62	Alzhéimer	2	64	1	1	1	0	23	20	4.1
63	Alzhéimer	2	65	1	0	1	0	22	17	3.5
64	Alzhéimer	1	71	0	0	0	1	24	22	4.5
65	Alzhéimer	1	68	2	1	0	1	21	18	3.7
66	Alzhéimer	1	73	1	0	1	0	21	20	4.1
67	Alzhéimer	2	64	1	0	1	0	21	18	3.6
68	Alzhéimer	2	60	1	1	0	0	22	19	3.8
69	Alzhéimer	2	76	2	1	0	1	21	18	3.6
70	Alzhéimer	2	64	1	0	1	0	23	20	4.0
71	Alzhéimer	1	68	3	0	0	0	22	18	3.7
72	Alzhéimer	2	63	1	1	0	0	23	20	4.1
73	Alzhéimer	2	68	1	0	1	1	21	18	3.7
74	Alzhéimer	1	73	2	0	0	0	21	20	4.1
75	Alzhéimer	1	62	1	1	0	0	20	17	3.4
76	Alzhéimer	2	65	2	1	1	0	23	19	3.9
77	Alzhéimer	2	76	1	0	1	0	22	20	4.0
78	Alzhéimer	2	61	1	0	0	0	21	17	3.4
79	Alzhéimer	2	67	0	1	0	1	21	18	3.7
80	Alzhéimer	2	64	2	0	1	1	21	18	3.7
81	Alzhéimer	1	64	1	0	1	0	24	21	4.3
82	Alzhéimer	2	69	1	1	0	0	20	18	3.7
83	Alzhéimer	2	74	1	1	0	0	22	19	3.9
84	Alzhéimer	2	57	2	0	1	0	24	19	3.9
85	Alzhéimer	1	67	1	0	0	0	23	20	4.0
86	Alzhéimer	1	73	3	1	0	1	22	19	3.9
87	Alzhéimer	2	74	1	0	1	1	21	19	3.8
88	Alzhéimer	2	72	1	0	1	0	21	18	3.7
89	Alzhéimer	2	78	2	0	0	1	24	21	4.3
90	Alzhéimer	2	68	2	0	0	0	23	19	3.8
91	Alzhéimer	1	73	1	0	1	0	20	18	3.7
92	Alzhéimer	2	64	1	0	0	0	23	20	4.0
93	Alzhéimer	1	75	0	1	0	0	22	18	3.7
94	Alzhéimer	1	63	2	0	1	0	23	20	4.0
95	Alzhéimer	2	79	1	0	1	1	21	20	4.0
96	Alzhéimer	2	77	1	1	0	1	24	22	4.4
97	Alzhéimer	2	76	1	1	0	0	21	18	3.7
98	Alzhéimer	2	62	2	0	0	0	22	17	3.4
99	Alzhéimer	1	70	1	0	0	0	21	18	3.7
100	Alzhéimer	2	73	1	1	1	0	21	19	3.9
101	Vascular	2	73	1	1	1	0	20	17	5.3
102	Vascular	1	75	1	0	0	1	20	14	5.5
103	Vascular	1	72	2	0	1	1	20	14	5.5
104	Vascular	2	71	1	1	0	0	21	13	5.7
105	Vascular	2	78	2	0	0	0	18	12	5.4
106	Vascular	2	61	1	0	1	0	20	14	5.3
107	Vascular	1	66	1	1	0	1	21	16	6.1
108	Vascular	1	69	0	0	0	0	19	13	6.0
109	Vascular	2	76	2	0	1	0	20	14	5.4
110	Vascular	2	77	1	0	1	0	18	16	5.6
111	Vascular	2	73	1	1	0	0	20	14	5.5
112	Vascular	2	61	1	1	0	0	20	13	5.5
113	Vascular	1	72	2	0	1	1	18	12	5.7
114	Vascular	2	56	1	0	0	1	20	18	5.4
115	Vascular	2	63	1	1	0	0	20	14	5.3
116	Vascular	1	67	1	1	1	0	20	16	6.1
117	Vascular	1	63	3	1	1	0	21	14	6.0
118	Vascular	2	73	2	1	0	0	20	14	5.4
119	Vascular	2	55	1	1	0	0	19	12	5.6
120	Vascular	2	65	2	0	0	1	20	13	5.5
121	Vascular	2	58	1	1	0	1	21	16	5.5
122	Vascular	1	74	1	1	1	0	21	15	5.7
123	Vascular	1	61	1	0	1	0	20	15	5.4
124	Vascular	2	70	2	1	1	1	21	14	5.3
125	Vascular	2	58	1	1	1	0	20	14	6.1
126	Vascular	2	62	1	1	1	0	21	14	6.0
127	Vascular	2	63	1	0	1	0	21	14	5.4
128	Vascular	1	61	2	0	0	0	18	13	5.6
129	Vascular	2	71	1	1	1	0	18	11	5.6
130	Vascular	2	60	1	1	1	1	21	15	5.8
131	Vascular	1	77	1	0	1	1	20	12	5.5
132	Vascular	1	73	1	0	1	0	19	13	5.2
133	Vascular	2	69	2	1	0	0	18	13	5.7
134	Vascular	2	69	1	0	0	0	18	12	5.8
135	Vascular	2	78	2	0	1	0	18	10	5.5
136	Vascular	1	57	1	1	0	0	21	15	5.2
137	Vascular	1	64	3	1	0	1	19	14	6.2
138	Vascular	2	60	1	1	1	1	20	14	6.2
139	Vascular	2	62	1	1	1	0	18	13	5.5
140	Vascular	2	72	2	1	0	0	18	12	5.4
141	Vascular	2	72	1	0	0	0	19	12	6.0
142	Vascular	1	79	2	1	0	1	19	13	6.1
143	Vascular	2	62	1	1	1	0	18	12	5.6
144	Vascular	2	75	1	1	1	1	21	14	5.8
145	Vascular	1	68	1	1	0	0	21	15	5.1
146	Vascular	1	60	2	0	0	0	19	12	5.6
147	Vascular	2	60	1	1	1	0	19	12	5.8
148	Vascular	2	79	1	1	1	0	20	15	4.9
149	Vascular	1	67	1	0	0	0	18	14	5.9
150	Vascular	1	59	3	0	0	1	18	12	5.4
151	Mixta	2	65	1	1	1	1	21	15	4.2
152	Mixta	2	78	1	0	0	0	20	16	4.1
153	Mixta	2	66	1	0	0	0	20	16	4.2
154	Mixta	2	64	1	1	1	0	19	15	4.1
155	Mixta	1	55	2	1	1	0	21	17	4.3
156	Mixta	2	63	1	0	0	0	21	17	4.5
157	Mixta	2	66	2	0	0	1	20	16	4.2
158	Mixta	1	65	1	1	1	1	19	15	4.2
159	Mixta	1	70	1	0	1	0	21	17	4.2
160	Mixta	2	71	1	0	1	0	19	15	4.2
161	Mixta	2	64	2	1	0	0	21	18	4.3
162	Mixta	1	79	1	1	0	0	20	16	3.8
163	Mixta	1	63	1	0	1	1	18	15	4.0
164	Mixta	2	60	1	0	0	0	20	16	4.3
165	Mixta	2	56	1	1	0	0	19	16	4.4
166	Mixta	2	78	2	1	1	0	19	13	3.5
167	Mixta	2	67	1	0	1	0	19	15	4.1
168	Mixta	1	74	3	0	0	0	19	17	4.2
169	Mixta	2	60	1	1	0	1	21	14	4.1
170	Mixta	2	77	1	0	1	1	18	14	3.7
171	Mixta	1	72	2	0	1	0	21	18	4.6
172	Mixta	1	76	1	1	0	0	20	15	4.1
173	Mixta	2	71	2	0	0	0	18	14	3.9
174	Mixta	2	64	1	0	1	0	21	16	4.1
175	Mixta	1	79	1	1	0	0	20	15	3.9
176	Mixta	1	58	2	1	0	0	20	16	3.8
177	Mixta	2	73	2	1	1	1	20	16	4.3
178	Mixta	2	72	1	0	0	0	18	13	3.5
179	Mixta	2	70	1	0	0	0	20	14	3.7
180	Mixta	2	72	1	1	1	0	19	15	4.2
181	Mixta	1	70	2	0	0	0	21	19	4.8
182	Mixta	2	74	1	0	1	0	20	16	3.9
183	Mixta	2	78	1	1	0	1	19	15	4.1
184	Mixta	1	60	1	1	0	1	20	15	4.1
185	Mixta	1	64	1	0	1	0	20	16	4.2
186	Mixta	2	62	2	0	0	0	20	16	3.9
187	Mixta	2	67	1	1	0	0	21	17	4.3
188	Mixta	2	79	2	0	1	0	21	16	4.2
189	Mixta	1	70	1	0	1	0	18	14	3.9
190	Mixta	1	70	1	1	0	1	19	14	3.4
191	Mixta	2	77	0	1	0	1	18	14	3.6
192	Mixta	2	78	2	0	1	0	19	14	3.8
193	Mixta	2	66	1	0	0	0	20	14	3.6
194	Mixta	2	74	1	1	1	0	21	15	4.0
195	Mixta	1	78	1	1	1	1	20	16	3.8
196	Mixta	2	67	2	0	1	0	21	16	4.4
197	Mixta	2	72	1	0	1	0	19	15	4.1
198	Mixta	1	70	3	1	1	0	18	13	3.4
199	Mixta	1	68	1	0	1	0	20	17	4.5
200	Mixta	2	75	1	0	1	0	19	14	3.6

Ver la capacidad discriminativa para diferenciar entre tener o no demencia y cuál de las tres demencias se tiene, en el momento del diagnóstico; o sea, con todas las variables excepto las dos últimas y ver, luego, la capacidad discriminativa que se tiene a los tres años del diagnóstico, ahora sí con las todas las variables.

1.

2.

3.

4.

5.

 

 

1.Tenemos que estudiar la calidad del producto de los operarios de una empresa. Cogemos tres operarios al azar para el estudio. Queremos ver, también, la influencia de las máquinas con las que se trabaja. Se eligen tres de las veinticinco que hay en la empresa. Cada trabajador opera con cada máquina para elaborar dos productos. Se estudia la calidad del 0 al 10 del producto final. La tabla ANOVA es la siguiente. Completarla:

A=Factor operario

B=Factor máquina

2.Tenemos el mismo caso que el estudio anterior pero ahora la diferencia es que sólo se cogen dos operarios y dos máquinas y el producto final que elaboran se estudia por parte de ocho evaluadores distintos. Cada evaluador estudia las dos réplicas de una única combinación de operador y máquina. Cada combinación de operador y máquina la estudian dos evaluadores. La tabla ANOVA es la siguiente. Completarla:

A=Factor operario

B=Factor máquina

C=Factor evaluador

3.Tenemos la intención de estudiar el nivel de limpieza de todas las playas en poblaciones superiores a 5.000 habitantes en el litoral catalán. Se eligen dos playas al azar para hacer el estudio. Se eligen, al mismo tiempo, tres subzonas en cada una de las playas porque se quiere evaluar, también, la heterogeneidad interna. Cada muestra se evalúa mediante dos sistemas de medida que se pretende comparar. Se hacen dos réplicas. La tabla ANOVA es la siguiente. Completarla:

A=Factor playa

B=Factor sistema de medida

C=Factor subzona de la playa

4. En un proceso industrial queremos evaluar dos clases de levadura, dos tipos de azúcar y dos temperaturas. Para ello se realizan todas las combinaciones posibles de los tres factores. Se realizan dos réplicas por cada condición experimental. La tabla ANOVA es la siguiente. Completarla.

A=Factor levadura

B=Factor azúcar

C=Factor temperatura

5. En un proceso industrial queremos evaluar la variabilidad introducida por los operarios y, al mismo tiempo, queremos ver cómo influyen dos clases distintas de levadura y dos temperaturas diferentes. Para ello se realizan todas las combinaciones posibles de los tres factores. Se realizan dos réplicas por cada condición experimental. La tabla ANOVA es la siguiente. Completarla.

A=Factor operario

B=Factor levadura

C=Factor temperatura

Se ha hecho un estudio en dos zonas marinas que se quieren comparar. Se han hecho 20 observaciones en cada zona. Se ha analizado la temperatura, la salinidad, la abundancia relativa de la Especie A (especie del fitoplancton siempre presente) y la presencia o ausencia (1ó 0, respectivamente), en la muestra, de la Especie B y de la especie C.

Los resultados obtenidos son los siguientes:

ZONA	TEMP	SAL	EspA	EspB	EspC
1	12,4	35,6	1,31	1	0
1	13	35,8	1,30	0	1
1	12,3	34,7	1,25	0	1
1	12,8	34,7	1,30	0	1
1	12,9	35,9	1,37	0	1
1	13,1	34,6	1,37	0	0
1	13,2	35,7	1,40	0	0
1	13,1	34,7	1,38	1	0
1	12,8	34,7	1,32	1	0
1	12,9	35,9	1,31	1	0
1	13	34,6	1,30	1	1
1	12,3	34,7	1,30	0	1
1	12,8	34,7	1,34	0	1
1	12,9	35,9	1,38	0	1
1	13,1	34,6	1,36	0	0
1	13,2	35,9	1,33	1	0
1	14	34,6	1,42	1	0
1	13,1	34,7	1,35	0	0
1	12,8	34,7	1,34	0	0
1	12,9	35,9	1,38	0	1
1	13,1	34,7	1,38	1	0
1	12,8	34,7	1,32	1	0
1	12,9	35,9	1,31	1	0
1	13,1	34,6	1,36	0	0
1	13,2	35,9	1,33	1	0
1	14	34,6	1,42	1	0
1	13,1	34,7	1,35	0	0
1	12,8	34,7	1,34	0	0
1	12,9	35,9	1,38	0	1
1	13,1	34,7	1,38	1	0
1	12,8	34,7	1,32	1	0
1	12,9	35,9	1,31	1	0
1	13	34,6	1,30	1	1
1	12,3	34,7	1,30	0	1
1	12,8	34,7	1,34	0	1
1	12,8	34,7	1,30	0	1
1	12,9	35,9	1,37	0	1
1	13,1	34,6	1,37	0	0
1	13,2	35,7	1,40	0	0
1	13,1	34,7	1,38	1	0
2	14	35,8	1,50	0	1
2	14,3	34,7	1,46	1	1
2	14,4	34,7	1,49	0	1
2	13,9	35,9	1,43	1	0
2	13,8	34,6	1,38	0	1
2	14,6	35,7	1,49	1	0
2	14,4	34,7	1,45	1	0
2	13,9	35,8	1,44	1	0
2	13,8	34,7	1,43	1	0
2	13,9	34,7	1,44	1	0
2	13,8	35,9	1,45	1	1
2	14,6	34,6	1,53	0	1
2	13,9	35,7	1,40	0	1
2	13,8	34,7	1,44	1	1
2	13,9	34,7	1,41	0	1
2	13,8	35,9	1,39	0	0
2	14,6	34,6	1,50	1	0
2	14,4	34,7	1,52	0	1
2	13,9	34,7	1,44	1	0
2	14,6	35,9	1,50	1	0
2	14,4	34,7	1,49	0	1
2	13,9	35,9	1,43	1	0
2	13,8	34,6	1,38	0	1
2	14,6	35,7	1,49	1	0
2	14,4	34,7	1,45	1	0
2	13,9	35,8	1,44	1	0
2	14,4	34,7	1,49	0	1
2	13,9	35,9	1,43	1	0
2	14,4	34,7	1,49	0	1
2	13,9	35,9	1,43	1	0
2	13,8	34,6	1,38	0	1
2	14,6	35,7	1,49	1	0
2	14,4	34,7	1,45	1	0
2	13,9	35,8	1,44	1	0
2	14,4	34,7	1,49	0	1
2	14,6	34,6	1,53	0	1
2	13,9	35,7	1,40	0	1
2	14,4	34,7	1,52	0	1
2	13,9	34,7	1,44	1	0
2	14,6	35,9	1,50	1	0

1. Hacer una descriptiva de la variable TEMPERATURA.
2. Hacer una descriptiva de la variable Especie C.
3. Analizar si es posible, y con qué calidad, pronosticar la abundancia de la Especie A a partir de la temperatura.
4. Comprobar si hay relación entre la presencia o ausencia de las Especies B y C.
5. Comprobar si hay diferencias estadísticamente significativas en las dos zonas en cuanto a la variable TEMPERATURA.

El modelo y las esperanzas de los cuadrados medios es el siguiente:

Los cocientes de cuadrados medios para realizar los contrastes de hipótesis son los siguientes: