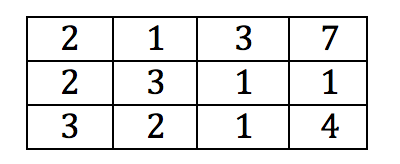
1) Hemos estudiado dos variables cualitativas mediante un test de la ji-cuadrado y posteriormente hemos calculado la V de Cramer resultando ser 0.9, ¿qué afirmación es cierta?

a) El p-valor de la ji-cuadrado es 0.9 también.

b) La tabla de contingencias con la que se ha trabajado podría ser una tabla 4×3.

c) La relación entre estas dos variables es positiva.

d) Necesitamos saber si el p-valor del test de la ji-cuadrado es mayor que 0.05 para poder darle valor a esta aparente fuerte asociación.

2) Si dos variables tienen una correlación de Pearson r=-0.8 (p<0.05), ¿cuál de los siguientes no es un modelo de regresión simple compatible con esta información?

a) y=-7x+12

b) y=-5x

c) y=-(3-x)

d) y=-(x-2)

3) ¿Cuál de las siguientes afirmaciones es cierta?

a) Una Odds ratio con un intervalo de confianza (0.23, 2.45) es significativa.

b) Una Odds ratio con un intervalo de confianza (2.33, 3.75) no es significativa.

c) Una Odds ratio con un p-valor de 0.67 es compatible con un intervalo de confianza como el siguiente: (1.23, 1.98).

d) Una Odds ratio con un p-valor de 0.34 es compatible con un intervalo de confianza como el siguiente: (0.93, 1.34).

4) ¿Cuál de las siguientes afirmaciones no es cierta?

a) Una correlación de Pearson con un intervalo de confianza (0.33, 0.88) no es significativa.

b) Una correlación de Pearson con un intervalo de confianza (-0.73, -0.25) es significativa.

c) Una correlación de Pearson con un p-valor de 0.37 es compatible con un intervalo de confianza como el siguiente: (-0.23, 0.98).

d) Una correlación de Pearson con un p-valor de 0.02 es compatible con un intervalo de confianza como el siguiente: (0.63, 0.78).

5) ¿Cuál de los siguientes modelos no es una Regresión lineal múltiple?:

a) y=2x-2y+7

b) y=3x+5z-3

c) y=7x-3z-1

d) y=6x-3x+1

6) En una Regresión logística simple es cierto:

a) La variable dependiente es cuantitativa y continua.

b) Debemos aplicar un Stepwise para seleccionar qué variables independientes son relevantes.

c) Una Odds ratio de 10 pasaría a ser de 0.1 si se cambiara la codificación de los ceros y los unos de la variable dependiente (si los ceros pasaran a ser unos y los unos pasaran a ser ceros) .

d) Una Odds ratio con un intervalo de confianza (0.45, 2.26) indica que se trata de una relación significativa por no contener el 0.

7) En una Regresión logística simple es cierto:

a) Un coeficiente que multiplica a la variable independiente con un intervalo de confianza (-0.6, 0.7) es compatible con un intervalo de confianza de la Odds ratio de (1.15, 2.33).

b) Un coeficiente que multiplica a la variable independiente con un intervalo de confianza (0.6, 0.9) es compatible con un intervalo de confianza de la Odds ratio de (1.8, 2.5).

c) Un coeficiente que multiplica a la variable independiente con un intervalo de confianza (-0.6, -0.4) es compatible con un intervalo de confianza de la Odds ratio de (1.45, 3.33).

d) Un coeficiente que multiplica a la variable independiente con un intervalo de confianza (0.8, 0.9) es compatible con un intervalo de confianza de la Odds ratio de (0.15, 1.33).

8) En una Regresión logística simple si tenemos un coeficiente que multiplica a la variable independiente con un intervalo de confianza como el siguiente (1.14, 1.66), podemos afirmar:

a) Que la Odds ratio no será significativa.

b) Que la Odds ratio será significativa y mayor que 1.

c) Que la Odds ratio será significativa y menor que 1.

d) Que la Odds ratio será 0.

9) En una V de Cramer no es cierto:

a) Es un valor entre el 0 y el 1.

b) Es una medida del grado de relación entre variables cualitativas.

c) Es un valor que será significativo si el Test de la ji-cuadrado de la tabla de contingencia es menor que 0.05.

d) Cuanto mayor es indica una menor relación entre las variables cualitativas.

10. En los datos siguientes:

y	x
1	7
1	9
1	5
1	6
1	8
0	2
0	3
0	4
0	2
0	6

Si hiciéramos una Regresión logística simple:

a) El coeficiente que multiplica a la variable independiente sería un valor mayor que 0.

b) El coeficiente que multiplica a la variable independiente será 0 porque tenemos un tamaño de muestra muy pequeño.

c) La Odds ratio será menor que 1.

d) La Odds ratio será mayor que 1 porque el coeficiente que multiplica a la variable independiente será menor que 0.

1c: Si tachamos el valor 20 quedan a su izquierda el 75% de valores y a su derecha el 25% de valores restantes.

2b: Si se aplica la fórmula para el cálculo del intervalo de confianza de una proporción visto en el tema 3 se obtiene este intervalo de confianza.

3d: El Error estándar será 0.1. Por lo tanto, sólo puede ser la respuesta d.

4b: Es el único caso donde pendiente y correlación siguen la misma suerte.

5d: 25 es el tercer cuartil, por lo tanto debajo de él tenemos el 75% aproximadamente de los enfermos.

6d. Puede ser posible tener una pendiente significativa y una R2 menor del 50% porque ambas cosas representan cosas diferentes.

7b: El primer cuartil es siempre, haya o no normalidad, un estimador del 25% de valores poblacionales inferiores.

8c: En una tabla 3×2 el valor de referencia es 5.99, por lo tanto, si el p-valor es menor de 0.05 es porque la ji-cuadrado ha dado un valor superior a 5.99.

9b: Es la única opción donde ser dicen cosas diferentes con el intervalo y con el p-valor.

10b: El valor de referencia es 12.59. Como 5.84 es menor el p-valor es mayor que 0.05 y por lo tanto no hay una relación estadísticamente significativa ente ambas variables.

1.El tercer cuartil de la muestra (8, 9, 10, 20, 22) es:

a) 21

b) 15

c) 20

d) No tiene tercer cuartil esta muestra

2. Si en un estudio sobre la prevalencia poblacional de una enfermedad tenemos una muestra de tamaño 10000 de los cuales 100 tienen esa enfermedad, un intervalo de confianza del 95% del porcentaje poblacional será

a) (0, 2)

b) (0.8, 1.2)

c) (1, 3)

d) (0.5, 1.5)

3. Tenemos una muestra de tamaño 10000 de una variable con media muestral igual a 100, desviación estándar igual a 10, que se ajusta bien a una distribución normal. ¿Cuál de las siguientes afirmaciones es cierta?

a) IC 95% de valores individuales: (90, 110)

b) IC 95% de la media: (99.7, 100.3)

c) IC 99.5% de valores individuales: (99, 101)

d) IC 68.5% de la media: (99.9, 100.1)

4. De las siguientes afirmaciones cuál es cierta:

a) En una Regresión es compatible un intervalo de confianza del 95% de la pendiente (-2.3, 0.7) con una de la correlación de (-0.6, -0.2)

En una Regresión es compatible un intervalo de confianza del 95% de la pendiente (2.8, 5.7) con una de la correlación de (0.4, 0.7)

En una Regresión es compatible una pendiente con un p-valor de 0.85 con una de la correlación  con una p-valor de 0.01

En una Regresión es compatible un intervalo de confianza del 95% de la pendiente (2.7, 5.7) con una de la correlación de (-0.6, -0.1)

5. Nos dicen que la concentración de dopamina en pacientes diagnosticados de Parkinson se puede resumir de la siguiente forma 5 (5- 25), podemos afirmar:

a) Que podemos representar a esa población de la siguiente forma: 5±5.

b) Entre 5 y 25 tenemos aproximadamente los mismos pacientes con Parkinson que con valores superiores a 25.

c) Por encima de 5 tenemos aproximadamente el 25% de la población de los pacientes de Parkinson.

d) Por debajo de 25 tenemos aproximadamente el 75% de los enfermos con Parkinson.

6. En una Regresión lineal simple es cierto:

a) Si la R2 es superior al 95% tenemos una relación estadísticamente significativa entre las variables de la regresión.

b) Un coeficiente de determinación del 25% es compatible con una correlación r=-2.5

c) Si la pendiente es mayor que 0 la correlación es significativa.

d) Una pendiente negativa y significativa puede tener un R2 menor del 50%.

7. ¿Cuál de las siguientes afirmaciones es cierta?

a) Un intervalo de confianza de la media del 95% es siempre más amplio que el intervalo de confianza del 95 de los valores individuales de la variable cuantitativa estudiada.

b) En una muestra con Asimetría estandarizada y una Curtosis estandarizada fuera de intervalo -2 y 2 por debajo del primer cuartil hay aproximadamente el 25% de la población.

c) Una correlación r=-0.75 (p>0.05) tendrá una pendiente de regresión negativa y significativa.

d) Si del primer cuartil a la mediana hay el doble de distancia que de la mediana al tercer cuartil también habrá el doble de observaciones aproximadamente en la población.

8. Si se realiza una ji-cuadrado para ver de analizar la relación entre dos variables cualitativas es cierto:

a) Si el valor del cálculo de la ji-cuadrado es menor que 3.84 la relación será significativa.

b) Si el p-valor es mayor que 0.05 el valor del cálculo de la ji-cuadrado es menor que 5.99.

c) Si el p-valor es menor que 0.05 el valor del cálculo de la ji-cuadrado es mayor que 5.99 si la tabla de contingencias es 3×2.

d) Si el valor del cálculo de la ji-cuadrado es mayor que 3.84 y la tabla de contingencias es 2×2 el p-valor es mayor que 0.05.

9. Si en una tabla de contingencias 3×2 en la que relacionamos dos variables cualitativas tenemos que el valor de la ji-cuadrado es 10.35 podemos afirmar:

a) Que estamos ante una relación significativa porque el valor 10.35 es superior al valor de referencia máximo aceptable para mantener la hipótesis nula en las tablas 3×2.

b) Que es imposible saber la significación porque no podemos saber si el p-valor es mayor o menor que 0.05.

c). No es una relación significativa porque el valor 10.35 nos proporcionará un p-valor superior a 0.05.

d) No sabemos si la relación es significativa pero sí sabemos que la correlación de Pearson será positiva y significativa.

9. ¿En cuál de las siguientes Odds ratio la información es incorrecta?

a) OR=0.3; IC 95% (0.1, 0.7); p=0.001

b) OR=0.5; IC 95% (0.1, 1.4); p=0.01

c) OR=3.1; IC 95% (0.56, 7.45); p=0.24

d) OR=0.5; IC 95% (0.2, 3.12); p=0.31

10.En la tabla

El valor de la ji-cuadrado de esta tabla de contingencias es 5.84

a) Como 5.84 es menor que 21.02 el p-valor será mayor que 0.05

b) No hay una relación estadísticamente significativa entre ambas variables cualitativas.

c) Como 5.84 es mayor que 3.84 el p-valor será mayor que 0.05

d) Esta tabla no tiene V de Crámer por no ser una tabla 2×2

1d: Se trata de dos correlaciones significativas y podremos hacer una Regresión lineal simple y, efectivamente, en el primer caso la pendiente será positiva y en la segunda negativa, porque el signo de la correlación y el de la pendiente coinciden.

2c: Observemos que las cuatro muestras sólo difieren en el último valor. La muestra con mayor desigualdad de reparto será la que el cuarto valor, que es el mayor de la muestra en todos los casos, sea el valor más grande. La muestra c es la que tiene el último valor mayor.

3a: El error estándar es 10/100 porque la raíz cuadrada de 10000 es 100. Por lo tanto, el error estándar es 0.1. Como el intervalo de confianza de la media que nos piden es del 99.5% necesitamos sumar y restar 3 veces el error estándar a la media. Esto nos da la muestra a.

4c: Tenemos una variable cuantitativa, muestras relacionadas y la variable resta no se ajusta a la distribución normal. Por lo que tenemos que aplicar o el Test de los signos o el Test de Wilcoxon.

5b: Los dos valores de Asimetría estandarizada y de Curtosis estandarizada están entre -2 y 2. Por lo tanto, la variable se ajusta bien a la distribución normal. Por lo tanto, si restamos dos veces y sumamos también dos veces a la media la desviación estándar obtendremos una estimación del intervalo del 95% de los valores individuales en la población.

6c: La correlación es negativa y significativa, por lo tanto, la Regresión lineal simple que hagamos tendrá una pendiente también con signo negativo y será también significativa. La suerte de la pendiente es la misma que la de la correlación.

7a: Cuanta menos dispersión tengamos en dos muestras a comparar menos cantidad de muestra necesitamos para encontrar diferencias significativas. Es lógico: si hay poca dispersión el valor que tengamos en un tamaño de muestra relativamente pequeño será más fiable que si hubiera habido mucha dispersión.

8b: El 10% de 50 son 5 y el 6% de 50 son 3. Por lo tanto, los valores absolutos de la muestras son 5 y 3. Por lo tanto, el valor esperado por grupo es de 4. Por lo tanto, aunque el tamaño de muestra por grupo es mayor de 30, el valor esperado por grupo es menor de 5. Debemos aplicar un Test exacto de Fisher.

9d: Variable cuantitativa, distribución normal de una y no de la otra. Por lo tanto, debemos aplicar el Test exacto de Fisher.

10a: El rango es 17 porque 7-(-10)=7+10=17.

1. De las correlaciones r=0.5 (p=0.03) y r=-0.4 (p=0.03) se puede afirmar lo siguiente:

a. Ninguna correlación es mayor que la otra porque el p-valor es el mismo.

b. Ninguna es significativa porque ninguna tiene un coeficiente de determinación superior al 50%.

c. La segunda es mayor que la primera.

d. Podemos hacer una Regresión lineal simple, en ambos casos. En la primera Regresión la pendiente será positiva y en la segunda la pendiente será negativa.

2. ¿Qué muestra de las siguientes tiene un índice de Gini mayor?

a. (1, 3, 3, 5, 12)

b. (1, 3, 3, 5, 11)

c. (1, 3, 3, 5, 13)

d. (1, 3, 3, 5, 10)

3. Si una muestra de tamaño 10000, que se ajusta bien a una distribución normal, tiene una media muestral de 40 y una desviación estándar de 10, un intervalo de confianza del 99,5% de la media poblacional será:

a. (39.7, 40.3)

b. (39, 41)

c. (39.9, 40.1)

d. (39.8, 40.2)

4. Se han estudiado los niveles de humedad relativa en una zona donde soplan dos tipos de viento bien distintos. Se tienen los valores de cada punto estudiado en un período donde soplaba un viento y en otro período en el que soplaba el otro tipo de viento. A la resta de los dos valores de humedad relativa de cada punto estudiado se ha aplicado un Test de Shapiro-Wilk dando un p-valor de 0.005. La técnica estadística a usar será:

a. Test de la t de Student de datos apareados.

b. Test de la t de Student de varianzas iguales.

c. Test de los signos.

d. Test de Mann-Withney.

5. En una muestra con una variable cuantitativa con Asimetría estandarizada igual a 1.43 y Curtosis estandarizada de -1.91, con media muestral igual a 120 y desviación estándar muestral igual a 10, podemos afirmar:

a. La mediana muestral será muy distinta de la media muestral.

b. Que el 95% de la población, aproximadamente, tiene valores entre 100 y 140.

c. Que no hay suficiente ajuste a la distribución normal.

d. Nos podemos fiar de la media muestral calculada pero no de la desviación estándar.

6. Si entre dos variables tenemos una correlación de Pearson: r=-0.76 (p<0.05), podemos afirmar lo siguiente:

a. No existe correlación significativa porque el p-valor es inferior a 0.05.

b. Existe correlación significativa porque las correlaciones negativas siempre son significativas.

c. Si hacemos una Regresión lineal simple la pendiente de la recta será también significativa y con signo negativo.

d. Si hacemos una Regresión lineal simple la pendiente de la recta será también significativa pero el signo puede ser positivo o negativo según otros criterios de los que ahora no disponemos.

7. ¿Qué afirmación, entre las siguientes, es cierta?:

a. Cuanta menos dispersión tenemos en dos grupos a comparar menos tamaño de muestra necesitaremos para encontrar diferencias significativas.

b. Cuanta más diferencia haya entre las medias muestrales de dos grupos a comparar más tamaño de muestra necesitaremos para detectar significación estadística.

c. En una técnica estadística de comparación de dos poblaciones aplicada a dos muestras con medias muestrales iguales, el p-valor será 0.

d. Si el p-valor en una comparación de dos poblaciones es menor de 0.05 entonces las dos medias poblacionales no son distintas significativamente.

8. Se ha estudiado si hay diferencias en el nivel de conocimientos de inglés sobresaliente entre estudiantes de escuelas públicas y de escuelas privadas en un país. Para comprobarlo se ha hecho un examen común de inglés a 50 estudiantes de un tipo de escuela y a 50 del otro tipo.  En la escuela privada el 10% tienen nivel de sobresaliente y en la pública el 6%. La técnica estadística a usar será:

a. Test de Mann-Whitney.

b. Test exacto de Fisher.

c. Test de proporciones.

d. Test de McNemar.

9. Se han estudiado las temperaturas en dos zonas distintas. Se ha aplicado un Test de Shapiro-Wilk en cada una de las dos muestras proporcionando los p-valores 0.2 y 0.01, respectivamente. La técnica estadística a usar será:

a. Test de la t de Student de varianzas iguales.

b. Test de Wilcoxon.

c. Test de la t de Student de varianzas diferentes.

d. Test de Mann-Withney

10. Sea la muestra (-10, -7, 0, 1, 3, 3, 3, 7). Podemos afirmar:

a. El rango es 17.

b. La mediana es 3.

c. El rango intercuartílico es 10.

d. El primer cuartil es -7.

1d: Como en toda técnica de comparación en la Hipótesis nula se afirma la igualdad, en este caso, como estamos con variables dicotómicas, afirma que las proporciones son iguales.

2b: Si las dos medias son iguales no tenemos ningún indicio para rechazar la Hipótesis nula de igualdad. Además el tamaño de muestra es muy pequeño. Observemos que de los cuatro p-valores dos son de rechazo de esa hipótesis, por ser menor que 0.05. Otro es de aceptación pero muy justa. El otro p-valor es de 1 que indica que no tenemos ninguna razón para rechazar esa hipótesis, que es lo que es cierto con esta información. Cuando comparamos dos muestras con la misma media siempre tendremos un p-valor de 1.

3d: Como el p-valor es menor de 0.05 rechazaremos la Hipótesis nula. En Estadística los criterios de decisión son siempre los mismos.

4d: Si en los test para comprobar la normalidad tenemos p-valores inferiores a 0.05 significa que no tenemos ajuste a la distribución normal, por lo tanto debemos aplicar directamente el Test de Mann-Withney sin aplicar el Test de Fisher-Snedecor.

5d: Si hubiera habido normalidad de las dos muestras entonces hubiera sido imprescindible aplicar el Test de Fisher-Snedecor.

6c: Al aumentar el tamaño de muestra las diferencias en las medias muestrales que tengamos son más consistentes, más seguras, más extrapolables a lo que puede suceder en las poblaciones.

7d: No hay normalidad en ninguna de las dos muestras, por lo tanto el Test de Fisher-Snedecor aplicado era innecesario. Debíamos ir directamente a aplicar un Test de Mann-Withney.

8a: Variables dicotómicas, muestras independientes y tamaño muestral, por muestra, menor que 30. Por lo tanto, hay que aplicar el Test exacto de Fisher.

9a: Variables continuas, muestras dependientes, normalidad de las restas. Debemos aplicar el Test de la t de Student de datos apareados.

10b: Variables dicotómicas, muestras independientes. El tamaño de muestra es mayor que 30 pero el valor esperado por grupo es de 3, porque los observados son 4 y 2 que hacen un promedio de 3. Como 3 es menor que 5 no se cumple la segunda condición para aplicar un Test de proporciones. Por lo tanto, debemos aplicar el Test exacto de Fisher.

 

1. En el Test de McNemar una de las siguientes afirmaciones es cierta:

a. El p-valor siempre es mayor de 0.05.

b. Es equivalente a un Test exacto de Fisher.

c. Se necesita una variable respuesta dicotómica y que las muestras sean independientes.

d. La Hipótesis nula afirma que las dos poblaciones comparadas son de proporciones iguales.

2. Si estamos haciendo una comparación de medias de dos poblaciones con dos muestrales de tamaño 3 cada una, con medias muestras iguales y con una desviación estándar de 5 y 6 respectivamente, ¿cuál es el p-valor más razonable para el contraste de hipótesis de igualdad de medias?

a. 0.001.

b. 1.

c. 0.000008.

d. 0.05.

3. Si estamos haciendo una comparación de proporciones de dos muestras independientes y el p-valor obtenido es 0.04, la decisión será la siguiente:

a. Aceptaremos la Hipótesis nula.

b. Rechazaremos la Hipótesis alternativa.

c. Volveremos a hacer el estudio debido a lo ajustado del p-valor.

d. Aceptaremos la Hipótesis alternativa.

4. Se está evaluando la satisfacción de la información meteorológica que da un medio de comunicación mediante una encuesta a sus oyentes que deben proporcionar una nota del 0 al 10. Se pretende comparar la satisfacción media que muestran las personas que viven en ambiente urbano y en ambiente rural. Se ha tomado una muestra en cada uno de los dos ámbitos y se ha aplicado un Test de Shapiro-Wilk a cada una de ellas. En ambos casos el p-valor es inferior a 0.05. ¿Cuál es el siguiente paso a realizar?

a. Debemos aplicar el Test de Fisher-Snedecor para ver si hay que aplicar o no el Test de Mann-Whitney.

b. Debemos aplicar el Test de la t de Student de datos apareados.

c. Debemos aplicar el Test de Fisher-Snedecor y si el p-valor resulta que es inferior a 0.05 aplicar entonces el Test de  la t de Student de varianzas desiguales.

d. Debemos aplicar el Test de Mann-Whitney porque ninguna de las dos poblaciones se ajusta a la distribución normal.

5. En un estudio de comparación de dos muestras independientes de una variable cuantitativa sabemos que se ha aplicado un Test de Fisher-Snedecor de comparación de varianzas que, en realidad, no era necesario. ¿Qué afirmación seguro que no es cierta?

a. El tamaño de cada muestra es inferior a 30.

b. Una muestra se ajustaba a la normal y la otra no.

c. Las dos muestras tenían una media muestral muy distinta.

d. Las dos muestras se ajustaban a la distribución normal.

6. ¿Cuál de las siguientes afirmaciones es cierta?

a. En un contraste de hipótesis de comparación de medias la Hipótesis nula afirma que no hay relación entre las dos variables comparadas.

b. Si el p-valor es menor que 0.05 entonces se acepta la Hipótesis nula.

c. Cuanto mayor sea el tamaño de muestra más posibilidades tenemos de rechazar la Hipótesis nula.

d. Cuanta menor dispersión tengamos en un estudio de comparación de medias más difícil será rechazar la Hipótesis nula.

7. Se han estudiado las temperaturas en dos zonas distintas. Se ha aplicado un Test de Shapiro-Wilk en cada una de las dos muestras proporcionando los p-valores 0.02 y 0.01, respectivamente. Se ha aplicado el Test de Fisher-Snedecor que nos da un p-valor de 0.01. La técnica estadística a usar será:

a. Test de la t de Student de varianzas iguales.

b. Test de Wilcoxon.

c. Test de la t de Student de varianzas diferentes.

d. Test de Mann-Withney

8. Se han estudiado la presencia de un contaminante en 20 puntos de un río y en otros 20 puntos de otro río. El objetivo era detectar si el porcentaje de puntos por encima de un cierto umbral era distinto en ambos ríos. La técnica estadística a usar será:

a. Test exacto de Fisher.

b. Test de Wilcoxon.

c. Test de proporciones.

d. Test de McNemar.

9. Se han estudiado los niveles de humedad relativa en una zona donde soplan dos tipos de viento bien distintos. Se tienen los valores de cada punto estudiado en un período donde soplaba un viento y en otro período en el que soplaba el otro tipo de viento. A la resta de los dos valores de humedad relativa de cada punto estudiado se ha aplicado un Test de Shapiro-Wilk dando un p-valor de 0.35. La técnica estadística a usar será:

a. Test de la t de Student de datos apareados.

b. Test de la t de Student de varianzas iguales.

c. Test de los signos.

d. Test de Mann-Withney.

10. Se ha estudiado si hay diferencias en el nivel de conocimiento de inglés sobresaliente entre estudiantes de escuelas públicas y de escuelas privadas en un país. Para comprobarlo se ha hecho un examen común de inglés a 100 estudiantes de un tipo de escuela y a 100 del otro tipo.  En la escuela privada 4 tienen nivel de sobresaliente y en la pública 2. La técnica estadística a usar será:

a. Test de Mann-Whitney.

b. Test exacto de Fisher.

c. Test de proporciones.

d. Test de McNemar.

1b: La V de Crámer se puede calcular a cualquier tabla de contingencias.

2c: Porque si simplificamos obtenemos el modelo y=x-3 que tiene una pendiente con signo positivo, lo que es incompatible con una correlación negativa.

3d: Un p-valor mayor que 0.05 y un intervalo que contiene al 1.

4a: Porque es significativa esa correlación. El intervalo no contiene al 0.

5d: Sólo tiene una variable independiente.

6c: Al cambiar la codificación se pasa al equivalente del otro lado.

7b: Si se calcula la Odds Ratio para esos coeficientes se observa que es la respuesta correcta.

8b: Será significativa porque el intervalo no incluye al 0 y al calcular la Odds Ratio tendremos un valor mayor que 1.

9d: Indica una mayor relación.

10a: Porque la curva de la función irá de abajo a arriba.

 

1c: La magnitud de la V de Crámer en sí misma no nos indica su significación.

2d: Al tener una correlación positiva y significativa la pendiente de la recta será positiva y significativa, también. La correlación y la pendiente de la recta siguen el mismo camino siempre.

3d: Para tener una V de Crámer de 0 deberíamos tener un p-valor de 1. Para tener una V de Crámer de 1 deberíamos tener un p-valor muy pequeño. En ningún caso éste que tenemos. Tampoco tiene por qué ser 0.75. Por lo tanto, la opción es la ofrecida por d.

4d: Es evidente que no se trata de una correlación significativa porque el p-valor es mayor que 0.05. Por lo tanto, aunque tenemos una R2 buena (es mayor del 50%) no podemos hacer la regresión porque ésta sólo tiene sentido hacerla cuando la correlación entre las dos variables es una correlación estadísticamente significativa.

5a: El coeficiente de determinación me informa de la capacidad predictiva pero no sobre la significación.

6b: La correlación de Pearson cuantifica la relación entre variables cuantitativas, no cualitativas.

7d: La tabla observada será idéntica a la esperada. Tienen la misma proporción de hombre y mujeres, ambas facultades. La ji-cuadrado dará 0 y, por lo tanto, también la V de Crámer.

8c: Sabemos que únicamente las correlaciones b, c y d son significativas. Por lo tanto, la mayor de ellas es la c. Una vez se tiene un p-valor por debajo de 0.05 se trata de una correlación significativa, fiable. El que sea más pequeño el p-valor no la hace más grande a la correlación.

9c: Si la correlación es significativa también lo será la pendiente. El que, además, sea negativa la correlación indica que esa pendiente también será negativa, aunque no lo especifique.

10c: Es una buena correlación pero no significativa. Con esta información poco podemos hacer con esa correlación. Es evidente que estamos ante una muestra muy pequeña. Una correlación grande no significativa siempre va asociada a un tamaño muy pequeño.

1. En una V de Cramer no es cierto:

a. Es un valor entre el 0 y el 1.

b. Es una medida del grado de relación entre variables cualitativas.

c. Si el valor es mayor que 0.05 significa que se trata de una asociación significativa.

d. Cuanto mayor es su valor mayor relación hay entre esas variables cualitativas.

2. Si la correlación de Pearson entre dos variables es 0.7 (p<0.05) podemos afirmar:

a. La R² es del 70%.

b. La Regresión lineal que podremos hacer entre estas dos variables no sabemos si tendrá pendiente significativa hasta que no tengamos el p-valor.

c. La Regresión lineal que podremos hacer entre estas dos variables tendrá pendiente positiva pero no sabremos si es o no significativa.

d. La Regresión lineal que podremos hacer entre estas dos variables tendrá pendiente positiva y significativa.

3. Entre dos variables cualitativas la ji-cuadrado nos ha dado un p-valor de 0.75. La V de Crámer nos dará:

a. 0.

b. 1.

c. 0.75.

d. No podemos precisar qué valor obtendremos pero en ningún caso será ni 0 ni 1.

4. De una correlación r=-0.8 (p=0.1), podemos decir:

a. El tamaño muestral debe ser muy grande para tener ese p-valor con esta correlación.

b. Hay una relación significativa entre las variables estudiadas porque el coeficiente de determinación es mayor del 50%.

c. Podremos predecir con una precisión aceptable el valor de una variable a partir de la otra, porque la relación entre ellas es significativa.

d. El coeficiente de determinación es aceptable pero no podemos hacer una regresión porque no estamos ante una relación estadísticamente significativa.

5. En una Regresión lineal simple es cierto:

a. Si la R² es superior al 50% no tenemos necesariamente una relación estadísticamente significativa entre las variables de la regresión.

b. Si la correlación es r=0.5 el coeficiente de determinación del 50%.

c. Si la correlación de Pearson es significativa entonces la pendiente es positiva.

d. Si la ecuación de la recta es y=2x-3, la correlación será negativa aunque no sabremos si es o no significativa.

6. ¿Cuál de las siguientes afirmaciones no es cierta?:

a. La V de Crámer cuantifica la relación entre dos variables cualitativas.

b. La correlación de Pearson cuantifica la relación entre dos variables cualitativas.

c. Una V de Crámer nunca será negativa.

d. La ji-cuadrado nunca será negativa.

7. Los datos de una muestra obtenidos se resumen de la siguiente forma: 100 mujeres en facultades de Medicina, 100 mujeres en facultades de Historia. 50 hombres en facultades de Medicina y 50 hombres en facultades de Historia. ¿Qué afirmación es la más coherente hacer, sobre la relación entre la variable sexo y la variable ser estudiante de Medicina o Historia, con la información que tenemos?

a. La correlación de Pearson es 0.

b. La V de Cramer es mayor que 0.5

c. La V de Cramer es 1.

d. La V de Cramer es 0.

8. ¿Qué correlación es mayor?

a. r=0.9

b. r=0.3 (p=0.001)

c. r=0.7 (p=0.04)

d. r=-0.5 (p=0.000001)

9. Si estamos construyendo una fórmula matemática que nos concrete la relación entre la variable “Temperatura media anual” y la variable “Altitud” en una estación metereológica, ¿cuál de las siguientes afirmaciones es cierta?

a) Deberemos aplicar un Test de la ji-cuadrado.

b) Si la correlación entre esas dos variables es significativa tendremos una R² superior al 95%.

c) Si la correlación de Pearson es significativa y negativa la pendiente de la Regresión lineal simple será significativa.

d) Si la correlación de Pearson es negativa, la pendiente de la Regresión lineal simple será significativa.

10. Si nos dicen que tenemos entre dos variables una r=0.9 (p>0.05) podemos decir:

a) Tenemos una R² demasiado pequeña para que podamos hacer un buen pronóstico de una variable a partir de la otra.

b) La correlación es significativa porque es la R² es del 81%.

c) Esta correlación, debido a un tamaño de muestra muy bajo, nos es poco útil con la información que tenemos.

d) La correlación es significativa y la R² es del 81%, por lo que al tratarse de un coeficiente de determinación alto (mayor del 50%) podremos hacer un buen pronóstico de una variable a partir del conocimiento de la otra.