1.En la muestra (1, 1, 3, 3, 4, 5, 5, 5, 7):
a.La mediana es 3,5.
b.El primer cuartil es 3.
c. El rango intercuartílico es 3.
d.El percentil 75 es 6.
2.En un estudio oceanográfico donde relacionamos dos variables tenemos la siguiente correlación de Pearson r=-0.8 IC95%: (-1, 0.1). Podemos decir:
a.La correlación es significativa porque la R2 es superior al 50%.
b.No podemos decir nada sobre la significación porque no tenemos un p-valor.
c.La correlación no es significativa porque la correlación poblacional podría ser 0.
d.La correlación no es significativa porque el intervalo de confianza es muy amplio.
3.Estamos interesados en saber en cuántos puntos de una playa se supera un cierto nivel de un contaminante. Para ello se toman al azar 400 muestras a lo largo del río. En 20 de ellas se supera ese nivel. Un intervalo de confianza del 95% del porcentaje de puntos del río donde se supera dicho nivel es:
a.(2.82, 7.18).
b.(1.73, 8.27).
c.(3.91, 6.09).
d.(0.64, 9.36).
4.¿Cuál de las siguientes afirmaciones no es cierta?
a.La ji-cuadrado evalúa si hay relación entre dos variables cualitativas.
b.Si coeficiente de determinación es superior al 50% sólo podremos hablar de buena capacidad predictiva si el p-valor de la correlación es superior a 0.05.
c.La significación de una V de Crámer la podemos evaluar con el p-valor de la ji-cuadrado.
d.Si la tabla de contingencias observada y la tabla de contingencias esperada son iguales el p-valor será 1.
5.En cuál de las siguientes regresiones lineales simples podremos hacer peores predicciones:
a)y=0.02x+1; IC del 95% de la correlación (0.1, 0.2).
b)y=4000x+1; IC del 95% de la correlación (0.05, 0.3)
c)y=0.7x-34; IC del 95% de la correlación (0.3, 0.8)
d)y=3x+20; IC del 95% de la correlación (-0.1, 0.4).
6.Estamos tratando de asociar la presencia o la ausencia de una especie fitoplanctónica con la presencia o ausencia de una especie zooplanctónica en muestras marinas de distintas zonas del mediterráneo. Hemos codificado la ausencia con un 0 y la presencia con un 1. Hemos aplicado la ji-cuadrado de Pearson y nos da una p=0.001, podemos decir:
a.Que hay una relación significativa entre esas dos variables.
b.Que la relación no tiene suficiente capacidad predictiva.
c.Que la significación dependerá del tamaño de muestra que tengamos.
d.Que hubiéramos tenido que calcular una correlación de Pearson, no una ji-cuadrado de Pearson.
7.¿Cuál de las siguientes afirmaciones es cierta?:
a.La comprobación de la normalidad la hacemos con el test de la t de Student.
b.Si se aplica una t de Student de muestras independientes y varianzas desiguales en una de las dos muestras o en las dos no hay suficientes ajuste a la distribución normal.
c.Si dos intervalos de la media no se solapan en dos muestras independientes podemos afirmar que el p-valor en un contraste de hipótesis de igualdad de medias es inferior a 0.05.
d.Ninguna de las tres afirmaciones anteriores es cierta.
8.¿Cuál de las siguientes afirmaciones es cierta?:
a.En una regresión si la R2 es superior al 50% tenemos una relación estadísticamente significativa entre las variables de la regresión.
b. La R2 es menor del 50% no existe relación estadísticamente significativa entre las variables.
c.Una correlación estadísticamente significativa genera una R2 superior al 50%.
d.Ninguna de las afirmaciones anteriores es cierta.
9.Estamos relacionando en tres zonas distintas la presencia de cuatro especies distintas del zooplancton. Hemos aplicado una ji-cuadrado y el valor es 4.02. Entonces:
a.No podemos decir que hay relación porque 4.02 es menor que 21.02.
b.No podemos decir que hay relación porque 4.02 es menor que 12.59.
c.No podemos decir que hay relación estadísticamente significativa porque 4.02 es mayor que 3.84.
d.Podemos decir que hay relación estadísticamente significativa porque 4.02 es mayor que 3.84.
10.Un intervalo de confianza del 95% descriptivo de la variable en una muestra con media muestral 20, desviación estándar 1 y tamaño muestral de 100 es:
a.(17, 23).
b.(19.7, 20.5).
c.(19.8, 20.2).
d.(18, 22).
11.¿Cuál de las siguientes afirmaciones es cierta?
a.Si en una comparación la potencia estadística superior al 80% habrá diferencias estadísticamente significativas.
b.En el test de la t de Student de muestras relacionadas se comparan medianas.
c.En una técnica de comparación de muestras independientes con un intervalo de confianza del 95% de la resta de las medias de (-0.9, 1.12) podemos decir que el test de comparación de medias tendría un p-valor inferior a 0.05.
d.En un ANOVA de un factor con tres niveles si los intervalos de confianza de las medias son (1.2, 2.7), (1.9, 3.1) y (2.3, 3.8) el p-valor nos dará superior a 0.05.
12.En un estudio donde se quiere comparar la cantidad de un contaminante en las playas de dos poblaciones distintas tenemos 50 observaciones en cada una de las dos playas. El test de Shapiro-Wilk de ambas muestras nos proporciona un p-valor de 0.001. El test de Fisher-Snedecor nos proporciona una p=0.1. Es cierto lo siguiente:
a.Debemos aplicar el test de la t de Student para varianzas desiguales.
b.Debemos aplicar el test de la t de Student para varianzas iguales.
c.Debemos aplicar el test exacto de Fisher.
d.Debemos aplicar el test de Mann-Whitney.
13.En un estudio de comparación de dos poblaciones partimos de unos datos iniciales concretos y calculamos el p-valor con la técnica adecuada. Seguidamente aumentamos el tamaño de muestra de ambas poblaciones obteniendo la misma media y desviación estándar en ambas muestras y volvemos a calcular el p-valor. Después detectamos que la desviación estándar era más alta de la que habíamos calculado y volvemos a calcular el p-valor. Finalmente, detectamos que la diferencia de medias es más grande de la que habíamos calculado previamente y volvemos a calcular el p-valor. ¿Cuál de las siguientes es la secuencia de p-valores que podríamos tener?
a.0.54/0.23/0.25/0.12.
b.0.66/0.76/0.44/0.22.
c.0.23/0.45/0.34/0.23.
d.0.23/0.21/0.29/0.51.
14.Se analiza el porcentaje de una especie en el fitoplancton en 20 puntos del océano pacífico y 20 puntos del océano atlántico. ¿En cuál de los casos podemos decir que no hay diferencias estadísticamente significativas?
a.Pacífico: IC 95%: (23.4, 28.5); Atlántico: IC 95%: (22.4, 27.4).
b.Pacífico: IC 95%: (10.4, 12.3); Atlántico: IC 95%: (12.9, 17.2).
c.Pacífico: IC 95%: (33.5, 36.5); Atlántico: IC 95%: (37.2, 39.9).
d.Pacífico: IC 95%: (21.1, 21.1); Atlántico: IC 95%: (21.3, 21.8)
15.Hemos analizado la cantidad de biomasa en una zona en dos tiempos distintos (T1 y T2). El análisis lo han realizado tres operadores, tres analistas distintos que se quieren comparar. Cada muestra cada operario la analiza por duplicado. Los resultados son los siguientes:
¿Cuál es la afirmación no es cierta?:
a.Factor T: p>0.05.
b.Interacción: p<0.05.
c.Factor Op: p<0.05.
d.Operario con un grupo homogéneo.
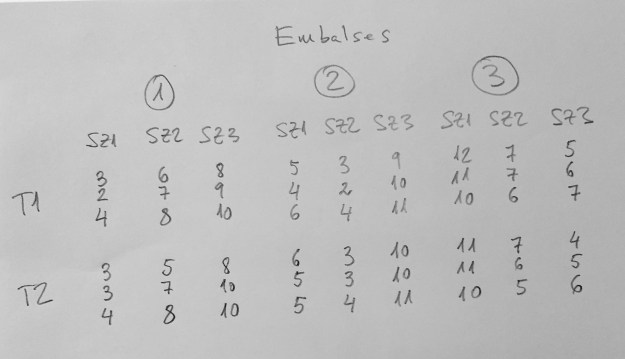
16.Supongamos que hemos tomado tres embalses españoles al azar con la voluntad de conocer la variabilidad que hay en ellos de un determinado contaminante. Tomamos tres subzonas también al azar, en cada embalse, para conocer la variabilidad interna dentro de los embalses. Queremos también conocer si las diferentes técnicas definidas para evaluar este contaminante presentan variación (hay unas quince que se han definido en la bibliografía). Para ello elegimos dos de ellas al azar y las evaluamos por triplicado en cada muestra que tenemos. Los resultados son los siguientes:
¿Qué modelo tenemos?
a.Los tres factores son significativos.
b.Sólo es significativo el factor subzona.
c.Sólo es significativo el factor Emblases.
d.Ningún factor es significativo.
17.¿Qué error podríamos estar cometiendo si al comparar dos tratamientos tenemos una potencia del 90% y el p-valor que obtenemos es de 0.2?
a.No podemos cometer error porque la potencia estadística es superior al 80%.
b.El error de tipo I.
c.El error de tipo II.
d.Ambos errores: El error de tipo I y el error de tipo II.
18.Tenemos el siguiente análisis de potencia en una comparación de dos poblaciones:
¿Qué afirmación es cierta?
a.La potencia es suficiente porque es inferior al 80%.
b.Si la desviación estándar común la cambiamos de 3 a 4 la potencia disminuirá.
c.Si las medias muestras en lugar de ser 6 y 8 fueran 6 y 5 la potencia subiría.
d.Si el tamaño de muestra por grupo pasa a ser de 50 la potencia disminuirá.
19.¿Cuál de las siguientes afirmaciones es cierta?:
a. En un ANOVA de dos factores cruzados la interacción será significativa si alguno de los dos factores lo es.
b. Un intervalo de confianza del 95% de la correlación de (-0.05, 0.05) va asociado a un p-valor de 0.05.
c. Una R2 de 50% va asociado a una correlación de 0.5.
d. Con una ji-cuadrado con un valor de 3.12 podemos decir que no tenemos una relación estadísticamente significativa, independientemente del números de filas y columnas de la tabla de contingencias.
20.Se quiere hacer un pronóstico del porcentaje de peces de una especie determinada que hay en una zona. Tenemos la sospecha, por estudios similares, que nos vamos a encontrar un valor bastante próximo al 25%. ¿Qué tamaño muestral de peces necesitamos tomar para tener un intervalo del 95% con un radio de 5%?:
a.200.
b.300.
c.675.
d.475.