Se han calculado las correlaciones entre tres variables en 20 estaciones meteorológicas y se han obtenido los siguientes valores al relacionar estas tres variables dos a dos: r=0,67(p=0,002), r=0,78 y r=0,71(p=0,0008). ¿Es significativa la correlación r=0,78 de la que no tenemos el p-valor?
La opción “c” es la única correcta. Sin la significación una correlación es casi nada. Apunta sólo una tendencia, pero nada más. La “a” no es correcta porque aunque generalmente entre temperatura mínima y máxima es verdad que suele haber una correlación positiva, esto no debe nunca constituir un “a priori” que inutilice cualquier trabajo de investigación. En Ciencia nada está relacionado hasta que no se demuestra lo contrario. La “b” no es cierta porque el hecho que no tengamos el p-valor nos dice que no sabemos la significación, no que no sea significativo el resultado. La “d” y la “e” no son ciertas y creo que ya queda explicado con lo dicho antes. Respecto a la “f” en absoluto éste es un criterio de significación.
Nos dicen que la correlación entre temperatura máxima y mínima, en una zona, es r= -0.67. Elegir la respuesta correcta:
a) Esta r es incorrecta porque entre temperatura máxima y mínima la correlación es positiva.
b) Esta r no es significativa.
c) Podemos decir poco de esta r porque no tenemos su significación.
d) Como no tenemos el p-valor la correlación no es significativa.
e) Como no tenemos significación la r es, en realidad, positiva.
f) Es significativa porque el valor absoluto de la r es mayor que 0.5.
Lo primero que hay que comprobar es si podemos usar una distribución normal como modelo de la variable que estamos estudiando. Nos dicen que la variable se ajusta bien a la Distribución normal. Como la media y la desviación estándar son, 6 y 1, respectivamente, la valoración que los consumidores hacen de ese producto sigue una distribución normal N(6, 1). Con esta distribución tenemos, pues, una maqueta, un buen dibujo de la población total de consumidores de ese producto y la valoración que ellos hacen de él.
Vamos, pues, a utilizar este modelo para calcular lo que se nos pide:
1) Como 5 es igual a 6-1, que es la media menos una desviación estándar, por encima de una valoración de 5 debe haber el 68.5 % de consumidores que hay en el intervalo que va desde la media menos una DE hasta la media más una DE, más los consumidores que hay en una de las dos colas de ese intervalo, por lo tanto, por encima de 5 tenemos: 68.5+15.75=84.25. Observemos que 15.75 es la mitad de 31.5 que es el total de lo que queda en las dos colas (los dos extremos) de la campana de Gauss en un intervalo que vaya de la media menos una DE a la media más una DE.
2) Para la segunda pregunta necesitamos saber el Error estándar (EE=DE/raíz(n)) que, en este caso, es 1/raiz(400)=0.05. Por lo tanto, tenemos una confianza del 95% de que la media poblacional esté entre 5.9 y 6.1 (este intervalo se obtiene sumando y restando a la media dos veces, ahora, el Error estándar), por lo tanto, la probabilidad de que la media esté por encima de 5 es una probabilidad muy grande, prácticamente 1.
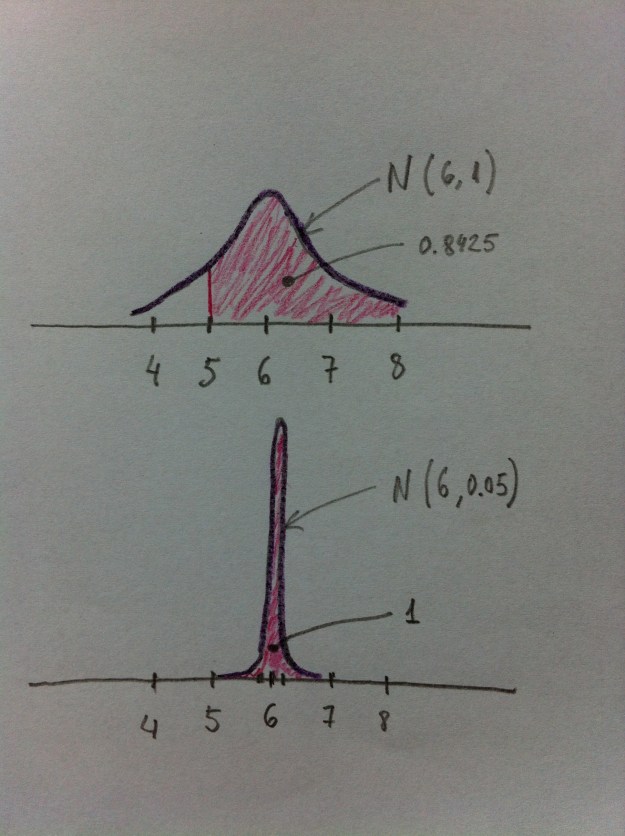
En el gráfico adjunto pueden verse las dos distribuciones normales: la de arriba, la N(6, 1), es la de la variable valoración individual de los consumidores; la de abajo, la N(6, 0.05) es la de la media. Puede verse dibujado en rojo el área que hay, por encima de 5, en ambas distribuciones.
Observemos en este problema la diferencia entre la primera pregunta y la segunda. Es importante. En la primera hablamos de valores individuales de consumidores. El 84.25% puntúan al producto por encima de 5. En la segunda pregunta hablamos de la media poblacional, no de valores individuales. La probabilidad de que la media poblacional esté por encima de 5 es prácticamente 1.
Para medir la valoración de un producto se ha hecho una encuesta entre 400 consumidores. La distribución de los valores obtenidos en la muestra se ajusta bien a una distribución normal. La media de la muestra es 6 y la Desviación estándar es 1. Calcular:
1. El porcentaje de consumidores que valoran por encima de 5.
2. La probabilidad de que la media poblacional sea mayor que 5.
Saber, realmente, cuántas personas miden más de 184 cm, en esa población, sólo lo podríamos llegar a saber si midiéramos la altura de la población entera. Esto es evidente, pero es necesario decirlo para poder situar bien lo que estamos haciendo. En Estadística pronosticamos valores, realizamos afirmaciones acerca de poblaciones inaccesibles y lo hacemos siempre a partir de información parcial de ellas, a partir de muestras.
Por lo tanto, no podemos saber el valor real solicitado, pero lo que sí podemos hacer es una estimación, podemos hacer un pronóstico de cuántos miden, en esa población, más de 184 cm. Y como la población no la tenemos construimos un modelo de ella, un sustituto de ella. Hacemos una representación mediante una maquinaria matemática.
Cuando tenemos una variable definida en una población los modelos matemáticos que dibujan, que representan, la variabilidad de esa variable, son las llamada Funciones de distribución. La más conocida y usada de ellas es la distribución normal, porque muchas variables en la Naturaleza se distribuyen según el ritmo de esa distribución. Esa fue la gran intuición que tuvo el genial Gauss ya hace siglos.
En el planteamiento de la Situación se nos dice que la muestra que tenemos se distribuye de una forma análoga a como se distribuyen las áreas bajo una campana de Gauss.
Si tomamos, pues, la distribución normal como modelo, como la media y la desviación de la muestra son 170 y 7, respectivamente, podemos decir que un modelo de nuestra población es la distribución normal N(170, 7).
Al construir el modelo es como si ya tuviéramos la población. Un poco es como cuando nos dan un plano a escala de un piso: es como si lo tuviéramos ya el piso, sin en realidad tenerlo. Podemos calcular cosas al plano y es como si le calculásemos, en realidad, al piso (metros cuadrados de una determinada habitación, etc). Pues lo mismo sucede con un modelo matemático. Le calculamos cosas y esos cálculos, si la modelización es buena, podemos proyectarlos al conjunto de la población de la que queremos decir cosas.
Observemos, ahora, que 184 es igual a la Media más dos DE (170+(2×7)=184) y como sabemos que en una distribución normal la media más menos dos desviaciones estándar cubre un 95% de los valores, a la derecha de 184 habrá un 2,5% de la población; o sea 25000 personas.
Este 25000 es, como hemos dicho, un pronóstico. Pero un pronóstico hecho mediante un procedimiento razonable, siguiendo los pasos de la modelización matemática.
Observemos que aquí el tamaño de muestra no ha jugada ningún papel. Cuanto más grande sea la muestra la estimación de la media y de la desviación estándar es más fiable, pero una vez se tiene un tamaño de muestra y una estimación de la media y de la Desviación estándar el procedimiento es el mismo, se tenga el tamaño de muestra que se tenga. Este tamaño no influye en el cálculo del pronóstico.
Como el intervalo de confianza de la media es del 95% y éste se construye con la media, que es 7, más menos dos errores estándar (en nuestro caso es 7 más menos 2) el Error estándar es 1.
Hemos de tener en cuenta que tenemos la siguiente ecuación que relaciona el Error estándar, la Desviación estándar y el tamaño de muestra: EE=DE/raiz(n). Como DE, en nuestro caso, es 5, n debe ser 25, porque EE=5/raiz(25)=1.
No necesariamente será positiva la correlación. Podría ser negativa, perfectamente. El hecho de que con una n=4 tengamos una r=0,85 que no es significativa (p=0,42) es porque todo está abierto aún. Con una muestra tan pequeña todo puede ocurrir todavía. Por esto, precisamente, el contraste de hipótesis dice que esta correlación calculada no es significativa, porque no se fía de este valor, podría ser fruto del azar del muestreo. Una muestra tan pequeña puede dar un resultado muy alejado del poblacional, del real.
Obsérvese el gráfico adjunto. A la izquierda tenemos una representación posible de nuestro punto de partida. Con cuatro valores así perfectamente podríamos tener esos valores: r=0,85(p=0,42). Pero si aumentamos el tamaño de muestra pueden pasar muchas cosas diferentes. En los dibujos de la derecha los nuevos valores, tras aumentar el tamaño muestral, aparecen con otro color. Puede ser que se confirme esta tendencia vista con cuatro valores y que la correlación acabe siendo positiva y de elevada magnitud, como se ve a la derecha arriba. Pero puede ser también que empiecen a salir valores que no sólo rompen la correlación negativa sino que incluso acaben decantando la correlación hacia un signo negativo, como podemos ver en el gráfico de la derecha abajo. Y, entre estas situaciones se pueden dar otras de intermedias.
Por esto la técnica estadística con la poca información que tenemos al principio, aunque la correlación sea grande, no se moja, no se decanta todavía. Necesita ver con más claridad, con más observaciones, para hablar de resultado significativo, estable, fiable.
Este es un buen ejemplo para entender la lógica de funcionamiento de las decisiones en Estadística y, por lo tanto, en Ciencia.
LA MATEMÁTICA Y LA ESTADÍSTICA: UNA ORQUESTA HECHA INSTRUMENTO 