1. En la muestra (1, 1, 2, 16), no es cierto:
a. La media es 5.
b. La mediana es 1.5.
c. El rango intercuartílico es 7.5.
d. El tercer cuartil es 9.
2. En una muestra de una variable que no se ajusta bien a una distribución normal nos dicen que se resume así: 20 ± 3, podemos afirmar:
a. Que el 95% de la muestra, aproximadamente, tiene valores entre 14 y 26.
b. Que el 95% de la población, aproximadamente, tiene valores entre 14 y 26.
c. Que el error estándar es 3.
d. Ninguna de las tres afirmaciones anteriores es cierta.
3. Si nos dicen que la correlación entre dos variables es 0.75 (p>0.05), podemos afirmar:
a. Que es una fuerte correlación.
b. Que es una correlación significativa y bastante fuerte.
c. Que no tenemos argumentos suficientes para desestimar que la correlación poblacional sea 0.
d. Que no es suficiente saber que el p-valor es mayor que 0.05, que necesitamos saber con precisión el p-valor para tomar una decisión.
4. Si la correlación de Pearson entre dos variables es 0.9 (p<0.05) podemos afirmar:
a. La R2 es del 90%.
b. La Regresión lineal que podremos hacer entre estas dos variables tendrá pendiente significativa.
c. La Regresión lineal que podremos hacer entre estas dos variables tendrá pendiente significativa y negativa.
d. La Regresión lineal que podremos hacer entre estas dos variables tendrá pendiente positiva pero no significativa.
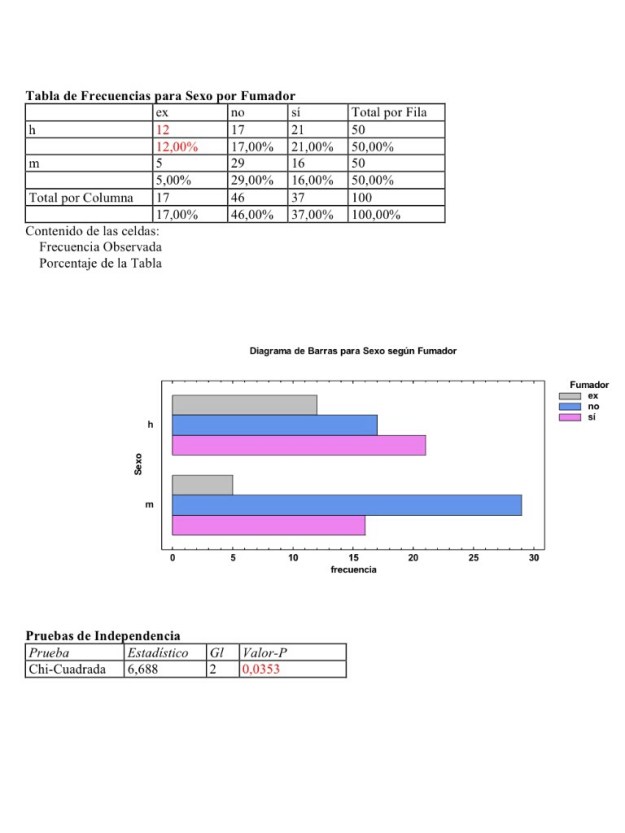
5. La V de Cramer entre dos variables cualitativas entre las cuales la ji-cuadrado nos ha dado un p-valor de 0.75.
a. Nos dará 0.
b. Nos dará 1.
c. No tiene mucho sentido calcularla porque no hay relación significativa entre esas variables.
d. En este caso calcularemos una correlación de Pearson.
6. Si queremos comparar la diferencia de medias que hay entre los hipertensos en Barcelona y Nueva York y lo hacemos tomando una muestra de 20 personas adultas en cada una de estas ciudades, donde cada una de ellas se comprueba que no se ajusta bien a una distribución normal, el test estadístico que deberemos aplicar es:
a. El Test exacto de Fisher.
b. El Test de la t de Student de datos apareados.
c. El Test de Mann-Whitney.
d. El Test de la t de Student de muestras independientes y varianzas iguales.
7. Nos dicen que han comparado la media de rentas de dos poblaciones con una muestra de cada población. Ambas muestras siguen bien una distribución normal y una estadística básica de cada una de ellas es: Población A: 15000±4000 y Población B: 13000±4000, podemos afirmar lo siguiente:
a. La diferencia de medias no es significativa porque si hacemos los intervalos de confianza del 95% de la media los intervalos se tocan porque son: (7000, 23000) y (5000, 21000).
b. La diferencia de medias sí que es significativa porque si hacemos los intervalos de confianza del 95% de la media los intervalos no se tocan porque son: (14200, 15800 ) y (12.200, 13800).
c. Para ver la diferencias de medias necesitamos saber el tamaño de las muestras que nos permita calcular el intervalo de confianza de la media de cada población para ver si se tocan o no los intervalos.
d. Estadísticamente lo único que podemos decir es que las medias de las rentas son distintas.
8. Si se quiere hacer un resumen descriptivo de una muestra de la variable cantidad de agua caída en diferentes días del año mediante una muestra como la siguiente:
(0, 0, 0, 0, 0, 0, 0, 0, 1, 2, 2, 3, 3, 4, 5, 5, 7, 8, 25, 250), la forma más coherente sería:
a. Lo haremos con los dos descriptores más habituales: la media y la desviación estándar.
b. Lo haremos con la mediana y el rango intercuartílico expresado con el primer y tercer cuartil.
c. Lo haremos con la mediana y la media.
d. Muestras tan anormales no pueden resumirse.
9. Se quiere comparar la humedad relativa entre dos zonas a partir de muestras de cada una de esas dos zonas. Se ha aplicado el Test de Shapiro-Wilk a las dos muestras y el p-valor en ambas es mayor que 0.05. Para comparar las medias o las medianas de ambas poblaciones el test más adecuado al caso será:
a. Test de la t de Student de varianzas iguales si se comprueba previamente, mediante el test de Fisher, que las varianzas no son distintas significativamente.
b. Test de Mann-Whitney.
c. El Test de proporciones.
d. El Test de la t de Student de datos apareados.
10. Si en una Regresión lineal simple entre dos variables tenemos una r=0.9 (p<0.05) y una R2 del 81% podemos afirmar:
a. Que la pendiente es significativa.
b. Que existe no hay suficiente determinación.
c. Que la pendiente podría ser positiva o negativa.
d. Poco podemos decir si no sabemos, también, el p-valor de la R2.