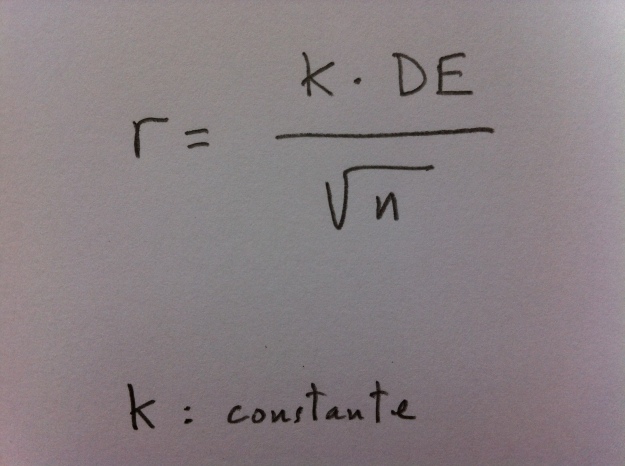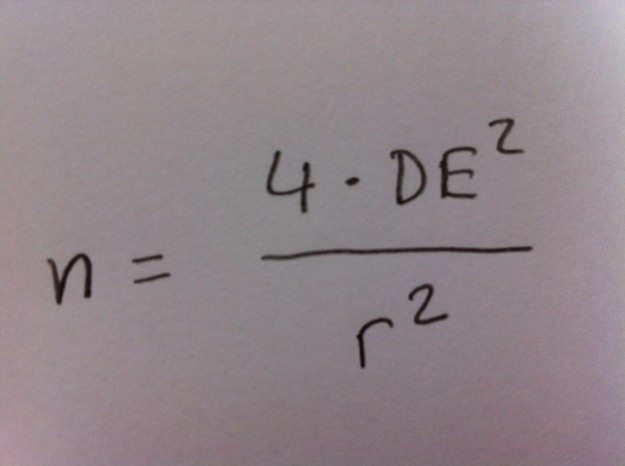Una Estadística descriptiva de estas variables cuantitativas es la siguiente:

Si hacemos una Análisis de componentes principales vemos que con las dos primeras componentes explicamos el 52,9% de la información y con tres el 71,45%:

Los coeficientes de las tres primeras componentes son los siguientes:

Como puede verse en la primera componente diferenciamos estados con con peso alto en Ciencias sociales y Servicios y peso bajo en Ciencias puras, Ciencias de la Salud y Humanidades de estados con lo contrario: peso bajo en Ciencias sociales y Servicios y peso alto en Ciencias puras, Ciencias de la Salud y Humanidades. En la segunda componente contrastamos estados con peso alto en Educación y bajo en Ciencias puras, Ingeniería y Agricultura con estados con lo contrario: peso bajo en Educación y alto en Ciencias puras, Ingeniería y Agricultura.

Observemos la posición de los Estados en un gráfico de las dos primeras componentes principales:

Finalmente, un cuadro con todas las correlaciones entre estas variables cuantitativas:

1b: Las dos Odds ratio son significativas. Una mayor que 1 (factor de riesgo) y otra menor que 1 (factor de protección.

2c: El primer cuartil es 5 (promedio de 3 y 7) y el tercer cuartil es 22. Entonces 22-5=17.

3b: El Error estándar es 5/raíz(100)=0.5. La media más menos dos EE es (19, 21).

4b: El radio del intervalo es 5. Como es un intervalo del 95% el EE=2.5, porque el radio del intervalo es dos veces el EE. Tenemos, pues, la siguiente igualdad: 2.5=10/raíz(n). Luego, para que se cumpla la igualdad n debe ser 16.

5c: Un coeficiente de determinación menor del 50% implica una precisión en los pronósticos muy mala y, por lo tanto, inaceptable.

6a: Sólo las dos primeras Odds ratio son significativas. Una OR de 10 es mayor que 0.2 porque 10 es equivalente a 0.1 y 0.2 es equivalente a 5.

7c: La V de Crámer en ningún caso puede tener valores inferiores a 0. El valor más bajo posible es 0.

8c: El valor de la ji-cuadrado en ningún caso puede ser negativa. El mínimo posible es 0. Valor que se daría si la tabla de contingencia observada y esperada fueran iguales.

9d: Dispersión y tamaño de muestra tienen una relación directa. Si tenemos más dispersión, hay más incertidumbre y necesitaremos más tamaño de muestra para ver diferencias significativas.

10c: Estamos hablando de una variable cuantitativa, de muestras independientes y ninguna de las dos se ajusta a la distribución normal (el p-valor del Test de Shapiro-Wilk es menor que 0.05 y hay que recordar a que en un test de ajuste a la normal la hipótesis nula es que existe ajuste a la distribución normal). Por lo tanto, el Test adecuado al caso es el Test de Mann-Whitney.

11b: Estamos hablando de una variable dicotómica (superar o no dicho umbral), de dos muestras independientes. Por tamaño de muestra y por valor esperado por grupo estamos bajo las condiciones de aplicación del Test de proporciones.

12d: Una correlación de Pearson puede darse acompañada de un intervalo de confianza del 95%, como sucede en cualquier pronóstico. Este intervalo de confianza lleva implícito un mecanismo que proporciona la significación estadística de esa correlación. El criterio es el siguiente: si el intervalo contiene al 0 la correlación no es significativa. Si el intervalo no contiene al 0 la correlación es estadísticamente significativa.

13a: Por supuesto que puede suceder que en un ANOVA de dos factores cruzados ninguno de los dos factores sea significativo y la interacción sí lo sea.

14c: Las comparaciones múltiples se aplican cuando se ha rechazado la hipótesis nula de igualdad de niveles de un factor en un ANOVA. Sólo en este caso tiene sentido aplicarlas esas comparaciones. Con ellas sabremos el motivo del rechazo de la hipótesis de igualdad.

15bc: (Disculpad, revisando el examen he comprobado que en esta pregunta hay dos correctas, por lo tanto, cualquiera que haya contestado a cualquiera de las dos la tiene bien, evidentemente) Si un consumo de droga tiene una Odds ratio de 5, el no consumirla tiene una Odds ratio de 0.2. El valor de 5 y de 0.2 son equivalentes. Uno al lado del riesgo y el otro al lado de la protección. Bastaría cambiar los datos de la tabla de contingencias colocando como exposición el no consumo de esa droga para obtener esa Odds ratio de 0.2.

Como la Odds ratio es 5 y es significativa un intervalo de confianza del 95% sólo tendrá valores superiores a 1, porque para ser significativa una Odds ratio dicho intervalo de confianza no debe contener al 1.

16a: Tenemos que aplicar esta ecuación, pero como el intervalo de confianza es del 68.5% la k en este caso valdrá 1. Vale 2 si el intervalo de confianza es del 95% y 3 si el intervalo de confianza es del 99.5. Luego, si la K=1 y la r=1 al despejar la n nos quedará que n es igual al cuadrado de la DE y como DE=10, entonces n=100:

17d: Por definición por encima del tercer cuartil de una muestra tenemos en la población aproximadamente el 25% de personas. Como no hay ajuste a la distribución normal la expresión de la afirmación a es incorrecta.

18d: Si una correlación es significativa también lo es la pendiente de la recta de regresión que construyamos con esa variable. Lo mismo: si una correlación no es significativa tampoco lo será esa pendiente. Son equivalentes ambos contrastes de hipótesis.

19b: Estamos construyendo un intervalo de confianza del 99.5%, lo que se consigue sumando y restando a la media 3 errores estándar. Por lo tanto, el error estándar es 1/3. Y como sabemos que EE=DE/raíz(n), tenemos la ecuación 1/3=DE/raíz(900). DE es igual a 10.

20d: El número de componentes generadas es el mismo que el número de variables originales. No tienen por qué ser positivos siempre los coeficientes de la primera componente. Si las variables son independientes el Análisis de componentes principales no nos aporta prácticamente nada. Y es cierto que si dos variables tienen fuerte correlación negativa en la primera componente saldrán con coeficientes grandes y de signo contrario. Ver, por ejemplo, en el Tema 17 el ejemplo de los datos meteorológicos: Temperatura y altitud de las comarcas tienen, lógicamente, una fuerte correlación negativa. Observad que en la primera componente sucede lo apuntado anteriormente: Coeficientes grandes y con signo distinto.

1. Sabemos que los homocigotos e4 para el gen APOE que codifica la Apoproteína E tienen una asociación con la enfermedad de Alzhéimer cuantificada mediante una Odds ratio de 5.5 (IC 95%: (4.23, 7.18)) y que los homocigotos e2 tienen una Odds ratio de 0.32 (IC 95%: (0.18, 0.45)). Es cierto lo siguiente:

a. Que para saber si la asociación es significativa nos faltaría hacer un contraste de hipótesis y tener un p-valor.

b. Que ser homocigoto e4 para ese gen es un factor de riesgo y ser homocigoto e2 es un factor de protección, respecto a la enfermedad de Alzhéimer.

c. Que no existe asociación porque los intervalos de confianza no incluyen al 1.

d. Que necesitamos saber el tamaño de muestra para saber si esta asociación es o no significativa.

2. En la muestra (-8, 3, 7, 11, 15, 22, 22, 22):

a. La mediana es 15.

b. El rango es 22.

c. El rango intercuartílico es 17.

d. El primer cuartil es 3.

3. Un intervalo de confianza del 95% de la media en una muestra con media muestral 20, desviación estándar 5 y tamaño muestral de 100 es:

a. (10, 30).

b. (19, 21).

c. (19.5, 20.5).

d. (18.5, 21.5).

4. Un intervalo de confianza del 95% de la media que sea (95, 105) que proceda de una muestra con media muestral 100 y desviación estándar 10, tiene un tamaño muestral de:

a. 4.

b. 16.

c. 25.

d. 100.

5. De una correlación r=0.45 (p=0.002), podemos decir:

a. El tamaño muestral es muy pequeño porque la correlación es pequeña.

b. No podemos decir que haya relación significativa entre las variables comparadas porque el coeficiente de determinación R² es menor del 50%.

c. No podremos predecir con una precisión aceptable el valor de una variable a partir de la otra, mediante una Regresión, porque el coeficiente de determinación R² es menor del 50%.

d. No existe correlación entre estas variables porque el p-valor es menor que 0.05.

6. ¿Cuál de las siguientes relaciones indica una relación más fuerte entre las dos variables cualitativas?

a. OR=10 (IC 95%: (8, 25)).

b. OR=0.2 (IC 95%: (0.04, 0.35)).

c. OR=25 (IC 95%: (0.8, 145)).

d. OR=0.9 (IC 95%: (0.85, 0.92)).

7. ¿Cuál de las siguientes afirmaciones no es cierta?

a. El Kappa puede ser usado como una medida del grado de concordancia entre dos observadores.

b. El Kappa tiene como valor máximo el 1.

c. La V de Crámer puede tener valores incluso negativos en casos de poca relación entre las variables.

d. Si la tabla de contingencias observada y la tabla de contingencias esperada son iguales entonces la V de Crámer valdrá 0.

8. ¿Cuál de las siguientes afirmaciones no es cierta?

a. Si una ji-cuadrado nos proporciona un p-valor menor que 0.05 indica que hay una relación significativa entre las dos variables cualitativas.

b. Si la tabla de contingencias observada y la esperada son idénticas el p-valor es 1.

c. Entre dos variables cuantitativas una ji-cuadrado negativa indica una relación inversa entre las variables.

d. Una correlación negativa y significativa entre dos variables cuantitativas va seguida de una regresión lineal simple con pendiente negativa y significativa.

9. Respecto a la comparación de poblaciones es cierto:

a. Cuanto menor tamaño de muestra tenemos más dispersión necesitamos para poder encontrar una diferencia de medias significativa.

b. Cuanta menor dispersión tenemos en las muestras más diferencia de medias necesitamos para poder encontrar una diferencia de medias significativa.

c. Cuanto más tamaño de muestra tenemos más diferencia de medias necesitamos para poder encontrar una diferencia de medias significativa.

d. Cuanto mayor dispersión tenemos mayor tamaño de muestra necesitamos para encontrar una diferencia de medias significativa.

10. Hemos de comparar dos procedimientos distintos de tratamiento para pacientes con demencia. Tomamos 100 pacientes y los repartimos al azar en dos grupos de 50 cada uno. La variable elegida para evaluar ambos tratamientos es el Mini-Mental. El Test de Shapiro-Wilk nos da, en ambas muestras, un p-valor inferior a 0.05. Debemos:

a. Aplicar el Test de Fisher-Snedecor de comparación de varianzas para saber si hemos de aplicar el Test de la t de Student de varianzas iguales o el Test de la t de Student de varianzas diferentes.

b. Aplicar directamente el Test de la t de Student de varianzas iguales sin hacer previamente el Test de Fisher-Snedecor.

c. Aplicar el Test de Mann-Whitney.

d. Aplicar el Test de la t de Student de datos apareados.

11. Hemos de comparar dos formas de rehabilitación psicológica a pacientes que han sufrido un infarto cerebral. La variable analizada es si después de un año el paciente consigue superar un umbral previamente establecido en un test psicotécnico. Se ha trabajado con 200 pacientes. 100 en cada grupo. Cada paciente recibe un único tratamiento. Después del año en un grupo un 40% consigue la rehabilitación psicológica. En el otro grupo un 50% lo consigue. Debemos:

a. Aplicar un Test de Mann-Whitney.

b. Aplicar un Test de proporciones.

c. Aplicar un Test exacto de Fisher.

d. Como entre un 50% y un 40% hay una diferencia superior al 5%, que en tanto por 1 es igual a 0.05, se trata de una diferencia estadísticamente significativa.

12. ¿Cuál de las siguientes afirmaciones es cierta?

a. Como el Test de Mann-Whitney no necesita del ajuste a la normal el criterio de decisión en él no es mediante un contraste de hipótesis.

b. En un contraste de hipótesis para evaluar el ajuste a la distribución normal la hipótesis alternativa parte como cierta inicialmente.

c. El contraste de hipótesis al trabajar y evaluar una Odds ratio tiene como hipótesis nula: OR=0.

d. La significación en una correlación de Pearson puede darse mediante un intervalo de confianza.

13. En un ANOVA es cierto:

a. Si hay dos factores cruzados podemos tener interacción significativa y que ninguno de los dos factores, individualmente, sea significativo.

b. El número de factores es el mismo al número de niveles de cada factor.

c. Si hay un único factor la interacción se interpreta entonces como relación entre niveles.

d. Si hay dos factores cruzados y los dos factores son significativos la interacción también será significativa.

4. ¿Cuál de las siguientes afirmaciones es cierta?

a. En un ANOVA de dos factores cruzados con cuatro y tres niveles, respectivamente, el número de condiciones experimentales diferentes del estudio es de (4-1)x(3-1)=6.

b. La interacción entre dos factores indica que los niveles de cada uno de los factores son distintos significativamente en las comparaciones múltiples.

c. Las comparaciones múltiples en un factor únicamente tiene sentido realizarlas si el p-valor del ANOVA previo, para ese factor, es inferior a 0.05.

d. En un ANOVA de dos factores cruzados no es posible tener un p-valor para la interacción de factores.

15. Estamos tratando de asociar el consumo de una determinada droga con un determinado trastorno psiquiátrico. Nos dicen que la Odds ratio entre los consumidores de esa droga es de 5, y que es significativa. Podemos afirmar:

a. Que un intervalo de confianza del 95% de la Odds ratio contiene al 1.

b. Que la Odds ratio asociada al no consumo de esa droga es de 0.2.

c. Que un intervalo de confianza del 95% de la Odds ratio sólo tiene valores superiores a 1.

d. Que la ji-cuadrado previa ha dado un p-valor superior a 0.05.

16. Se quiere hacer un pronóstico de la media poblacional de la concentración de un determinado neurotransmisor. ¿Qué tamaño de muestra necesitamos tomar para tener un intervalo del 68.5% de radio 1 si la Desviación estándar que tenemos en una muestra piloto es de 10?:

a. 100.

b. 1000.

c. 400.

d. 250.

17. Nos dicen que la concentración de dopamina en pacientes con Parkinson de menos de 3 años de evolución tiene una media de 20, una mediana de 15, una desviación estándar de 20, un primer cuartil de 5 y un tercer cuartil de 22, una curtosis estandarizada de 13.45 y una asimetría estandarizada de -52.24. ¿Cuál de las siguientes afirmaciones es correcta:

a. Una representación adecuada de esta muestra es 20±20.

b. Una representación breve adecuada de esta muestra es 15±20.

c. Por encima de 5 tenemos aproximadamente el 50% de la población de los pacientes de Parkinson de menos de 3 años de evolución.

d. Por encima de 22 tenemos aproximadamente el 25% de la población de los pacientes de Parkinson de menos de 3 años de evolución.

18. En una Regresión lineal simple es cierto:

a. Si la R² es superior a 50% tenemos una relación estadísticamente significativa entre las variables de la regresión.

b. Si la pendiente de la recta presenta un intervalo de confianza del 95% como el siguiente: (-3.35, -0.18), la R² será mayor que el 50%.

c. Si un intervalo de confianza del 95% de la pendiente de la recta incluye al 1 no es una pendiente significativa.

d. Si un intervalo de confianza del 95% de la pendiente de la recta no incluye al 0 entonces un intervalo de confianza del 95% de la correlación de Pearson de esas variables tampoco incluirá al 0.

19. Se quiere hacer un pronóstico de la media poblacional de la concentración de un determinado neurotransmisor. Se determina, finalmente, que para el nivel de precisión requerido y para la Desviación estándar que se ha previsto, necesitamos una n=900. El intervalo del 99.5% obtenido es (8, 10). La Desviación estándar era:

a. 15.

b. 10.

c. 20.

d. 25.

20. En un Análisis de componentes principales es cierto:

a. El número de componentes generadas en el análisis es menor que el número de variables originales.

b. Los coeficientes de la primera componente son siempre positivos.

c. Si las variables son independientes entre ellas, el Análisis de componentes principales nos aporta una muy buena reducción de dimensiones.

d. Dos variables que tienen una muy fuerte correlación negativa entre sí tendrán coeficientes grandes y con signo distinto en la primera componente principal.

1d: La Hipótesis nula en un test de comparación siempre afirma la igualdad, nunca la diferencia. Las otras tres afirmaciones son ciertas.

2a: Si se ha aplicado el test de la t de Student de varianzas diferentes es que se ha comprobado la normalidad previamente de cada una de las muestras (por lo que la respuesta b es incorrecta, porque nos estaría diciendo que no hay normalidad) y, después, hemos aplicado un test de comparación de varianzas, como es el test de Fisher-Snedecor, dando un p-valor menor de 0.05 y, por lo tanto, considerando que las varianzas poblacionales son diferentes.

3d: Si una enfermedad eleva su prevalente una técnica diagnóstica tiende a disminuir el Valor predictivo negativo. Y si una enfermedad disminuye su prevalencia una técnica diagnóstica tiende a disminuir su Valor predictivo positivo. Por lo tanto, las dos «a» y «b» son incorrectas.

4c: Entre las correlaciones signficativas la que tiene una mayor magnitud es la r=-0.7.

5a: Todas son Odds ratio significativas. Si pasamos todas las Odds ratio a la zona superior a 1, vemos que una OR=0.33 es equivalente a 3 y que una OR=0.5 es equivalente a 2. Por lo tanto, la mayor asociación es la mostrada por la OR=0.33.

6c: El error estándar es 0.5 porque es el resultado de dividir la desviación estándar (20) por la raíz cuadrada del tamaño de muestra. Por lo tanto, dos veces ese error estándar nos da el intervalo de confianza del 95% de la opción «c».

7d: El Test de Shapiro-Wilk muestra que no hay normalidad. El Test adecuado al caso es, pues, el Test de Mann-Whitney.

8c: Los datos, visulamente, de forma clara se ajustan a la distribución normal. Además el tamaño de muestra es pequeño. Todo va a favor de tener que mantener claramente la Hipótesis nula de normalidad. Es cierto que hay dos p-valores mayores de 0.05, pero uno está claramente alejado de esa frontera y el otro, por el contrario, no. En este caso la opción más lógica es elegir el p-valor superior. Observemos que si el nivel de significación lo fijáramos en 0.1 deberíamos rechazar la normalidad si tuviéramos un p-valor de 0.08.

9b: Observemos que si cogemos los valores de la OR y su intervalo de confianza y los pasamos al otro lado del 1, haciendo la división de 1 por cada uno de los tres valores implicados tenemos los valores de la opción «b»: 1/0.5=2. 1/0.36=2.77. 1/0.68=1.47.

Por otro lado, la opción «a» y la «c» son descartables por mostrar una situación de no significación que no es compatible con lo el hecho de que con el otro orden de valores sí haya significación.

La opción «d» nos da un intervalo muy próximo al 1 cosa que no es coherente con el otro intervalo. Pensemos que únicamente cambiamos de posición el elemento donde focalizamos a la hora de calcular la Odds ratio.

10c: Con una desviación estándar de 10 y un tamaño de 400 el error estándar es 0.5 y, por lo tanto, un intervalo de confianza de la media del 95% tendrá un radio de 1.

11b: Al filtrar a los pacientes de hecho lo que hacemos es aumentar la prevalencia de los que son sometidos a la prueba. Por lo tanto, al aumentar la prevalencia aumenta el Valor predictivo positivo.

12c: Hay suficiente ajuste a la normal. Sabemos que en una normal si multiplicamos la desviación estándar por 0.68 y ese valor lo sumamos y lo restamos a la media obtenemos un intervalos del 50% en torno a la media. En nuestro caso: 20×0.68=13.6. El rango será dos veces ese 13.6; o sea, 27.2.

13d: El error estándar en ambos casos es 0.5. Si construimos los dos intervalos de la media del 95% resultan: (14, 16) y (17, 19). No se tocan. Por lo tanto, hay diferencias significativas de medias poblaciones. Es con el intervalo de confianza de la media que hay que hacerlo, no con el intervalo de confianza de valores individuales.

14d: El que las cajas de los Box-Plot se toquen habla del grado de solapamiento de los valores individuales entres las dos poblaciones, pero no habla del solapamiento de los intervalos de confianza de la media. El Box-Plot no depende del tamaño de muestra. Puede aumentar mucho el tamaño de muestra y no cambiar sustancialmente la forma de ese gráfico, pero sí cambiar, y mucho, los intervalos de confianza de la media: que se van estrechando. Por lo tanto esta afirmación no es correcta.

15d: Si entre dos variables cuantitativas no existe correlación significativa no tiene sentido hacer una regresión. Además, al hacerla, la pendiente no será significativamente distinta de 0.

La «b» no es correcta porque habla del estadístico de la ji-cuadrado, del valor de la ji-cuadrado, no del p-valor.

16c: (Atención que ha cambiado la pregunta respecto a la versión anterior. Antes las respuestas eran la b, la c o la d). La precisión guarda una relación de tipo directo con el tamaño de muestra: mayor precisión mayor tamaño de muestra. Menor precisión menor tamaño de muestra.

17c: El primer cuartil es -3 porque es el promedio de -7 y 1. El tercer cuartil es claramente 3. Por lo tanto, el rango intercuartílico es 6 (3-(-3)).

18d: Si el tamaño de muestra es el mismo en dos correlaciones y una de ellas es una correlación de 0.6 y sabemos que es significativa también lo será, de significativa, una correlación que sea mayor. Podría ser dudosa la significación, sin p-valor, de una correlación que fuera menor que 0.6, pero no una mayor.

La «b» no es elegible por una razón fundamental. Es cierto que si el p-valor es inferior a 0.05 la tabla observada y la esperada son diferentes. De hecho, cualquier p-valor que no sea el 1 nos indica que la tabla observada y la esperada son distintas. Lo relevante estadísticamente es que si el p-valor es menor que 0.05 nos indica que hay relación entre las variables. Esto es lo relevante, no el que las tablas observadas y esperadas son distintas.

19b: En una tabla 2×2 el punto de referencia para aceptar o rechazar la Hipótesis nula en un test de la ji-cuadrado es 3.84, independientemente del tamaño de muestra. Este valor depende del número de filas y el número de columnas que tengamos en la tabla de contingencias, no del tamaño de muestra.

20d: Por definición de primer y tercer cuartil es obvio que por debajo del primer cuartil tendremos el 25% de la población y que por encima del tercer cuartil tendremos también un 25% de la población.

 

1. Sabemos que en un estudio de comparación de dos poblaciones se ha acabado usando un Test exacto de Fisher. No es correcto:

a. El tamaño de muestra de ambos grupos es menor que 30 ó si es mayor o igual a 30 el valor esperado por grupo, bajo la hipótesis nula, es menor de 5.

b. La variable respuesta estudiada es dicotómica.

c. Las muestras son independientes.

d. La Hipótesis nula afirma que hay diferencia entre proporciones.

2. Sabemos que en un estudio de comparación de dos poblaciones se ha acabado aplicando un Test de la t de Student de varianzas distintas. Podemos afirmar:

a. El Test de Fisher-Snedecor ha dado un p-valor inferior a 0.05.

b. Los dos Test de Shapiro-Wilk aplicados han dado un p-valor inferior a 0.05.

c. Son muestras relacionadas.

d. La variable estudiada es dicotómica.

3.¿Cuál de las siguientes afirmaciones es cierta?

a. La elevada prevalencia de una enfermedad hace aumentar el Valor predictivo negativo.

b. La baja prevalencia de una enfermedad hace aumentar el Valor predictivo positivo.

c. Las dos afirmaciones “a” y “b” son ciertas.

d. Las dos afirmaciones “a” y “b” no son ciertas.

4. ¿Qué correlación es mayor?

a. r= 0.6 IC 95%: (0.3, 0.79)

b. r= 0.5 (p>0.05)

c. r= -0.7 IC 95%: (-0.99, -0.1)

d. r= 0.2 (p<0.05)

5. ¿Qué Odds ratio es mayor; o sea, cuál indica más relación entre dos variables dicotómicas?

a. 0.33 (p<0.05)

b. 2 (p<0.05)

c. 0.5 (p<0.05)

d. 1.5 (p<0.05)

6. Si una muestra de tamaño 1600, que se ajusta bien a una distribución normal, tiene una media muestral de 40 y una desviación estándar de 20, un intervalo de confianza del 95% de la media poblacional sería:

a. (38, 42)

b. (0, 80)

c. (39, 41)

d. (39.5, 40.5)

7. Estamos estudiando dos posibles nuevos fármacos antidepresivos en pacientes con depresión mayor. Una muestra de tamaño 50 se divide en dos grupos de 25 cada uno. Los pacientes de cada uno de los dos grupos es tratado con uno de los dos fármacos. Con los valores obtenidos de la variable cuantitativa respuesta estudiada se aplica el Test de Shapiro-Wilk resultando un p-valor inferior a 0.05, en ambas muestras. El Test a aplicar será:

a. El Test de la t de Student de varianzas desiguales si el Test de Fisher-Snedecor nos da un p-valor inferior a 0.05..

b. El Test de la t de Student de varianzas iguales si el Test de Fisher-Snedecor nos da un p-valor inferior a 0.05.

c. El Test exacto de Fisher porque el tamaño de muestra por grupo es menor que 30.

d El Test de Mann-Whitney.

8. En una muestra como la siguiente: (4.2, 8.1, 9.2, 9.3, 10.1, 10.4, 10.9, 11.2, 12.4, 13.1, 13.4, 14.2, 17.5) si aplicamos un Test de Shapiro-Wilk el p-valor más lógico que podemos obtener es:

a. 0.00002

b. 0.08

c. 0.7

d. 0.02

9. Estamos tratando de asociar el consumo de un determinado producto alimenticio y una determinada enfermedad. Nos dicen que la Odds ratio entre los consumidores de ese producto y esa enfermedad es de 0.5 con un IC 95%: (0.36, 0.68). Podemos afirmar:

a. Que no hay asociación significativa porque el intervalo de confianza no contiene el 1.

b. Que la Odds ratio asociada al no consumo de ese producto sería 2 (1,47, 2.77).

c. Que la Odds ratio asociada al no consumo de ese producto sería 2 (0,47, 4.77).

d. Que la Odds ratio asociada al no consumo de ese producto sería 2 (1,04, 4.77).

10. Se quiere hacer un pronóstico de la media poblacional de la concentración de un determinado neurotransmisor. ¿Qué tamaño de muestra necesitamos tomar para tener un intervalo del 95% de radio 1 si la Desviación estándar que tenemos en una muestra piloto es de 10?:

a. 1000.

b. 100.

c. 400.

d. 250.

11. Si de una técnica diagnóstica de una determinada patología sabemos, si se aplica a la población general,  la Sensibilidad, la Especificidad, el Valor predictivo positivo y el Valor predictivo negativo, si la aplicamos ahora a pacientes filtrados previamente por tener unos determinados signos y síntomas que apuntan hacia la sospecha de una determinada enfermedad, ¿cuál de estas afirmaciones es la más posible?

a. La Sensibilidad disminuirá.

b. El Valor predictivo positivo aumentará.

c. La Especificidad disminuirá.

d. Aumentará la Sensibilidad y disminuirá el Valor predictivo positivo.

12. En una muestra con una variable cuantitativa con Asimetría estandarizada igual a 1.23 y Curtosis estandarizada de -0.98, con media igual a 120 y desviación estándar igual a  20, podemos afirmar:

a. La mediana muestral es 120.

b. Que el 95% de la población, aproximadamente, tiene valores entre 100 y 140.

c. Que el rango intercuartílico es aproximadamente 27.2.

d. Que el percentil 95 es 160.

13. En dos muestras, de tamaño 100 cada una, de dos poblaciones de una variable que se ajusta bien a la distribución normal tenemos los siguientes valores: Primera muestra: 15±5. Segunda muestra: 18±5. ¿Qué afirmación es cierta? (Cada una de las muestras es de tamaño 100)

a. Como los intervalos de confianza del 95%, de cada una de las dos muestras, se solapan no hay diferencia estadísticamente significativa de medias poblacionales.

b. Como los intervalos de confianza del 95%, de cada una de las dos muestras, no se solapan hay diferencia estadísticamente significativa de medias poblacionales.

c. Como los intervalos de confianza del 95% de la media, de cada una de las dos muestras, se solapan no hay diferencia estadísticamente significativa de medias poblacionales.

d. Como los intervalos de confianza del 95% de la media, de cada una de las dos muestras, no se solapan hay diferencia estadísticamente significativa de medias poblacionales.

14. ¿Qué afirmación, entre las siguientes, no es cierta?:

a. Cuanta menos dispersión tenemos en dos grupos a comparar menos tamaño de muestra necesitaremos para encontrar diferencias significativas.

b. Cuanta más diferencia haya entre las medias muestrales de dos grupos a comparar menos tamaño de muestra necesitaremos para detectar significación estadística.

c. Una técnica estadística de comparación de dos poblaciones aplicada a dos muestras con medias muestrales iguales, en un test bilateral nos dará un p-valor de 1, independientemente de la dispersión que tengamos.

d. Si el p-valor en una comparación de dos poblaciones es menor de 0.05 entonces las dos cajas del Box-Plot, de ambas muestras, no se solapan en ningún intervalo de valores.

15. ¿Qué afirmación, entre las siguientes, es cierta?:

a. Si la Odds ratio entre dos variables dicotómicas nos da un intervalo de confianza del 95% (0.9, 1.1) se trata de una relación significativa porque es un intervalo muy estrecho.

b. Si el valor del estadístico de la ji-cuadrado es menor que 0.05 rechazamos la Hipótesis nula de independencia de las variables cualitativas.

c. Una correlación de Pearson entre dos variables cuantitativas con intervalo de confianza del 95% (0.05, 0.85) no es una correlación significativa porque no contiene al 0.

d. Una correlación de Pearson no significativa entre dos variables es incompatible con la realización de una regresión lineal entre esas variables.

16. ¿Cuál de las siguientes afirmaciones no es cierta?

a. Un intervalo de confianza del 95% de una pendiente en una Regresión lineal simple que sea (-0.75, 0.34) nos indica una pendiente no significativa.

b. La significación de una Odds ratio puede mostrarse tanto mediante un p-valor como mediante un intervalo de confianza del 95%.

c. La precisión en la estimación por intervalos de confianza de un valor poblacional mantiene una relación inversa con el tamaño de muestra necesario.

d. Un intervalo de confianza del 99% tendrá un radio de intervalo mayor que uno del 95% de confianza.

17. Sea la muestra (-7, -7, 1, 1, 3, 3, 3, 7). Podemos afirmar:

a. El rango es 7.

b. La mediana es 1.

c. El rango intercuartílico es 6.

d. Ninguno de los tres cálculos anteriores es cierto.

18. ¿Cuál de las siguientes afirmaciones  es cierta?

a. El Test de McNemar es para muestras relacionadas cualquiera que sea la distribución de la variable estudiada.

b. En un Test de la ji-cuadrado si el p-valor es menor que 0.05 la principal conclusión estadística es que la tabla de contingencias observada y la esperada son distintas.

c. Un intervalo de confianza de la media del 95% que sea (8, 12) indica que el Error estándar es igual a 2.

d. Si la correlación de Pearson entre las variables A y B es r=0.6 (p<0.05) y la correlación de Pearson entre las variables C y D es r=0.7, si el tamaño de muestra de ambos estudios es el mismo, podemos concluir que esta última correlación de 0.7 es mayor que la de 0.6, aunque no dispongamos del p-valor concreto de esa correlación entre las variables C y D.

19. ¿Cuál de las siguientes afirmaciones es cierta?

a. Si en una regresión la R² es del 80% podemos hablar de una relación significativa.

b. Si en una tabla de contingencias 2×2 el valor del estadístico de la ji-cuadrado es menor que 3.84 no podremos decir, con la información que tenemos, que hay una relación estadísticamente significativa entre las dos variables cualitativas, independientemente del tamaño de muestra que tengamos.

c. Una Odds ratio negativa indica una relación inversa entre las variables.

d. Si existe distinta varianza, estadísticamente significativa, entre dos muestras de variables cuantitativas que no se ajustan a una distribución normal, no puede aplicarse el Test de Mann-Whitney.

20. En una muestra con curtosis estandarizada de 0.34 y asimetría estandarizada de -7.18:

a. Si la media muestral es 10 y la desviación estándar es 2 podremos decir que entre 6 y 14 tenemos el 95% de los valores.

b. La media muestral es menor que la mediana muestral.

c. Si el primer cuartil es 9 y la media muestral es 20 podemos decir que entre 9 y 20 tenemos un 25% aproximadamente de la población.

d. Si el primer cuartil es 9 y el tercer cuartil es 30 podemos decir que en la población hay, aproximadamente, los mismos valores por debajo de 9 que por encima de 30.

 

1c: Como existe ajuste a la distribución normal en ambas muestras, porque el p-valor del Test de Shapiro-Wilk es mayor que 0.05, el siguiente paso será aplicar el Test de Fisher-Snedecor y si éste es menor que 0.05, como dice esta afirmación aplicaríamos el Test de la t de Student de varianzas desiguales.

2a: El tamaño de muestra no necesariamente será menor que 30. Puede ser mayor que 30 y tenerse que aplicar igualmente este Test debido a que el número de valores esperados, por grupo, bajo la Hipótesis nula, sea menor que 5.

Podría plantearse alguna duda sobre la respuesta d: La Hipótesis nula en una comparación de proporciones siempre afirmará, necesariamente, la igualdad de proporciones. Otra cosa será si se aceptará o se rechazará, según los datos muestrales que tengamos, pero esta afirmación estará siempre, necesariamente, presente. En la Hipótesis nula siempre hay igualdad, no relación o ajuste a la distribución normal.

3d: Cuanta mayor dispersión más tamaño de muestra. Porque la Desviación estándar y el tamaño de muestra tienen una relación directa.

Atención con la respuesta c: El radio de un intervalo mantiene una relación inversa con el tamaño de muestra: menor radio precisa más muestra, pero la precisión tiene una relación directa con el tamaño de muestra: más precisión precisa de más muestra. Cuidado con este. El radio de un intervalo es menor cuanta mayor precisión queramos. Por lo tanto, radio y precisión mantienen una relación inversa.

4c: Si un factor en un ANOVA nos ha dado un p-valor superior a 0.05 no tiene sentido hacer unas comparaciones múltiples porque no habremos rechazado la igualdad de los niveles de ese factor. Las comparaciones múltiples únicamente las haremos si hay diferencias, si el p-valor de ese factor es inferior a 0.05.

5b: Si aplicamos la ecuación siguiente:

el resultado es n=100. Porque DE=10 y r=2. Se pide un intervalo de confianza del 95% que, si la media fuese 50, fuese (48, 52). Esto representa un radio de intervalo de 2.

 

1. Se está evaluando la satisfacción de pacientes ingresados en un Hospital al ser dados de alta. Se pretende comparar la satisfacción media que muestran los pacientes ingresados en dos departamentos distintos: Medicina interna y Traumatología. Se ha aplicado un Test de Shapiro-Wilk a cada una de las dos muestras. En ambos casos el p-valor es superior a 0.05. ¿Cuál es el siguiente paso a realizar?

a. Debemos aplicar el Test de Fisher-Snedecor para ver si hay que aplicar o no el Test de Mann-Whitney.

b. Debemos aplicar el Test de la t de Student de datos apareados.

c. Debemos aplicar el Test de Fisher-Snedecor y si el p-valor resulta que es inferior a 0.05 aplicar entonces el Test de  la t de Student de varianzas desiguales.

d. Debemos aplicar el Test de Mann-Whitney porque ninguna de las dos poblaciones se ajusta a la distribución normal.

2. En un estudio sabemos que se ha aplicado un Test exacto de Fisher. ¿Qué afirmación no es necesariamente cierta?

a. El tamaño de cada muestra será inferior a 30.

b. Las variables son dicotómicas.

c. Las muestras son independientes.

d. La Hipótesis nula afirma la igualdad de proporciones.

3. ¿Cuál de las siguientes afirmaciones es cierta?

a. En un contraste de hipótesis de comparación de medias lo que diga la Hipótesis nula depende de si nos interesa demostrar la igualdad o la diferencia.

b. Si el p-valor es menor que 0.05 entonces se rechaza la Hipótesis nula excepto en un Test de ajuste a la distribución normal en el que se acepta.

c. Cuanta más precisión queramos tener en un pronóstico, como la precisión es inversamente proporcional al tamaño de muestra necesitaremos menos tamaño de muestra.

d.  Cuanta mayor dispersión tengamos en un estudio de comparación de medias más difícil será rechazar la Hipótesis nula.

4. ¿Cuál de las siguientes afirmaciones no es cierta?

a. El Test de Kruskal-Wallis es apropiado para hacer un ANOVA de un factor cuyos niveles no se ajusten a la distribución normal.

b. La interacción entre dos factores evalúa si los niveles de un factor se comportan  de forma distinta al combinarse con los niveles del otro factor.

c. Las comparaciones múltiples únicamente tiene sentido realizarlas si el p-valor del ANOVA previo es superior a 0.05.

d. En un ANOVA de dos factores anidados no es posible evaluar la interacción entre factores.

5. Se quiere hacer un pronóstico de la media poblacional de la concentración de un determinado neurotransmisor. ¿Qué tamaño de muestra necesitamos tomar para tener un intervalo del 95% que, si la media muestral fuese 50, nos diese un intervalo como el siguiente: (48, 52)?  La Desviación estándar que tenemos en una muestra piloto es de 10:

a. 150.

b. 100.

c. 200.

d. 250.

SOLUCIONES:

1. ¿Hay diferencia, estadísticamente significativa, a nivel basal (a los 0 años), en cuanto al nivel de enfermedad entre los dos grupos (el grupo Placebo y el grupo Tratamiento)?

La variable del Mini-Mental es continua, las muestras que debemos comparar aquí (las dos muestras basales de los 0 años) son independientes. Debemos comprobar el ajuste a la normalidad de cada una de las dos muestras. El Test de Shapiro-Wilk nos da un p-valor de 0.0382 para el grupo Placebo a los 0 años y un p-valor de 0.3162 para el grupo Tratamiento a los 0 años. Como no se cumple que ambas muestras se ajustan a la distribución normal debemos aplicar el Test de Mann-Whitney. Este test nos da la siguiente salida de ordenador:

No hay diferencias entre las medianas (p=0.3139). Aunque tengamos una mediana de 18 y otra de 19 estas diferencias no son estadísticamente significativas. Podemos, aceptar, pues, que estamos ante dos grupos homogéneos.

Este es un test metodológicamente muy importante en muchos estudios en ciencias de la salud. La finalidad es comprobar que partimos de dos grupos homogéneos, de dos grupos con el mismo nivel de demencia.

2. ¿Hay una pérdida, estadísticamente significativa, en el grupo Tratamiento, en los dos años?

De nuevo variables continuas pero ahora muestras relacionadas. Debemos, pues, comprobar la normalidad de la variable Resta del grupo Tratamiento. El Test de Shapiro-Wilk, en este caso, nos da un p-valor de 0.0008, por lo tanto, como no hay ajuste a la distribución normal, debemos aplicar o el Test de Wilcoxon o el Test de los signos para evaluar si hay diferencias estadísticamente significativas. La salida de ordenador del Test de Wilcoxon es la siguiente:

El p-valor es de 0.000001. Observemos que la salida de ordenador nos da un p-valor de 0.0001E-2 que significa 0.0001 multiplicado por 10 elevado a menos 2 (o sea, multiplicado por 0.01). Hay, pues, diferencias significativas en los dos años.

La salida de ordenador del Test de los signos es:

El p-valor también nos indica que hay diferencias significativas.

Por lo tanto, en los dos años hay una pérdida significativa de la capacidad cognitiva de estos pacientes del grupo tratamiento. Una pérdida que puede resumirse mediante una mediana de 2, como puede verse en la salida de ordenador.

3. ¿Hay una pérdida, estadísticamente significativa, en el grupo Control, en los dos años?

De nuevo variables continuas y muestras relacionadas. Debemos, pues, comprobar la normalidad de la variable Resta del grupo Placebo. El Test de Shapiro-Wilk, en este caso, nos da un p-valor de 0.0782, por lo tanto, como hay ajuste a la distribución normal, podemos aplicar el Test de la t de Student de datos apareados para evaluar si hay diferencias estadísticamente significativas. La salida de ordenador es la siguiente:

El p-valor nos indica que hay una pérdida significativa del nivel cognitivo. Una pérdida que puede resumirse mediante la media: 3.9. La media de las pérdidas individuales es de 3.9.

4. ¿Hay diferencia, estadísticamente significativa, entre los dos grupos (Placebo y Tratamiento) en cuanto a la variable Resta; o sea, la variable Mini-Mental a 0 años-Mini-Mental a 2 años?

La variable Resta es continua, y, evidentemente, se trata de muestras independientes, hemos visto, en los apartados 2 y 3, que una no se ajusta a la distribución normal y la otra sí (p-valores del Test de Shapiro-Wilk de 0.0008 y de 0.0782, respectivamente). Esto nos obliga a trabajar con el Test de Mann-Whitney, cuya salida de ordenador, para estos datos, es la siguiente:

 

El p-valor del Test de Mann-Whitney es 0.0002, lo que nos indica que hay diferencias significativas entre las pérdidas de Mini-Mental (las variables Resta de cada uno de los dos grupos) en esos dos grupos comparados.

Por lo tanto, estamos ante un tratamiento que, desde el punto de vista estadístico, consigue una reducción significativa en la evolución de la demencia.

5. ¿Hay diferencia, estadísticamente significativa, entre ambos grupos, en cuanto al porcentaje de los pacientes que en los dos años el descenso del valor individual es superior o igual a 6?

Se trata de una variable, ahora, dicotómica y se trata, también, de muestras independientes. La duda está en si aplicar el Test de proporciones o el Test exacto de Fisher.

En el grupo Placebo hay 3 casos, entre los 30, con una pérdida de valor del Mini-Mental igual o superior a 6. En el grupo Tratamiento hay 1 caso únicamente entre los 30. Como el valor esperado bajo la Hipótesis nula es de 2 por grupo, que es menor que 5, conviene aplicar un Test exacto de Fisher. Si se aplica este test el p-valor resulta ser 0.612, lo que nos obliga a mantener la Hipótesis nula de igualdad de proporciones entre los dos grupos. Por lo tanto, las diferencias entre las proporciones muestrales de pacientes que pierden 6 ó más unidades del Mini-Mental en los dos grupos (Placebo y Tratamiento) son diferencias no estadísticamente significativas.

La salida de ordenador del Test exacto de Fisher es la siguiente:

El p-valor es 0.612, lo que nos indica que no se trata de una diferencia estadísticamente significativa.

Se ha realizado un estudio clínico con pacientes diagnosticados de Alzheimer. Se ha ensayado un tratamiento que intenta frenar el proceso de la demencia progresiva. Para ello se han seleccionado un grupo de 60 pacientes con esta enfermedad. De forma aleatoria se reparten estos pacientes en dos grupos de 30 pacientes cada uno. Durante 2 años a uno de los grupos se les da un tratamiento experimental y al otro grupo se les da un placebo. El estudio es a doble ciego. La variable estudiada para evaluar el nivel cognitivo del paciente era el Mini-Mental.

El Mini-Mental es una evaluación numérica del nivel cognitivo obtenido mediante una encuesta validada que es la siguiente:

A continuación se aporta la base de datos con los valores basales (0 años) y los valores a los 2 años de tratamiento:

GPlacebo0a=Grupo Placebo a nivel basal (a los 0 años).

GPlacebo2a=Grupo Placebo a los 2 años.

RestaP=Resta GPlacebo0a-GPlacebo2a.

GTratamiento0a=Grupo Tratamiento a nivel basal (a los 0 años).

GTratamiento2a=Grupo Tratamiento a los 2 años.

RestaT=Resta GTratamiento0a-GTratamiento2a.

GPlacebo0a	GPlacebo2a	RestaP	GTratamiento0a	GTratamiento2a	RestaT
18	14	4	17	15	2
21	16	5	20	18	2
17	13	4	21	19	2
15	12	3	23	19	4
18	13	5	22	20	2
15	12	3	19	18	1
16	14	2	19	17	2
18	14	4	18	17	1
21	16	5	20	16	4
23	17	6	15	12	3
22	21	1	16	14	2
21	18	3	18	16	2
19	13	6	21	20	1
18	14	4	20	18	2
18	13	5	16	15	1
16	13	3	16	13	3
18	13	5	23	21	2
18	11	7	24	22	2
16	13	3	22	18	4
19	18	1	19	13	6
20	15	5	18	17	1
15	13	2	17	15	2
16	12	4	17	13	4
18	15	3	19	16	3
21	16	5	17	14	3
23	19	4	16	14	2
15	14	1	19	14	5
16	12	4	20	19	1
18	13	5	15	14	1
19	14	5	19	18	1

Se pide:

1. ¿Hay diferencia, estadísticamente significativa, a nivel basal (a los 0 años), en cuanto al nivel de enfermedad entre los dos grupos (el grupo Placebo y el grupo Tratamiento)?

2. ¿Hay una pérdida, estadísticamente significativa, en el grupo Tratamiento, en los dos años?

3. ¿Hay una pérdida, estadísticamente significativa, en el grupo Control, en los dos años?

4. ¿Hay diferencia, estadísticamente significativa, entre los dos grupos (Placebo y Tratamiento) en cuanto a la variable Resta; o sea, la variable Mini-Mental a 0 años-Mini-Mental a 2 años?

5. ¿Hay diferencia, estadísticamente significativa, entre ambos grupos, en cuanto al porcentaje de los pacientes que en los dos años el descenso del valor individual es superior o igual a 6?

1d: No existen métodos de comparación entre estas tres medidas del grado de relación entre variables. Entre dos medidas significativas del mismo tipo sí que la hay, pero no entre estos distintos tipos de medidas. Cada una tiene un rango de valores posibles distinto y no hay unas pautas de comparación entre los diferentes tipos de medidas del grado de relación que aparecen en esta pregunta; o sea, entre la correlación de Pearson, la Odds ratio y la V de Crámer.

2a: Las únicas OR significativas son 0.1 y 7. Y 0.1 implica un grado de relación de 10 niveles de protección. Y 10 es mayor que 7.

3c: En esta muestra el 26 tiene 8 valores inferiores y 2 superiores. Por eso, sólo en esta muestra ocupa el percentil 80.

4b: Una OR=4 es equivalente a una OR=0.25 porque ambas suponen 4 veces riesgo ó 4 veces protección. Y 0.5 supone únicamente 2 veces protección. Por lo tanto, una OR=4 implica mayor asociación que una OR=0.5.

Una OR mayor que 1 puede ser perfectamente no significativa.

No siempre que el observado y el esperado de una tabla de contingencia no coincidan la V de Crámer valdrá 1. Valdrá 1 sólo si existe el grado máximo posible de diferencia, dado el tipo de tabla que tengamos y el tamaño de muestra que tengamos.

El índice kappa puede tener valores negativos sólo si la discordancia es muy grande.

5b: No parece haber ajuste a una distribución normal, claramente. Luego, los valores de asimetría estandarizada y curtosis estandarizada caerán fuera del intervalo (-2, 2).

6a: Si el intervalo de confianza del 95% de la pendiente no incluye al 0 se trata de una pendiente significativa. No es cierto que no lo sea, de significativa, por incluir al 1.

Las otras afirmaciones son claramente ciertas. El intervalo de confianza de la OR no incluye al 1, por lo tanto: es significativo. La correlación también lo es por tener un p-valor inferior a 0.05. Y el índice kappa indica fuerte asociación porque es casi 1.

7d: El rango es 8. La moda 3. La mediana es 3. Y el rango intercuartílico es, claramente 6 puesto que el primer cuartil es 2 y el tercero es 8.

8d: Una r=-0.6 al hacer su cuadrado tenemos que es 0.36 y al pasarlo a porcentaje se transforma en un 36%.

En una Regresión lineal simple la variable dependiente es cuantitativa, no cualitativa.

El que el p-valor sea mayor que 0.05 no es indicativo de que observado y esperado coinciden. Evidentemente, si estos coinciden el p-valor será mayor que 0.05 (de hecho, será 1), pero el que el p-valor sea mayor que 0.05 no implica que necesariamente observado y esperado coincidan.

Si un intervalo de confianza del 95% de la media es (8, 12) el Error estándar será 1, no 2, puesto que la media muestral será 10 y dos veces el Error estándar nos debe dar 2. Luego el Error estándar debe ser 1.

9d: Una OR=0.2 indica un grado de protección de 5 porque 1/0.2 es igual a 5.

La Regresión lineal simple y=3x+4 tiene pendiente claramente positiva.

La V de Crámer sólo puede tener valores entre 0 y 1.

Una ji-cuadrado no cuantifica el grado de relación que hay entre dos variables cualitativas. Valora si hay o no relación.

10c: Como ni la asimetría estandarizada ni la curtosis estandarizada caen dentro del intervalo (-2, 2) nuestra variable, en este caso, no se ajusta a la distribución normal, por lo tanto a la hora de resumirla brevemente es preferible y recomendable hacerlo mediante la mediana y el rango intercuartílico.

La afirmación «a» seguro que tiene demasiado error por el no ajuste a la distribución normal.

No tienen por qué ser iguales la mediana y la media.

Toda muestra de una variable cuantitativa tiene desviación estándar, se ajuste o no a una distribución normal. Otra cosa es cómo se interprete en función del ajuste a la distribución normal de la variable estudiada.