Este interesante artículo fue publicado en la revista Malaria Journal en el 2010.

El Abstract es el siguiente:

La región donde se realiza el estudio es la siguiente:

He elegido el artículo para comentar por el uso que hace de un análisis estadístico muy interesante: el Análisis de componentes principales. Es una técnica multivariante que combina las variables originales creando unas macrovariables (Componentes) que son diferentes combinaciones, con distintos pesos, de esas variables originales, y que explican (las primeras de esas componentes: por eso se llaman principales) la mayor parte de la variabilidad que hay entre los datos que tenemos.

Observemos, a través de la redacción de los métodos, cuáles han sido las variables utilizadas en el análisis, en este estudio. Como podemos ver variables socioeconómicas, como nos indica el título del artículo:

El Análisis de componentes principales que realizan a una muestra de tamaño 1496, da los siguientes resultados básicos:

La primera componente no explica mucho. Pero es la que explica más varianza. Explica el 20% de la variabilidad. Observemos que se ha trabajado con 11 variables originales y se obtiene 11 componentes. Lo que sucede es que son 11 componentes (11 combinaciones distintas de las variables originales) con una capacidad muy desigual de explicar la variabilidad intrínseca en los datos, como puede verse en la columna donde está la proporción de la varianza explicada por cada componente (las denomina «factores»).

Ellos han trabajado con esta primera componente, que es la que explica más varianza y que, además, tiene gran interés para lo que persigue el estudio. Suma todas las variables originales. Con pesos un poco diferentes, es cierto, pero siempre con el coeficiente positivo. Lo que nos separa las personas con buen o con mas nivel socioeconómico evaluado por esas 11 variables originales. Quien tiene más comunidades de las enunciadas en las diferentes variables es el que puntúa más en la componente. Por lo tanto, esta componente evalúa el nivel socioeconómico pesando mediante esos coeficientes las 11 variables originales.

La utilización de las componentes a partir de un estudio así puede tener muchas direcciones. Ellos exponen el uso que le han dado a la principal de esas componentes, a la primera:

Es interesante ver ese uso. Están haciendo una Regresión logística relacionando esa primera componente principal con el tener o no malaria y obtienen esas Odds ratio.

Este es un artículo del JAMA de 2014 donde se comparan dos tipos de próstesis de válvulas aórticas: biológicas y mecánicas, en pacientes de una edad intermedia donde hay controversia acerca de cuál de las dos es la mejor opción.

El estudio es interesante, desde el punto de vista estadístico, como un ejemplo de Propensity Score Analysis.

El Abstract del estudio es el siguiente:

En la siguiente tabla se muestra una descriptiva y un análisis comparativo de los dos grupos observacionales que se quiere comparar. Tenemos también el valor de diferencia estandarizada en tanto por ciento. Esto es interesante para hacer una visión unitaria de las diferencias entres ambos grupos. Pensemos que cada variable tiene escalas diferentes. Estandarizando igualamos las escalas y por lo tanto podemos ver en qué variables relativamente encontramos más o menos diferencias entre los dos grupos.

 Como puede observarse entre los dos grupos hay importantes diferencias. Diferencias que podrían generar confusión a la hora de interpretar las variables resultado. Por eso se aplica un Propensity Score Analysis. Para ver el mecanismo de esta interesante técnica puede leerse el Tema 24: Análisis de propensiones (Propensity Score Analysis).

Observemos la significación de la diferencia en primer lugar, y, después, el peso de esta diferencia, observando la diferencia estandarizada. En la edad y en la distribución por años de cirugía es donde se produce más diferencias.

Después de hacer el Propensity la tabla obtenida ahora es, con la estadística descriptiva, el p-valor de la comparación y la diferencia estandarizada es bien diferente:

Observemos ahora la enorme homogeneidad que hay entre los dos grupos a comparar. La muestra se ha reducido. Es verdad. Esto es habitual en el Propensity Score Analysis. Suele fijarse un mínimo de semejanza para incluirse y esto provoca que algunos casos no tengan un control lo suficientemente próximo.

Un aspecto técnico a destacar en esta comparación entre los dos grupos es que estos autores han llevado al extremos máximo posible la idea de matching, la idea de apareamiento, del Propensity Score Analysis, porque las dos muestras obtenidas de tamaño 1001 no las trabajan como muestras independientes sino como muestras apareadas, como si en lugar de tener 2002 individuos tuviéramos 1001 a los que se les ha puesto dos prótesis al mismo tiempo. Esto es discutible. En principio este análisis sirve para homogeneizar grupos pero no para hacer este salto metodológico tan importante.

Una vez se tiene esos dos grupos ahora ya es cuestión de compararlos. Con toda la tecnología habitual en este tipo de estudios en Medicina: Curvas de supervivencia. Número de incidencias. Etc. Como puede verse a continuación:

 

Como puede verse en estos gráficos y en las conclusiones del estudio en 15 años de seguimiento de estos pacientes no hay diferencias en la mortalidad ni el la incidencia de ictus y la única diferencia es que las prótesis biológicas tienen una mayor incidencia de reoperaciones y las mecánicas una mayor incidencia de hemorragias mayores.

Este es un artículo importante publicado en el New England Journal of Medicine.

El Abstract es el siguiente:

Interesa destacarlo por la técnica adecuada al caso que utilizan para analizar los datos.

Como puede verse el objetivo es ensayar un nuevo y revolucionario método para enfrentarse a la infección digestiva de Clostridium difficile: mediante infusiones duodenales de donantes con infección cronificada por esa especie bacteriana.

Una descriptiva de los grupos a comparar es la siguiente:

Los tamaños de muestra empleados son bajos, ciertamente. Sin embargo, los resultados son muy espectaculares, como puede verse a continuación:

 

La técnica adecuada al caso, en este estudio, como puede verse en el cuadro del Tema 14, es el Test exacto de Fisher. Son dos poblaciones, porque las comparaciones se hacen dos a dos, como puede observarse, la variable estudiada es dicotómica (Hay o no curación sin recaída) y el tamaño de muestra por grupo es menor de 30 en todos los casos. En el cuadro importante comentado en el Tema 14 podrá verse que siguiendo estos pasos llegamos al Test exacto de Fisher. Es la técnica adecuada al caso, la que optimiza la decisión de si rechazar la Hipótesis nula de Igualdad de proporciones o, por el contrario, rechazarla y pasar a la Hipótesis alternativa que afirma que hay diferencia entre las proporciones.

El gráfico anterior nos muestra cuáles son las diferencias significativas, nos marca los p-valores que son menores que 0.05 y a través de los cuales, por lo tanto, podemos decir que las diferencias de proporciones muestrales obtenidas son diferencias significativas; o sea, son diferencias que pueden generalizarse a nivel poblacional. En este caso, esta generalización poblacional es de futuro. Se está diciendo, en realidad, que si se aplicara entonces los pacientes tratados con esas infusiones conseguirían índices de curación sin recaída superiores a los obtenidos con el tratamiento antibiótico convencional, con una probabilidad de equivocarse menor del 5%.

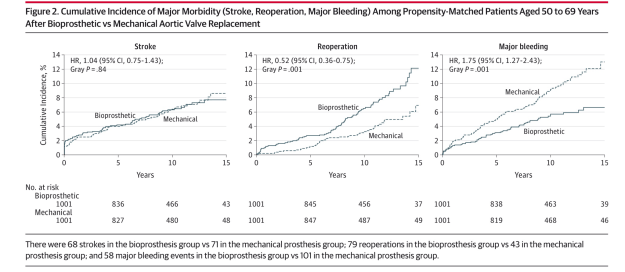
Este es un artículo muy interesante para ver una aplicación del Propensity Score Analysis en Medicina.

En este artículo se comparan los resultados obtenidos por cirugías cardiovasculares en pacientes HIV respecto a pacientes no HIV.

Comparaciones de este tipo constituyen retos muy habituales en Medicina. Se trata de estudios llamados observacionales, estudios donde se comparan dos grupos que han sido configurados de forma natural y espontánea, previamente al análisis estadístico que se efectúa. No se trata, por lo tanto, de estudios experimentales donde, de una forma organizada, se van repartiendo tratamientos diferentes a un conjunto de pacientes, dentro de unos parámetros previamente prefijados.

Los estudios observacionales son mucho más sencillos de hacer porque representa aprovecharse del esfuerzo clínico previo de mucha gente. Los resultados los tienes ya, sólo hace falta ponerte a analizarlos. Sin embargo, son más débiles en cuanto a nivel de evidencia de las conclusiones que se obtienen de ellos. Son muchos los posibles factores que pueden estar enmascarando, confundiendo e introduciendo sesgos en los resultados obtenidos mediante este tipo de estudios.

Los llamados estudios de Casos y Controles son un tipo muy frecuente de estos estudios observacionales. De hecho, el estudio presentado en este artículo podría ser llamado perfectamente así, aunque no es un arquetipo de lo que sería un estudio de Casos y Controles en Medicina, evidentemente. En los estudios de Casos y Controles se estudia la asociación de esos dos resultados con diferentes factores, con diferentes exposiciones a un riesgo o a un factor de protección. En este estudio, de hecho, los Casos y los Controles son las variables resultado: mortalidad y diferentes complicaciones. Y, fundamentalmente, el ser HIV positivo o negativo es el factor de exposición estudiado. Se quiere ver si ser HIV positivo es un factor de riesgo en los pacientes que han sido sometidos a una intervención quirúrgica cardiovascular.

Además, en este estudio, como se verá a continuación, se intenta evitar todos estos problemas presentes habitualmente en los estudios observacionales mediante la aplicación del Propensity Score Analysis. Esta técnica trata de evitar confusiones externas homogeneizando lo más posible los dos grupos a comparar.

El Abstract del artículo es el siguiente:

Suele ser habitual en este tipo de estudios que haya una elevada desproporción de Controles respecto a los Casos que se tienen registrados en la muestra. Es justo lo que sucede en la muestra con la que se trabaja inicialmente en este estudio, como puede apreciarse perfectamente en las tablas siguientes.

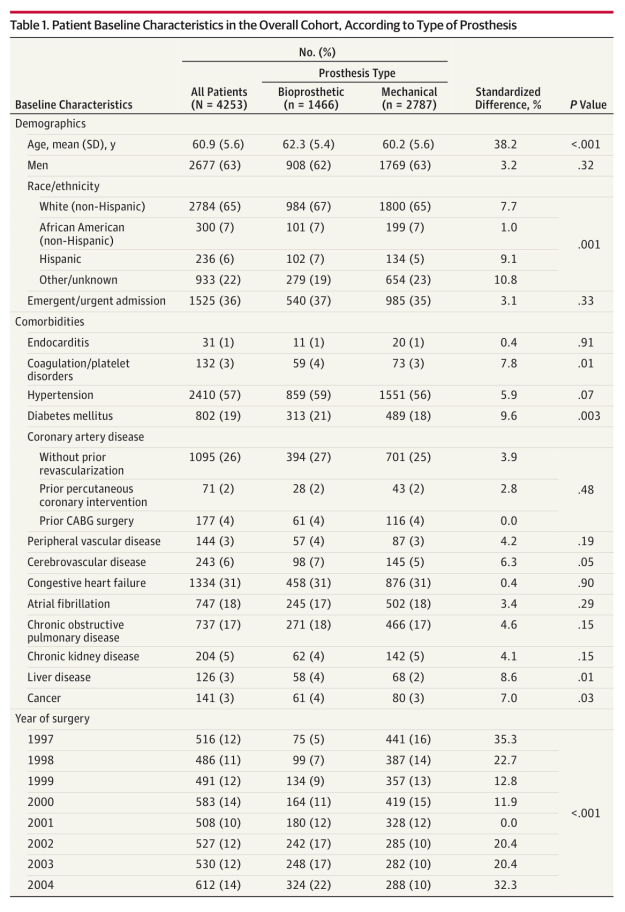
Veamos, en primer lugar, la comparación de los dos grupos del estudio en una serie de variables demográficas:

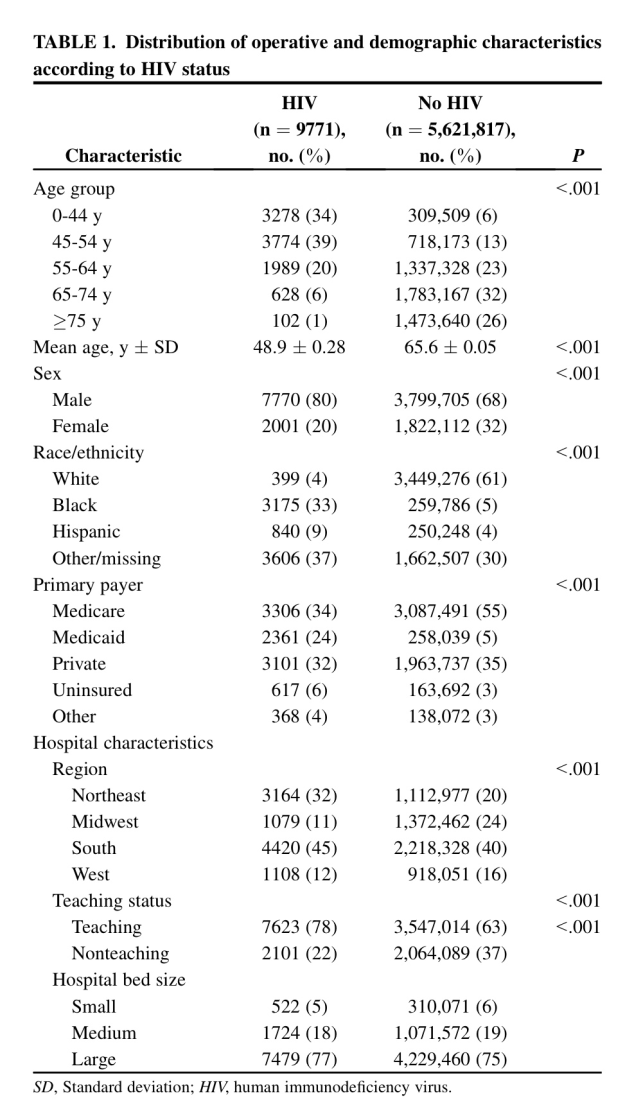
Como puede verse hay enormes diferencias entre ambos grupos en cuanto a esas variables demográficas. Todas las variables excepto la Edad se comparan mediante un Test de la ji-cuadrado. La variable edad se compara con un Test de la t de Student de muestras independientes y varianzas iguales. Son las técnicas adecuadas al caso según puede verse a partir del cuadro comentado con detalle en el Tema 14: Comparación de dos poblaciones.

Sin embargo, observemos un error que hay en la variable Edad. Nos dicen que se da la media y la Desviación estándar (SD). Es como se suele presentar la descriptiva de una variable continua que se ajuste suficientemente bien a la distribución normal (Ver el artículo La Estadística descriptiva en Medicina).  Evidentemente no puede ser. Es imposible que se trate de la Desviación estándar. Las edades serían muy similares, demasiado similares, dentro de cada grupo. Pensemos que si hay ajuste a la normal sumar y restar dos veces la desviación estándar nos cubriría el 95% de los valores. En el caso de los No HIV deberían tener, prácticamente todos, los 5.621.817 de la muestra, 65 años. Podemos pensar, entonces, que se trata del Error estándar. Suele ser habitual confundir Desviación estándar con Error estándar. Pero, tampoco. Sabiendo el Error estándar y el tamaño de muestra podemos calcular la Desviación estándar, a partir de la relación que conocemos entre esos dos cálculos muestrales (Ver el Tema dedicado a los Intervalos de confianza):

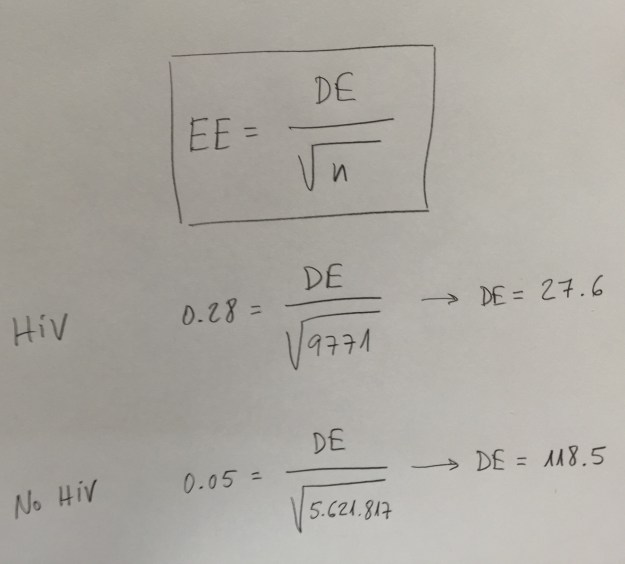
El Error estándar (EE) es igual a la Desviación estándar (DE) dividido por la raíz cuadrada del tamaño de muestra n. El Error estándar es la Desviación estándar de una predicción. La Desviación estándar es una medida de dispersión de las variables y el Error estándar es una medida de dispersión de predicciones.

En todo caso, lo que es también claro es que estas desviaciones estándar de las variable Edad en el grupo HIV y en el grupo No HIV tampoco pueden ser. Serían excesivas. En todo caso, si admitimos que son correctas debemos admitir, entonces, que en absoluto se ajustan a una distribución normal.

Bueno, a efectos del estudio, lo que parece evidente, y es lógico que sea así, es que hay una enorme diferencia en cuanto a edades de los dos grupos que estamos comparando.

En la tabla siguiente se analizan más diferencias entre ambos grupos. Ahora son variables que evalúan las comorbilidades que presentan ambos grupos de pacientes:

Diferencias muy importantes, pues, en cuanto a las comorbilidades. Se trata, pues, como es lógico, de perfiles de pacientes muy diferentes, en cuanto a la clínica, los que estamos comparando en este estudio.

Más diferencias, aún, nos muestran los autores de este artículo. Ahora en cuanto al tipo de cirugías cardiovasculares practicadas en ambos grupos:

Por lo tanto, comparar el éxito o fracaso de la cirugía cardiovascular, en ambos grupos, puede quedar perfectamente confundido por algunas de esas variables que presentan estas enormes diferencias entre ambos grupos. Este es un problema evidente en este tipo de estudios.

No podríamos ahora dedicarnos a evaluar variables resultado, variables que evalúen los resultados de las cirugías cardiovasculares entre estos dos grupos porque son dos grupos, tal como los tenemos ahora, y como lo hemos podido apreciar perfectamente en las tablas anteriores, muy diferentes y difícilmente comparables. Las diferencias que viéramos podrían ser atribuibles no al elemento que queremos comparar (ser o no HIV) sino a otros elementos que harían sesgar nuestras conclusiones.

Observemos una comparación de unas variables resultado en estos dos grupos tal cual, sin intervenir tratando de homogeneizarlos:

Estas diferencias pueden ser, repito, explicadas no únicamente por el hecho de ser o no HIV los pacientes, sino por la gran diferencia que hay en otras variables que actuarían confundiéndose con las variables resultado y, por lo tanto, confundiéndonos, haciéndonos pensar que las diferencias son por ser pacientes con y sin HIV y, en realidad, ser atribuibles a otras causas. Este es el significado que habitualmente damos a las llamadas variables confusoras en un estudio.

Pues bien, necesitamos intervenir para evitar estas confusiones. El Propensity Score Analysis es una técnica que intenta evitar este problema. Trata de igualar los grupos a comparar. Y lo hace generando lo que se llama un Propensity Score a cada paciente del estudio. Tanto a los casos como a los controles. Este Score se calcula mediante una Regresión logística múltiple. Una Regresión logística donde la variable dependiente dicotómica es la variable ser Caso o ser Control. Por lo tanto, como en toda Regresión logística se obtiene una probabilidad de ser Caso o de ser Control en función de unos valores de las variables independientes utilizadas. La técnica lo que hace entonces es asociar puntos por Score próximo (Lo que suele denominarse un Matching, un apareamiento). Puede fijarse una ventana, un umbral a no superar. Los Casos que no tengan un Control lo suficientemente cercano serán rechazados para el estudio. Paciente con un Propensity Score próximo será porque serán próximos los valores de las variables que habremos utilizado como variables independientes. Esta es la forma automatizada de buscar pacientes que aunque son de los dos grupos presentan perfiles muy similares de las variables elegidas para la homogeneización.

El gráfico que aportan los autores de este estudio y que a continuación se muestra es genial. Observemos una medida, variable por variable contemplada en el Propensity Score Analysis, de una diferencia estandarizada, entre ambos grupos, antes y después del Propensity.

¿Qué es y por qué se usa una diferencia estandarizada? Se hace para evitar deformaciones posibles debidas a la escala. No es lo mismo trabajar, por ejemplo, con hematíes que con creatinina. De forma absoluta no son comparables las diferencias de medias de ambas variables en ambos grupos. Lo mismo sucede al comparar porcentajes. Estandarizar una variable en Estadística significa transformarla para que tenga media 0 y desviación estándar 1. Así todas las variables estandarizadas son comparables. En nuestro caso, si la diferencia de medias o de porcentajes entre los dos grupos lo dividimos por la desviación estándar que tenemos también lo estamos estandarizando. Que es lo que, en realidad, se hace aquí. Así todas las variables son más comparables en cuanto a la diferencia que hay entre los dos grupos:

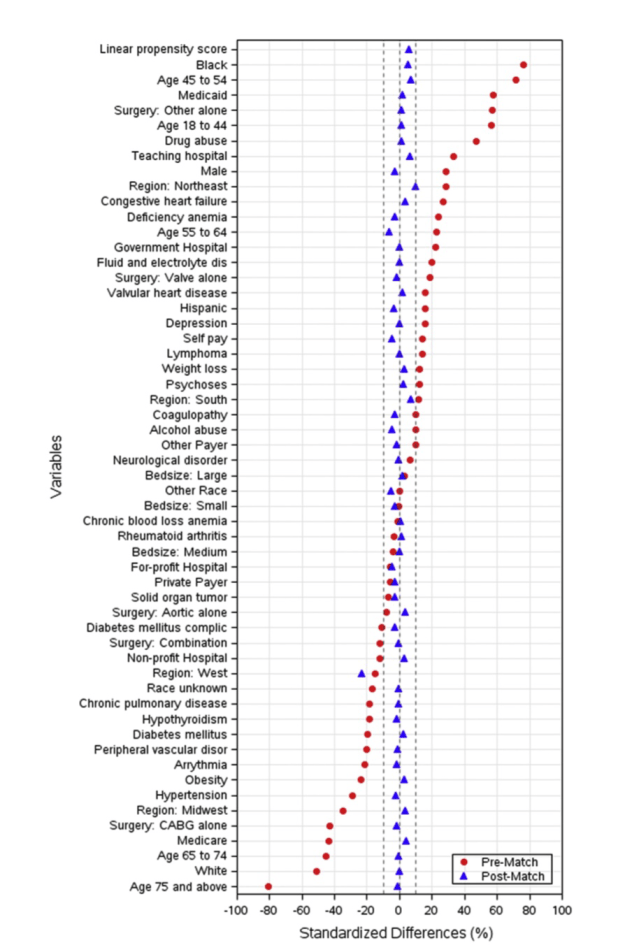
Veamos un ejemplo de esto que acabamos de ver. Tomemos las dos primeras variables de la Tabla 2: La hipertensión y el fallo cardíaco: Si restamos los porcentajes vemos que en la hipertensión tenemos una diferencia de un 15% entre ambos grupos (Un 42% en HIV y un 57% en No HIV). En fallo cardíaco la diferencia es sólo de un 5.1% (Un 6.5% en HIV y un 1.4% en No HIV). Es obvio que un 15% es mucho mayor, en valor absoluto, a 5.1%, pero si lo relativizamos respecto a la dispersión que tenemos al movernos en torno a un porcentaje de 42 al 57% o respecto a la dispersión que tenemos en torno al 6.5% y el 1.4%, la cosa cambia. Hay mucha más dispersión en una variable que está próxima al 50% que en una que está próxima al 4%. Hay más saltos de un valor a otro en la primera y, por el contrario, más monotonía en la segunda. Esto debe ponderarse. Miremos cómo quedaría:

En valor absoluto tenemos una diferencia del 15% en hipertensión y un 5.1% en fallo cardíaco. Sin embargo, al estandarizar la diferencia, estamos hablando de un 30% y un 26%, valores mucho más igualados.

En el gráfico anterior podemos ver cómo han cambiado las diferencias estandarizadas entre ambos grupos al realizar el Propensity Score Analysis. Nunca había visto hasta ahora un gráfico que lo ilustrara tan bien. Antes del Propensity hay grandes diferencias, a veces a favor de un grupo, a veces en contra. Después del Propensity se ha conseguido homogeneizar los grupos. Se están comparando grupos más homogéneos, se está eliminando confusión, sesgos.

Una vez se han encontrado los dos grupos ahora se trata, pues, de compararlos.

Observemos, no obstante, antes, que los dos grupos son de 1633. No están todos los HIV. Seguramente porque ha habido muchos casos que no han tenido un buen control apareado lo suficientemente próximo.

En las tablas siguientes se comparan esos dos grupos, ahora ya homogeneizados. Se ha seleccionado, pues, entre los No HIV un grupo homogéneo al grupo HIV. Y esto nos permite ver que en cuanto a las variables resultado estudiadas estos dos grupos homogenizados ya no presentan diferencias significativas, excepto en cuanto a la necesidad de transfusiones, donde hay un leve aumento de riesgo en los pacientes HIV, como se comenta en las conclusiones del Abstract.

En la siguiente tabla se calculan las Odds ratio ajustadas (Ajustadas por la homogeneización que supone el Propensity) para unas variables resultado donde se mide la cantidad de asociación, si es que la hay significativa, con el ser o no HIV:

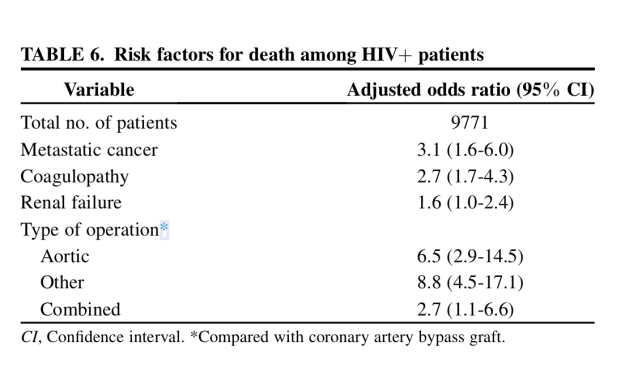
En la tabla siguiente también aportada por los autores de este artículo se aprovecha la información de todos los casos que se tiene de pacientes con HIV operados para analizar factores asociados con la mortalidad:

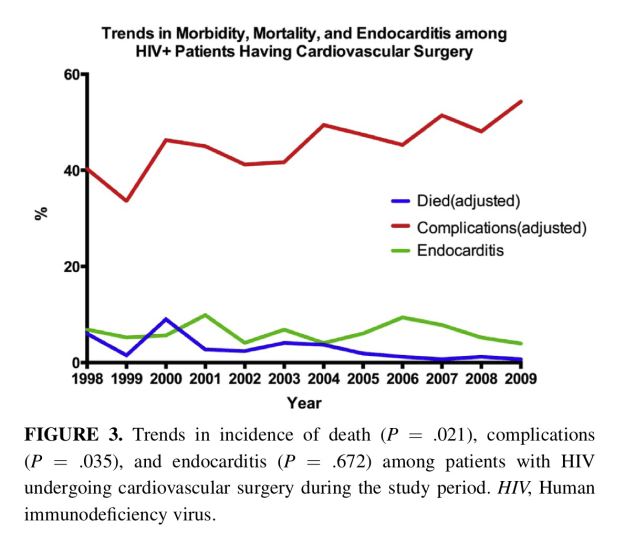
Finalmente el estudio nos aporta un gráfico de la evolución a lo largo del tiempo de una serie de variables de interés (Mortalidad, Complicaciones y Endocarditis) detectando si hay una pendiente estadísticamente significativa. Como puede verse, y el p-valor así lo certifica, hay una pendiente significativa y negativa en la Mortalidad, significativa y positiva en las Complicaciones y no hay pendiente significativa en la incidencia de Endocarditis.

 

 

Este es un artículo clásico en Medicina, aparecido en 1984 en el New England Journal of Medicine.

El Abstract es el siguiente:

Es un artículo sencillo pero excelente para establecer un primer contacto con la Estadística aplicada a las ciencias de la salud.

El objetivo básico es comparar el nivel de densidad ósea entre un grupo de mujeres diagnosticadas de Anorexia nervosa y un grupo control; o sea, un grupo equivalente de mujeres que no tienen el diagnóstico de ese trastorno de la alimentación.

Al diseñar esos dos grupos el estudio también clasifica a las mujeres, de ambos grupos (anoréxicas y controles), en dos nuevos grupos: según su tipo de vida pueda considerarse de bajo o de alto nivel de actividad. Es verdad que el nivel de actividad no es una variable dicotómica, hay muchos niveles distintos de grado de actividad, sin embargo, los autores del estudio lo acaban transformando en esos dos grupos, estableciendo presumiblemente un determinado nivel umbral.

En una tabla del artículo se describen las características de las 18 pacientes con Anorexia nervosa. Esto es interesante como introducción a lo que una base de datos en estudios de este tipo. Es una matriz donde las filas son los pacientes y las columnas las distintas variables estudiadas:

Como puede verse ya en el Abstract, se nos proporciona resúmenes descriptivos por grupo: se nos da la media y la desviación estándar de la densidad ósea en cada uno de los dos grupos principales del estudio (anoréxicas y controles), expresado como es habitual con el más/menos.

En este artículo aparece también la noción de p-valor, como medida de la significación. Concepto nuclear en Estadística y en cualquier Ciencia, por supuesto.

La finalidad del estudio, como ya hemos dicho, es comparar esos cuatro grupos comentados. Para comparar los cuatro grupos aplican un Test de Kruskal-Wallis y obtienen un p-valor inferior a 0.05. Por lo tanto, hablan de diferencias estadísticamente significativas entre esos cuatro grupos. Lo que significa que podemos inferir, con poca probabilidad de error de equivocarnos, que esas diferencias deben existir a nivel poblacional, no únicamente a nivel muestral.

A continuación hacen comparaciones dos a dos entre los cuatro grupos, que es lo más trascendente del estudio. Explicando, por cierto, muy bien qué técnica de comparación aplican en cada momento. Lo hacen siguiendo los conceptos que están presentes en el Tema 14: Comparación de dos poblaciones.

La presentación de los resultados se hace, desde el punto de vista de un profesor de Estadística, de forma genial. Es una auténtica clase de Estadística, como se puede ver a continuación:

Viendo esta tabla poco le queda para decir a un profesor de Estadística. De hecho, lo que consigue hacer visualizar un artículo como éste es extraordinario. Artículos como éste se encuentran a faltar cuando uno ve actualmente algunos artículos que los resultados cuestan ser interpretados incluso para los que nos dedicamos desde hace muchos años a la Estadística.

Observemos que viendo las cuatro muestras parece muy claro que a la hora de compararlas podremos usar técnicas paramétricas. Ninguna de ellas es claramente anormal (en Estadística anormal significa que no se ajusta a la campana de Gauss). Por lo tanto, podremos aplicar el Test de la t de Student, que es lo que hacen. Y las varianzas son también del mismo orden, por lo tanto, parece lógico aplicar el Test de la t de Student para varianzas iguales.

Observemos que marcan dos comparaciones como diferentes significativamente. La que hay entre mujeres anoréxicas y controles a bajo nivel de actividad. Y la que hay en mujeres anoréxicas entre las de bajo y alto nivel de actividad. Esto es lo que les lleva a la conclusión del estudio que aparece en el Abstract del artículo.

El artículo también comenta que no se ha encontrado relación entre el nivel de estradiol de la paciente y la densidad ósea. Habla de la r, que es la correlación de Pearson. No encuentra relación.

Es importante este artículo, pues, como se puede ver, porque en él vemos integrados las tres familias de técnicas estadística: descriptivas, de relación y de comparación, comentadas en el Tema 1. Hay descripción, hay inferencia. Hay evaluación de posibles relaciones. Hay comparación entre grupos.

Repito: un magnífico ejercicio para introducirse en el mundo apasionante de la Estadística y su relación con las ciencias de la salud.