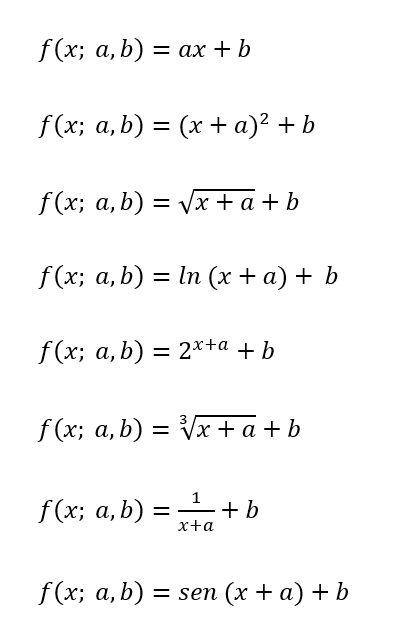Conjuntos:

Un conjunto es una reunión, bajo cualquier criterio, de una serie de entidades.

Subconjunto es un conjunto que está incluido en otro conjunto.

En forma gráfica típica:

Los conjuntos más usuales en Matemáticas son:

Conjuntos de números (Naturales, Enteros, Racionales, Reales y Complejos)

Conjuntos de matrices

Conjuntos de funciones

Producto cartesiano de dos conjuntos:

El producto cartesiano de dos conjuntos es un conjunto formado por todas las parejas posibles de elementos de los dos conjuntos, respetando el orden: el primer elemento es del primer conjunto y el segundo elemento lo es del segundo conjunto.

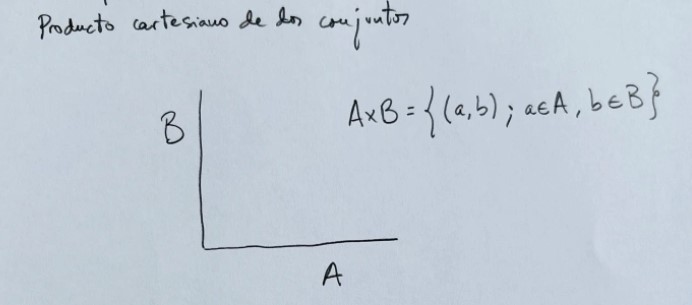
Ejemplos: El plano es un producto cartesiano. En una clase se puede establecer el producto cartesiano de ella por ella misma.

Conjuntos de números:

Veamos la posición relativas de los diferentes conjuntos de números que veremos:

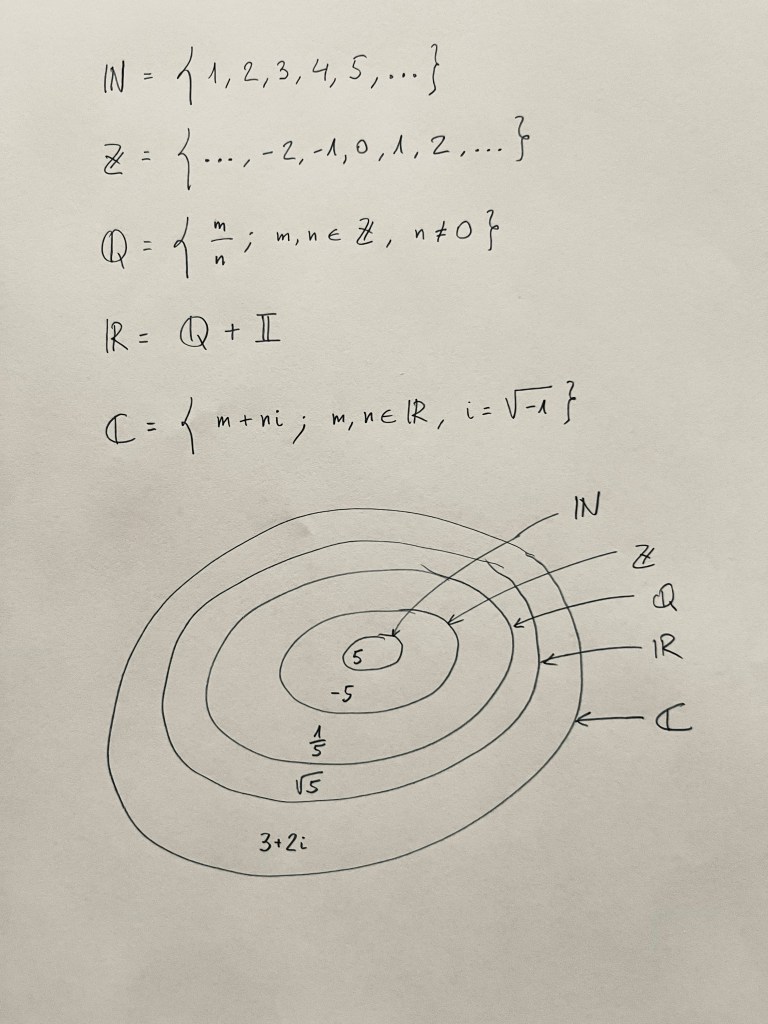
Números naturales:

Leopold Kronecker decía en el siglo XIX que los números naturales son los que creó Dios y los demás tipos de números eran creación humana.Tradicionalmente representados por una N.

Nos sirven como modelos de la cantidad de entidades que vemos, que manejamos.

Números enteros:

Son los números naturales, más los naturales negativos y el cero.

Tradicionalmente representados por una Z.

Nos sirven, entre otras muchas cosas, para modelizar las deudas, las temperaturas por debajo de cero, los pisos por debajo del suelo.

Números racionales:

Son los denominados, también, fracciones o, antiguamente, los números quebrados.

Tradicionalmente representados por una Q.

Nos sirven para modelizar cosas como partes de un todo. Cuánta pizza toca a cada uno, cuánta parte llevamos pagada, etc.

Números reales:

Es la suma de los números racionales y de los denominados números irracionales.

Los irracionales son los números que no son racionales; o sea, números que no se pueden expresar en forma racional.

Tradicionalmente representados por una R.

Nos sirven como modelo de muchas cosas. Por ejemplo, para calcular la longitud de la diagonal de un cuadrado de lado 1. También para saber la relación que hay entre el radio y el perímetro de una circunferencia cualquiera.

Números complejos:

Son unos números que representan la suma de los reales más unos números que tienen la denominada componente imaginaria.

Tradicionalmente representados por una C.

Son modelo de situaciones más sofisticadas. Una por ejemplo: todos recordamos aquellas ecuaciones de segundo grado que al aplicar la regla para encontrar las soluciones aparecía la raíz cuadrada de un número negativo. Decíamos, entonces, que no había solución, que era una ecuación sin solución. Pues, aquellas ecuaciones tienen solución en el conjunto de los números complejos. En ciertos campos del conocimiento aparecen problemas que se plantean en forma de ecuación y cuya solución son números complejo.

Relaciones:

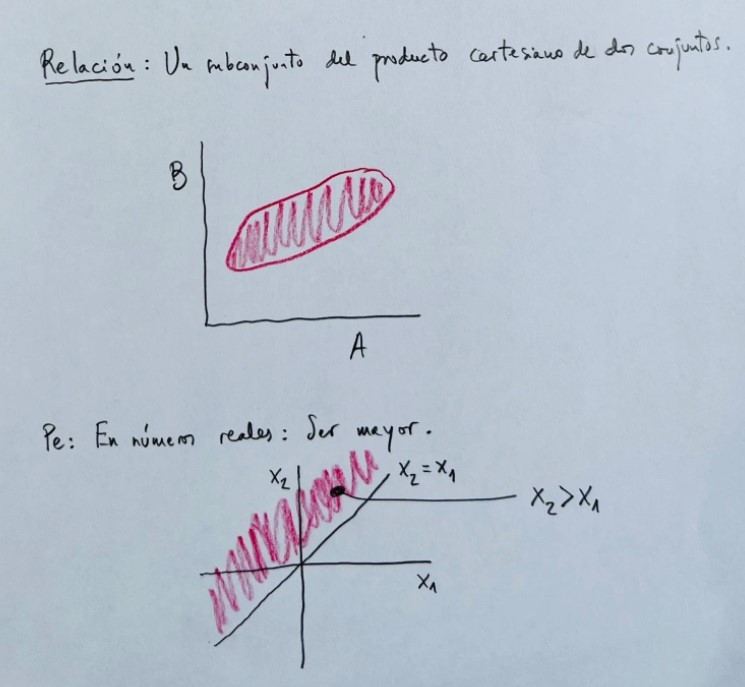
Ejemplos de relaciones:

1)Ser mayor o igual.

2)Ser divisor de un número.

3)Regiones factibles.

4)En una clase, haber hablado, tener el teléfono, haber estudiado la secundaria en la misma escuela, etc.

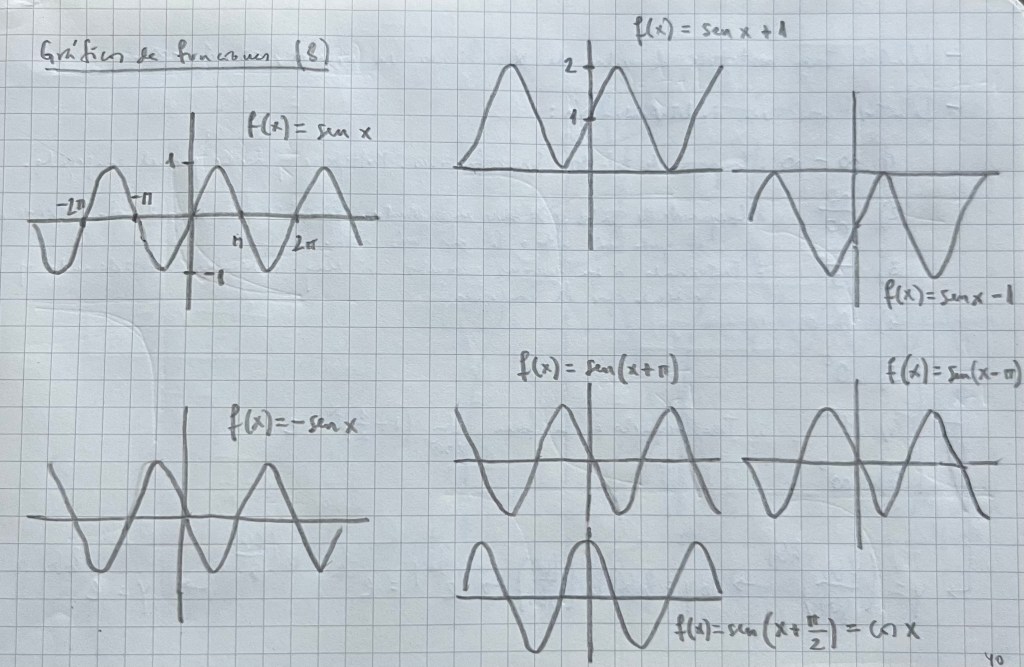
Funciones:

Una función es un tipo especial de relación. Es una relación que a todo elemento del conjunto A (denominado Dominio) se le asocia un único elemento del conjunto B (denominado Codominio o Recorrido).

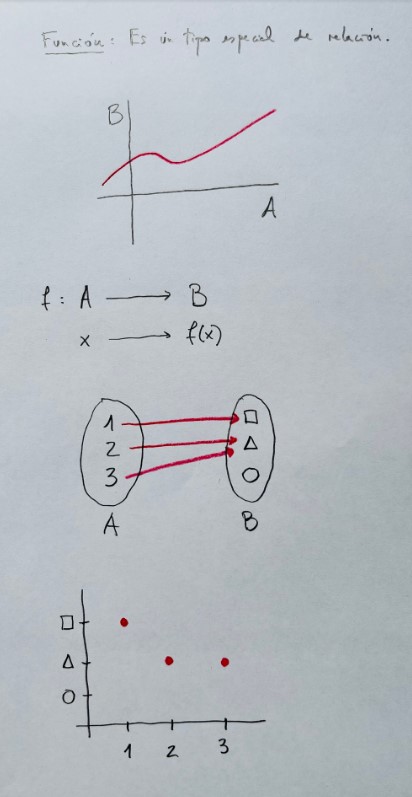
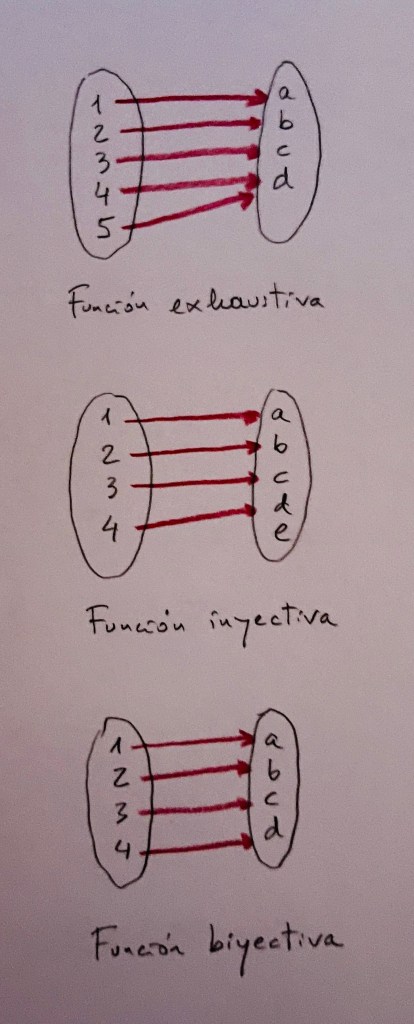
Antiimagen de un punto del codominio:

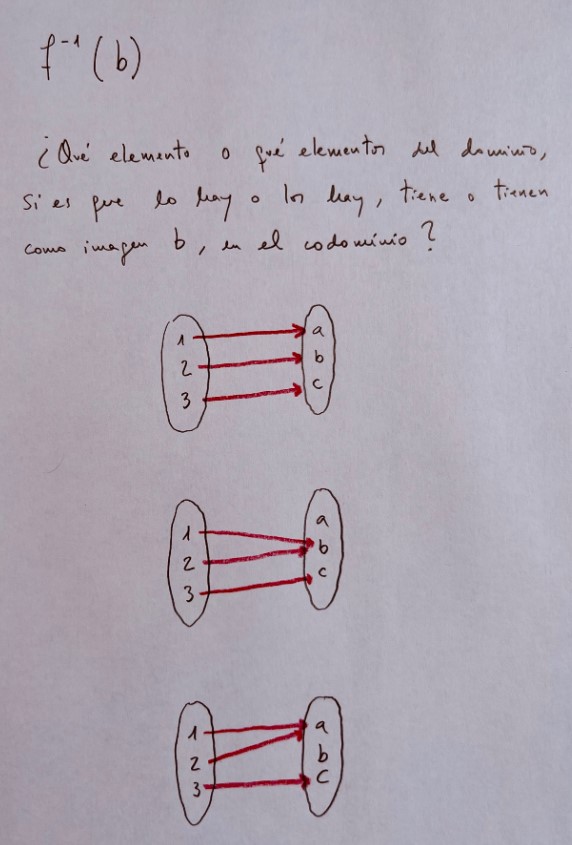
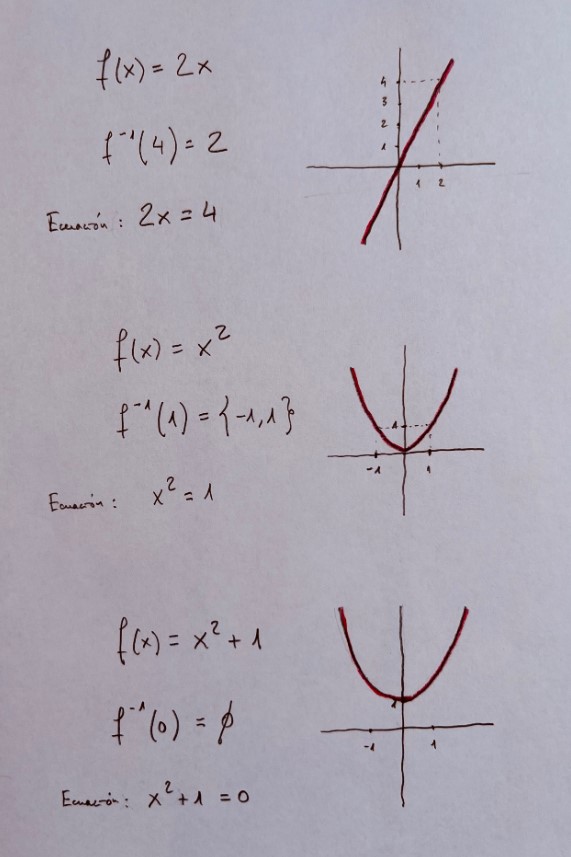
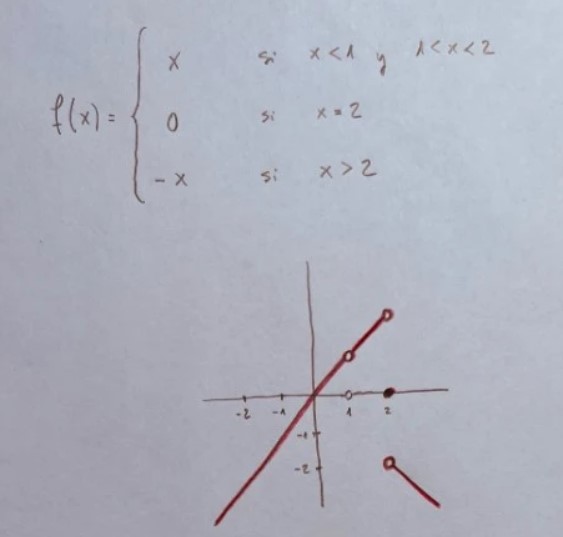
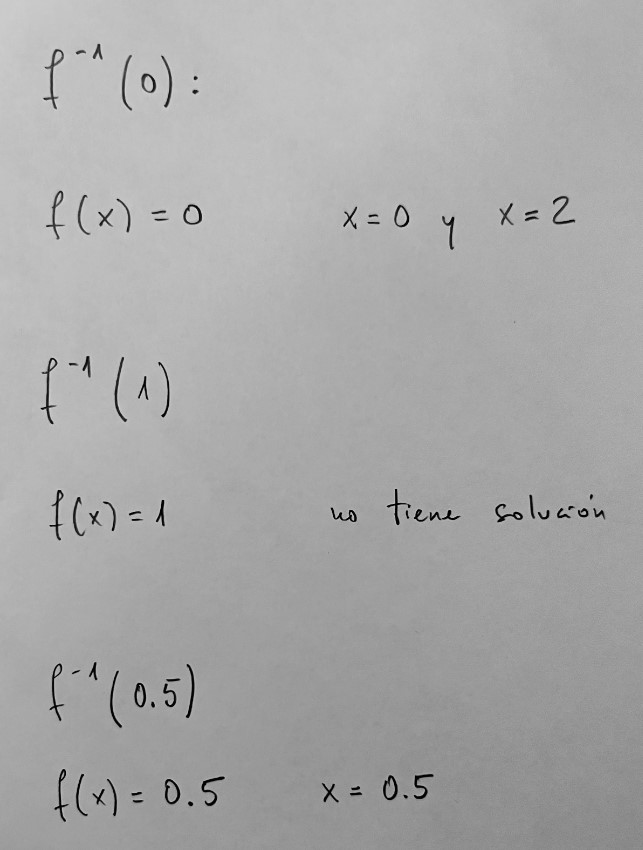
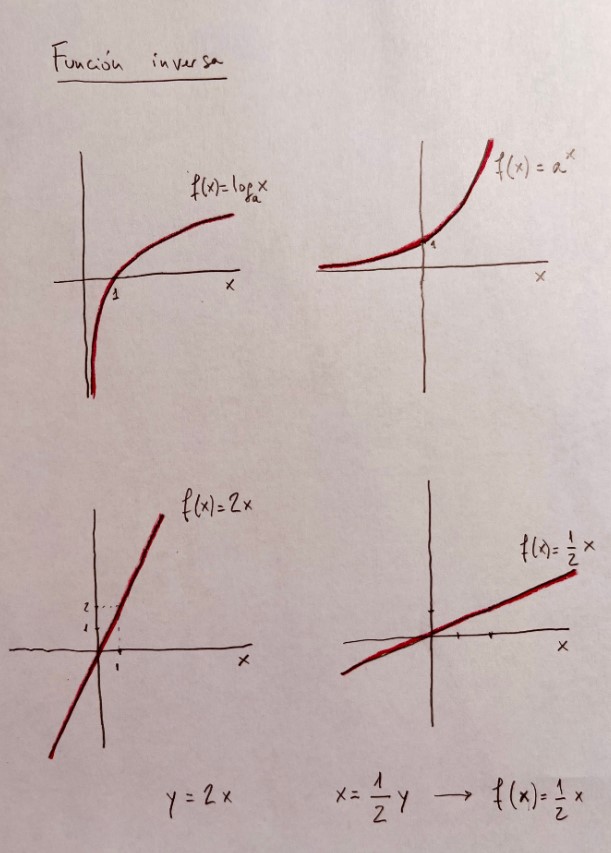
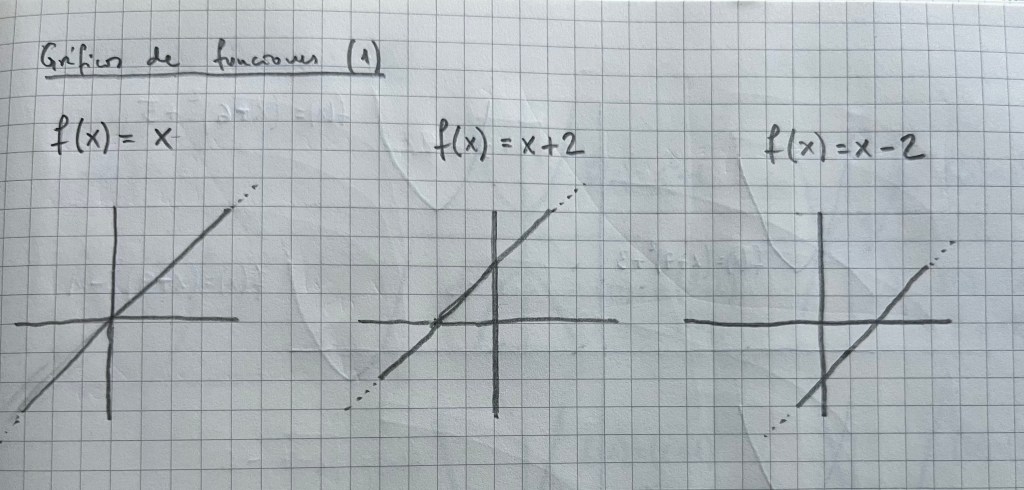
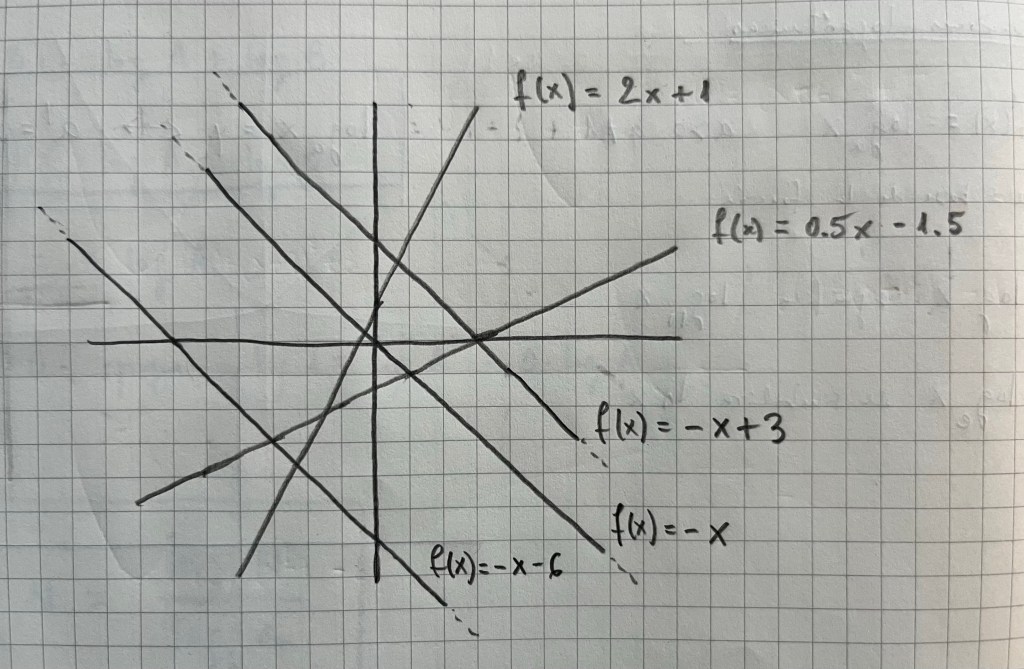
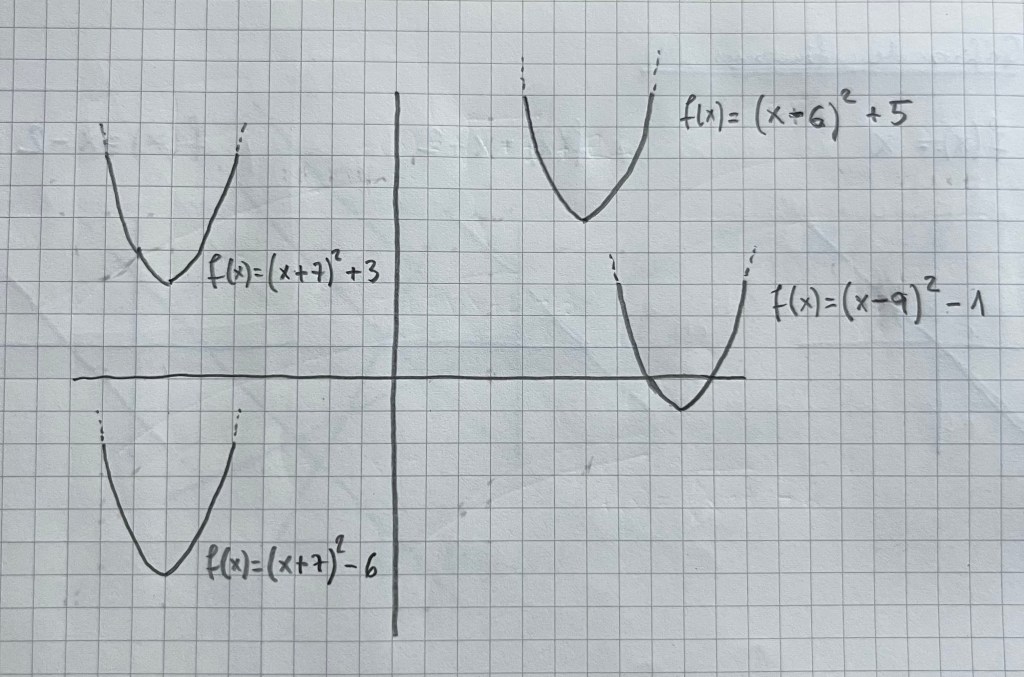
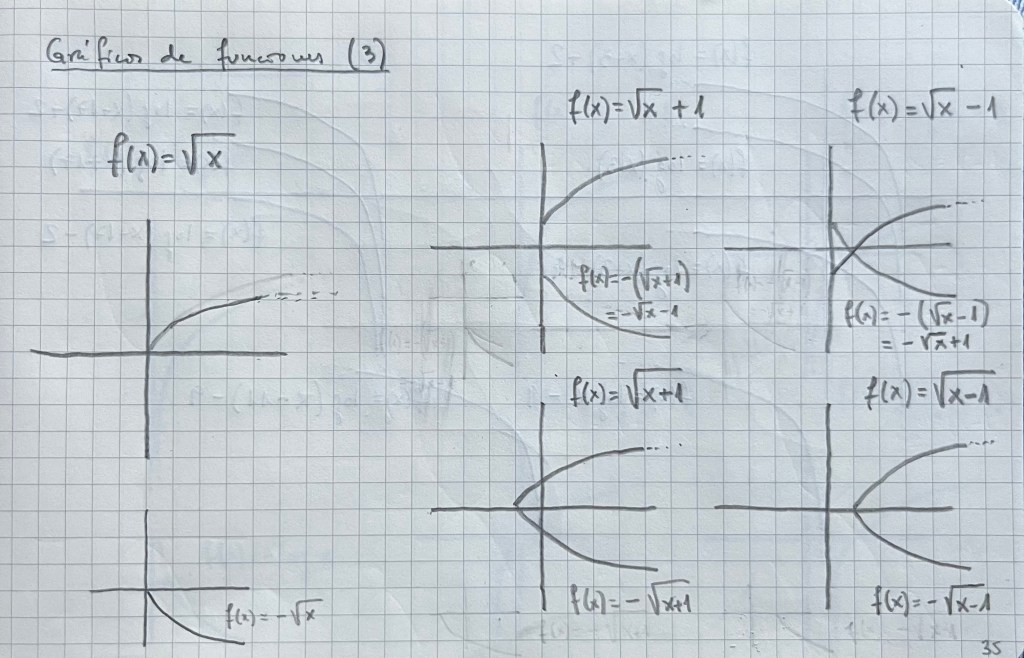
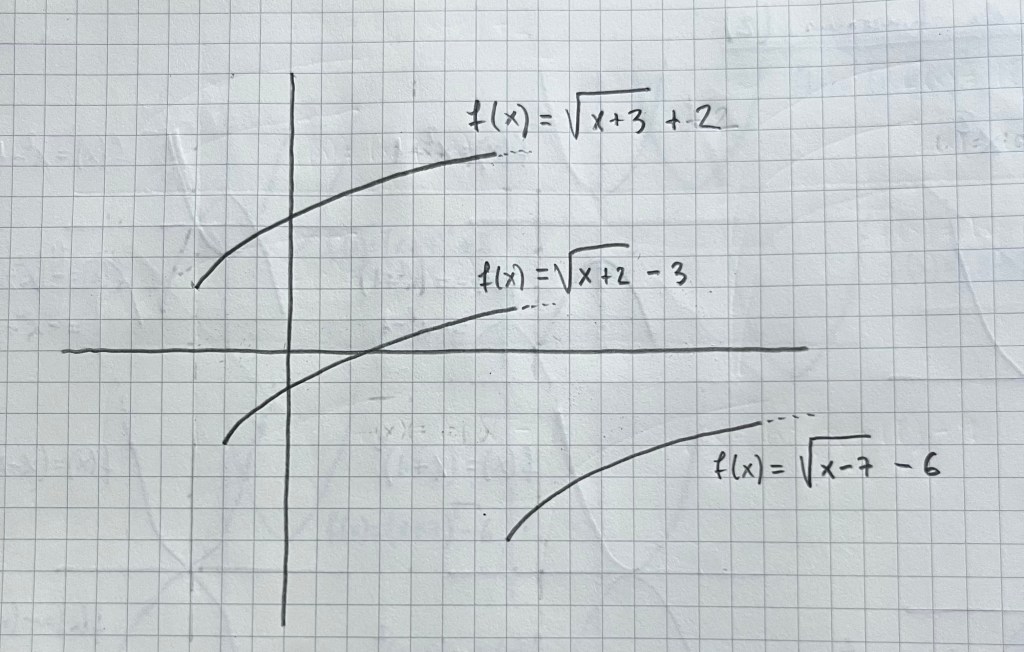
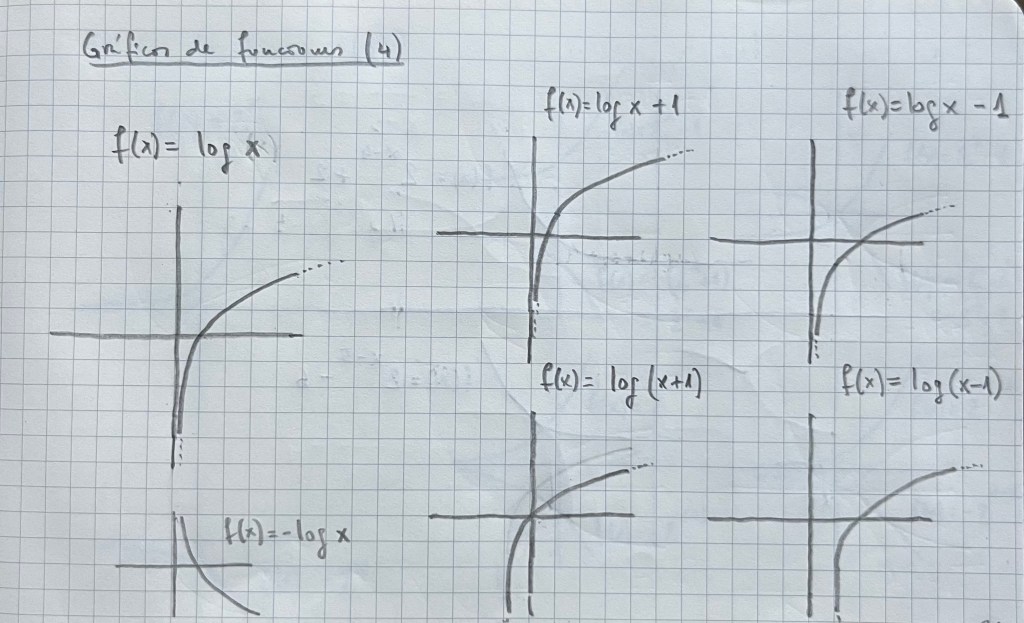
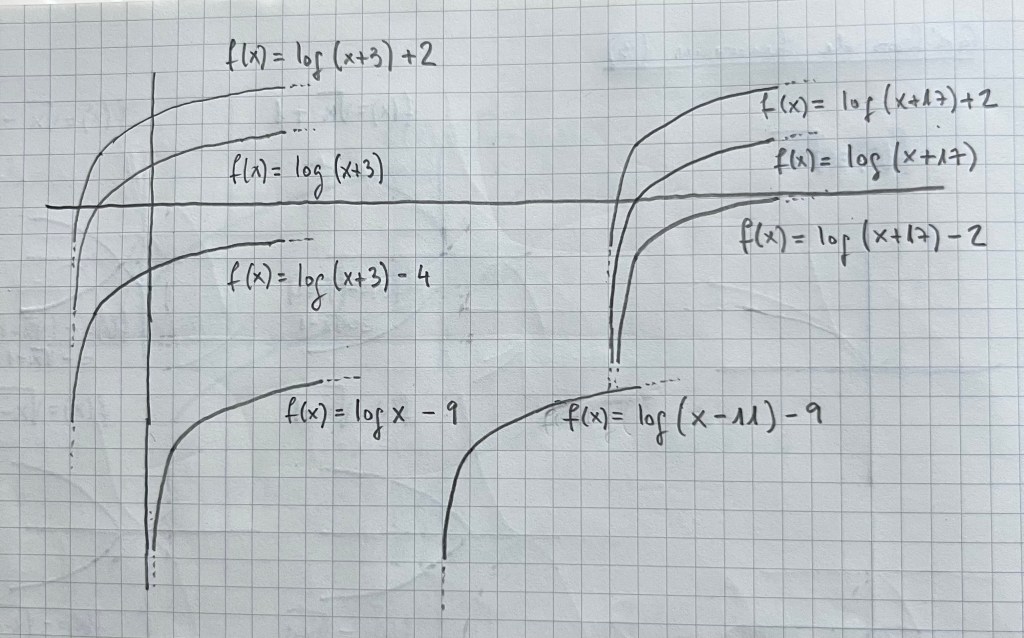
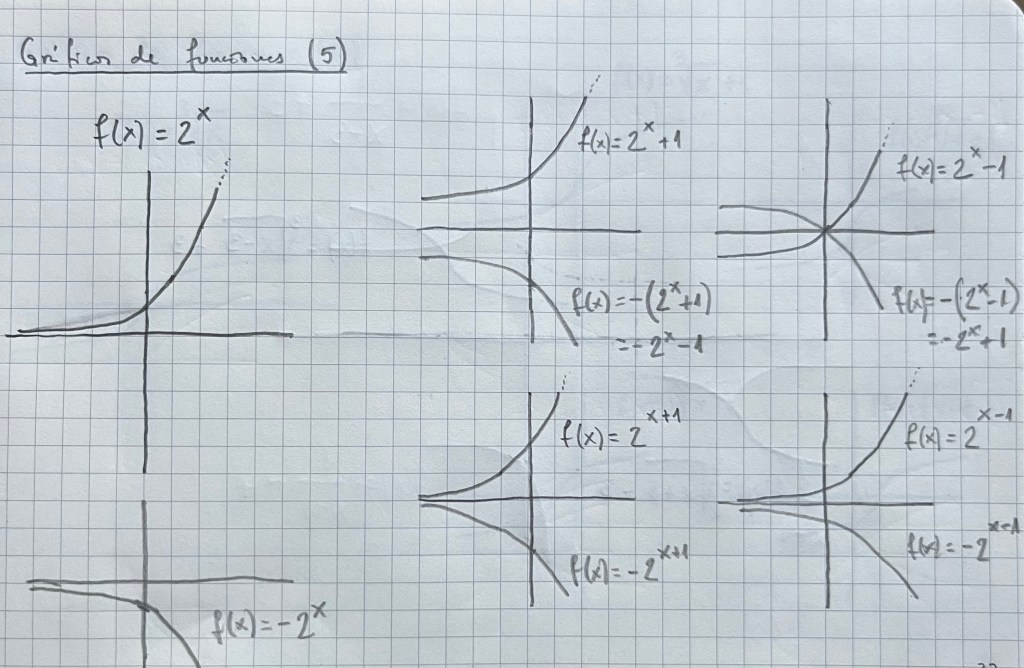
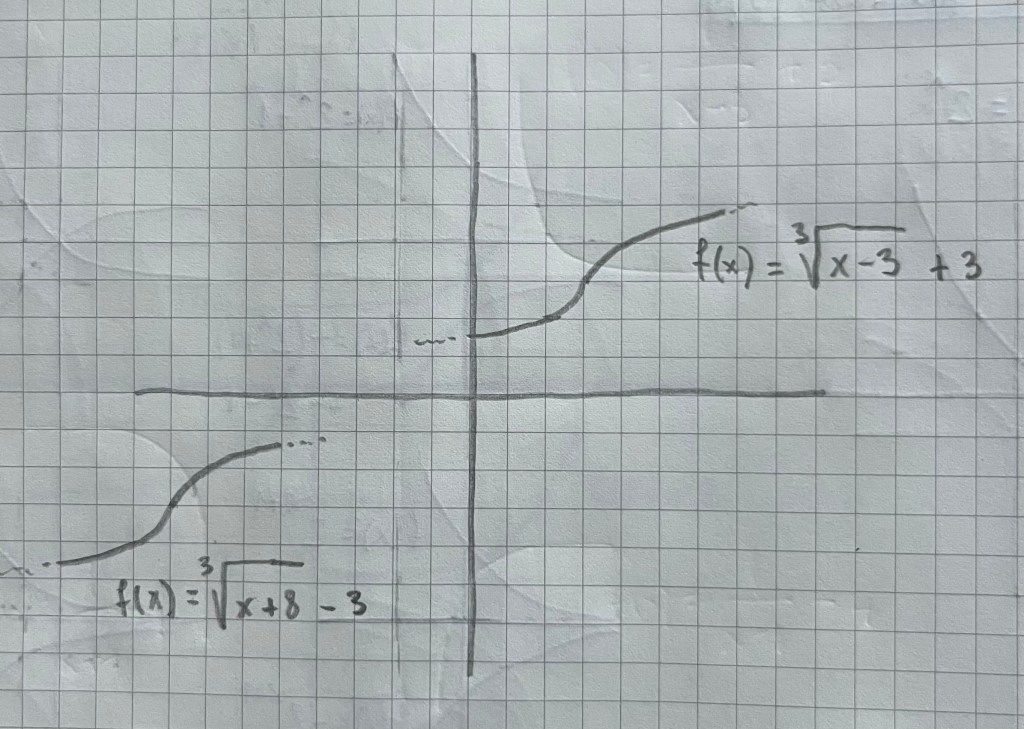
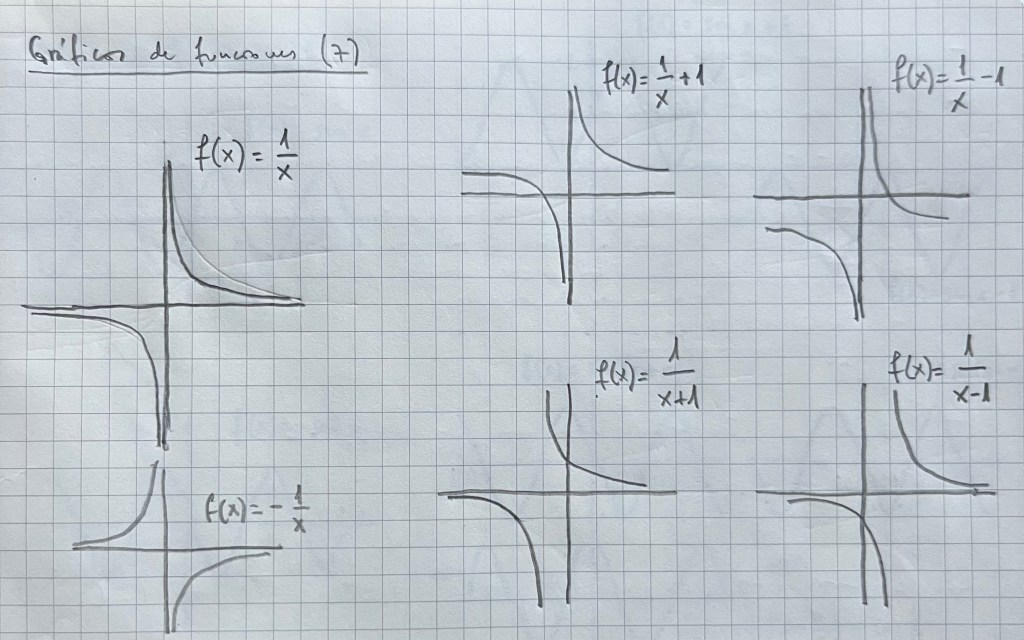
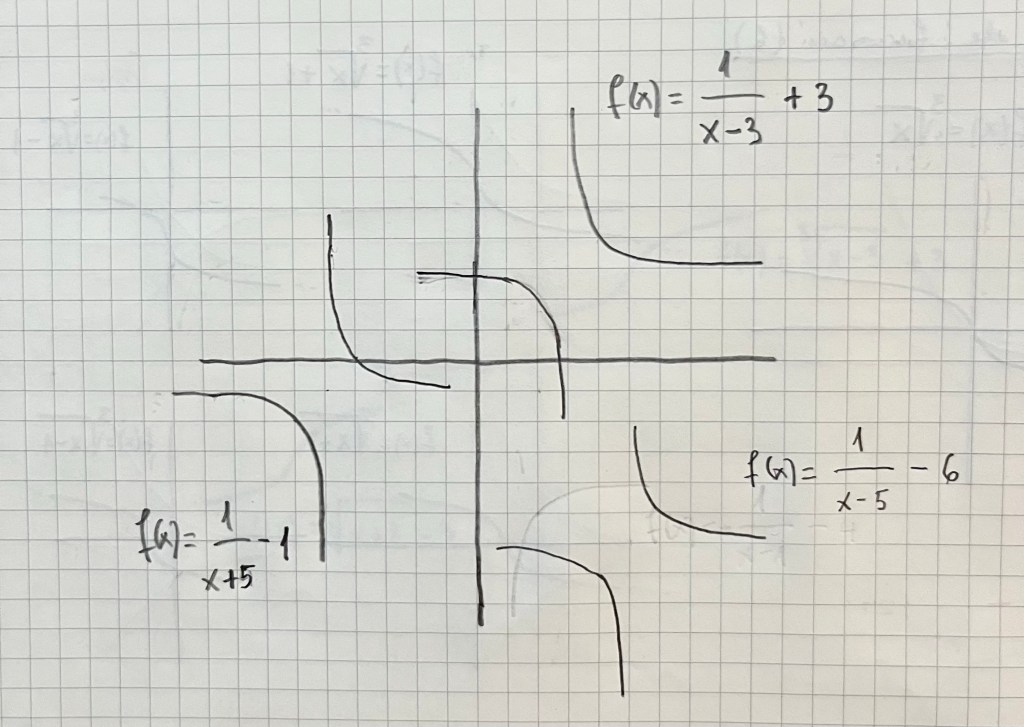
Es muy importante practicar con diferentes tipos de funciones vistas durante el bachillerato. La parametrización es una forma de ver diferentes funciones y su representación de una forma unitaria: