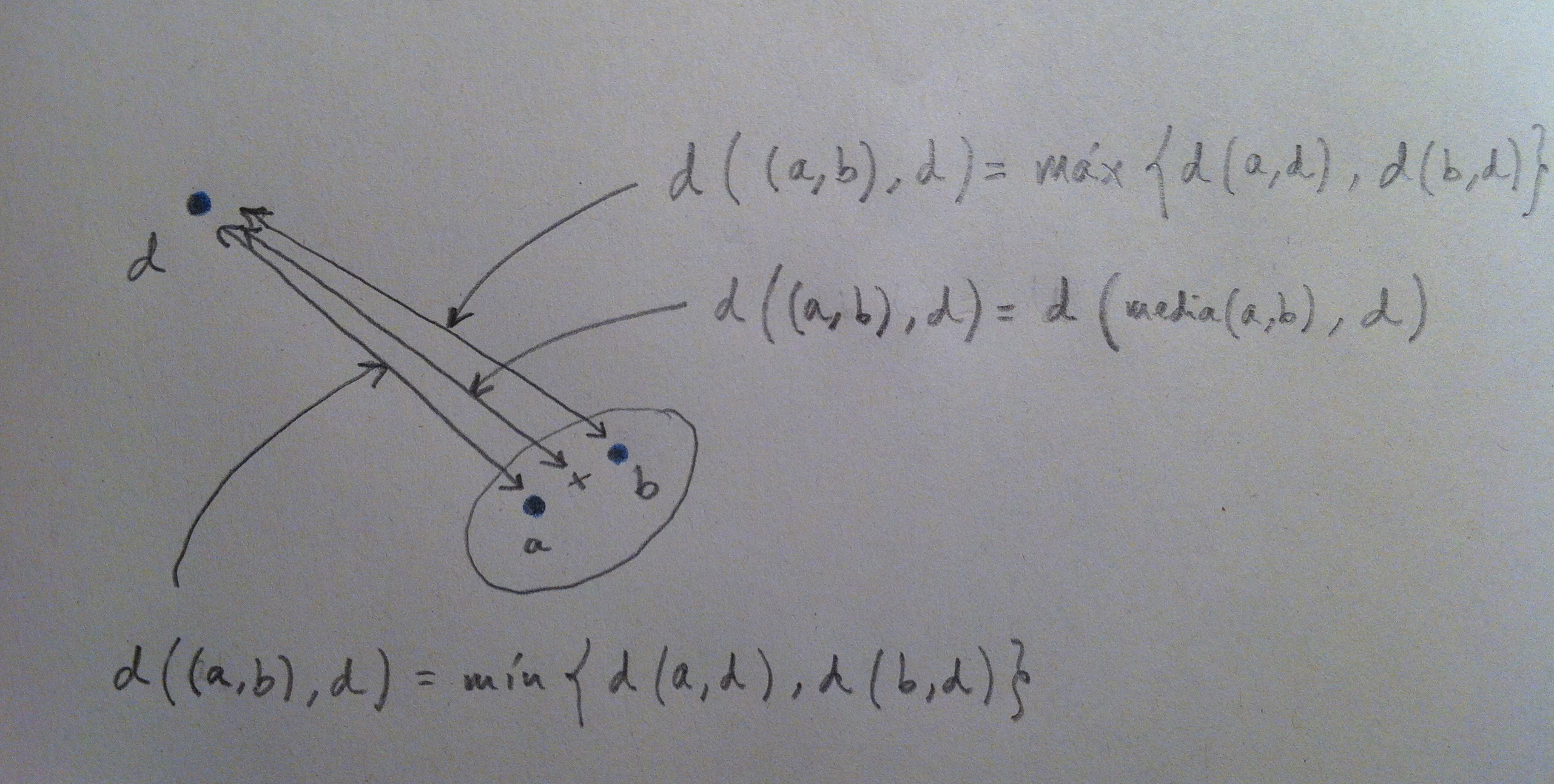
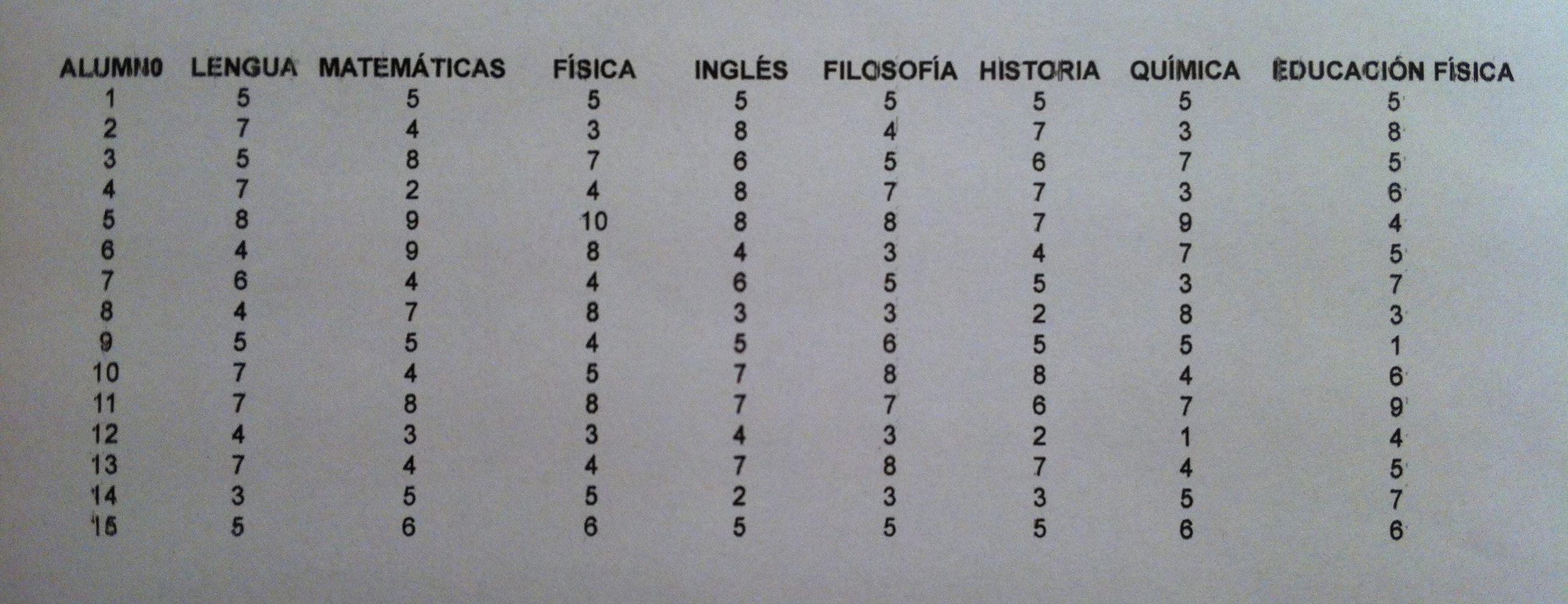
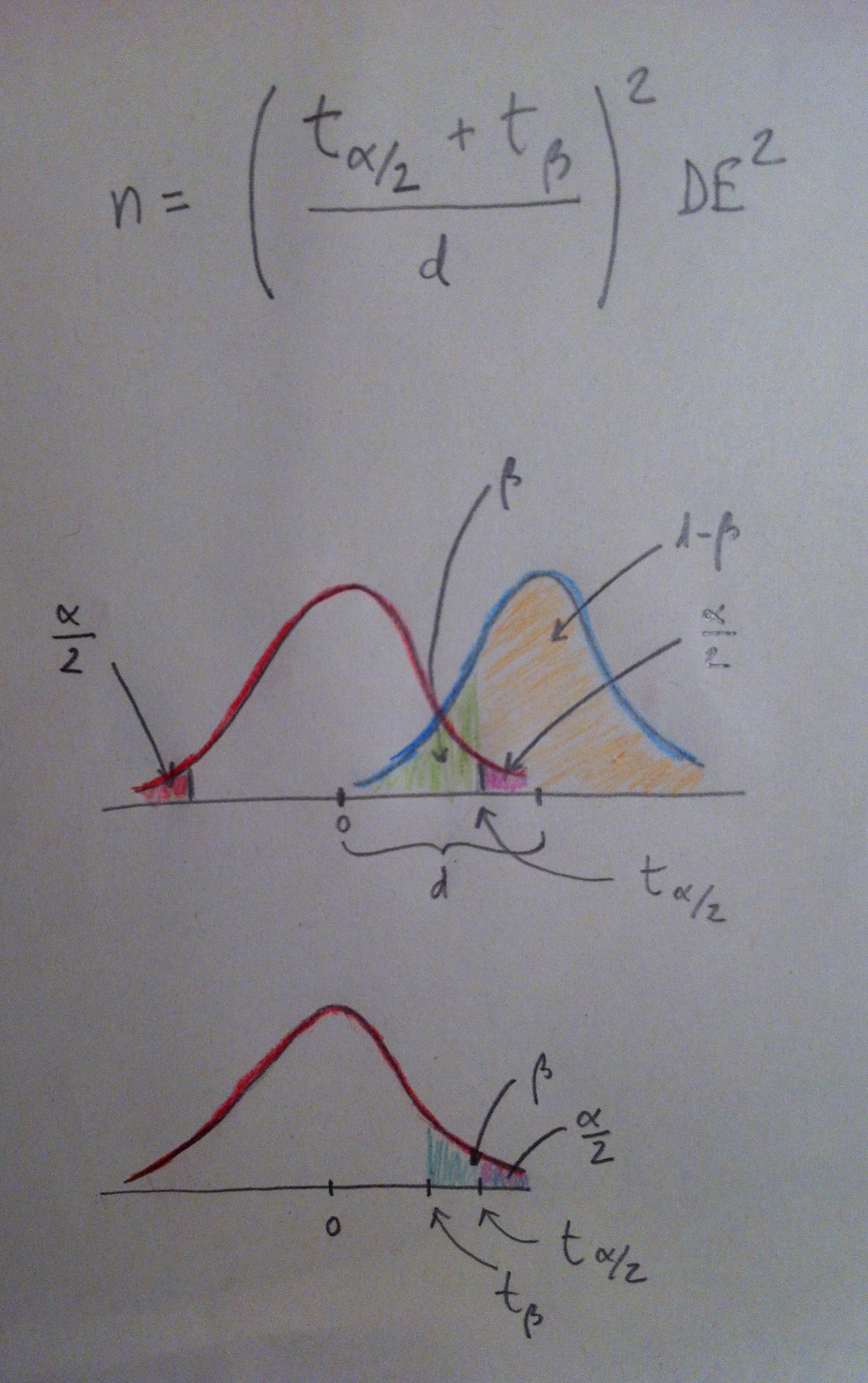
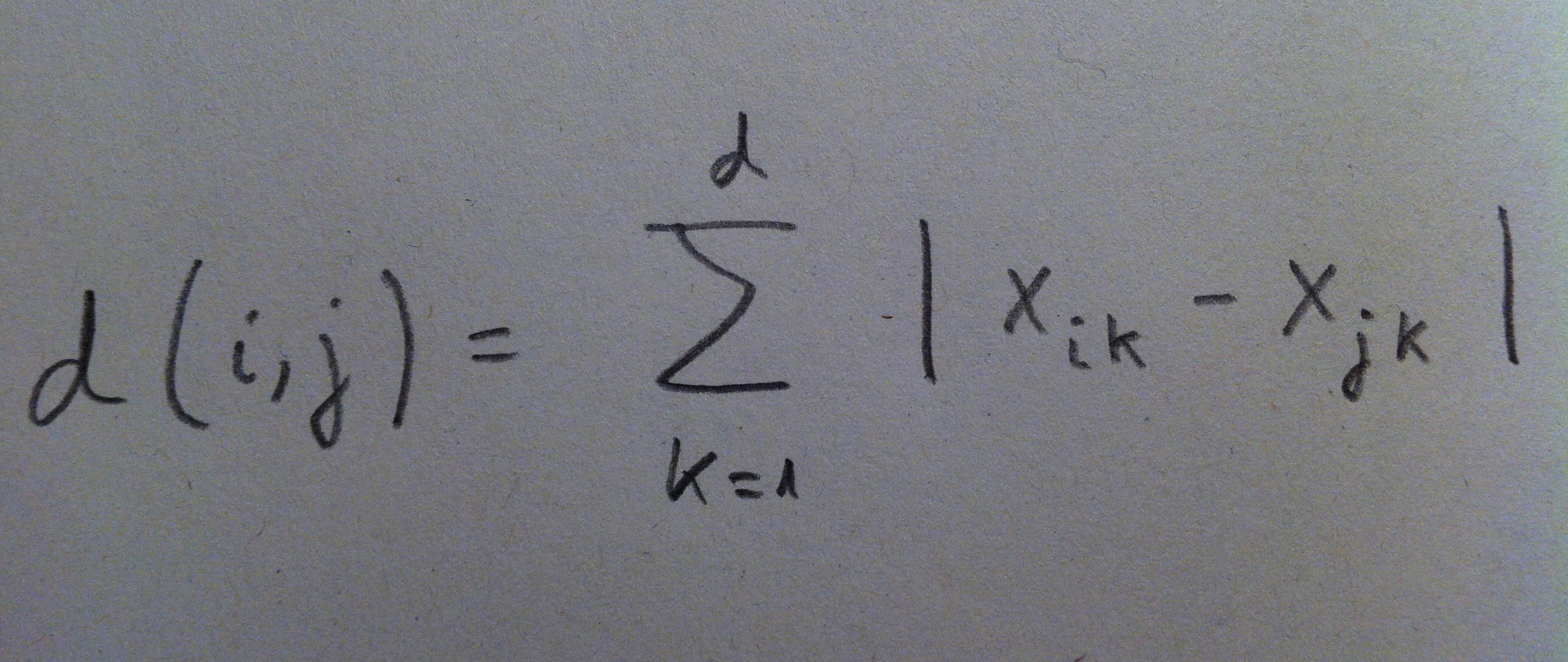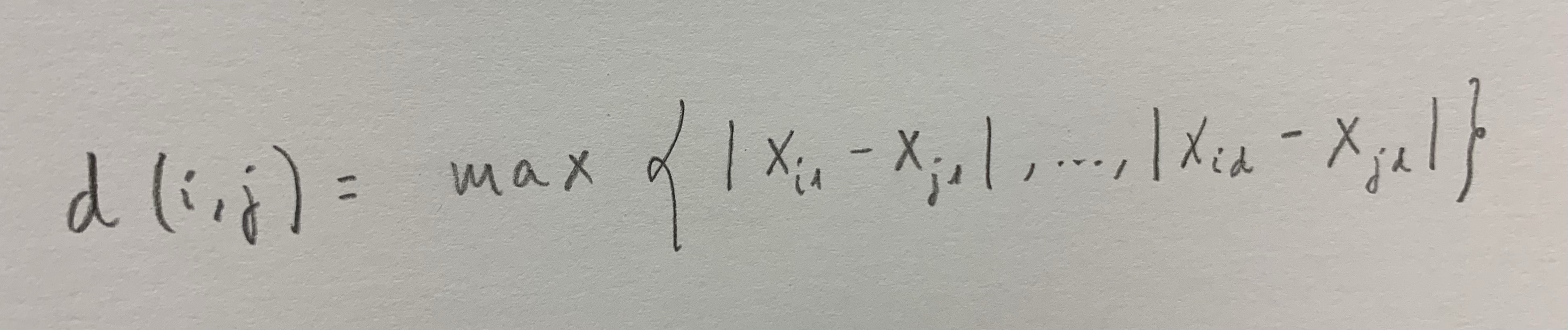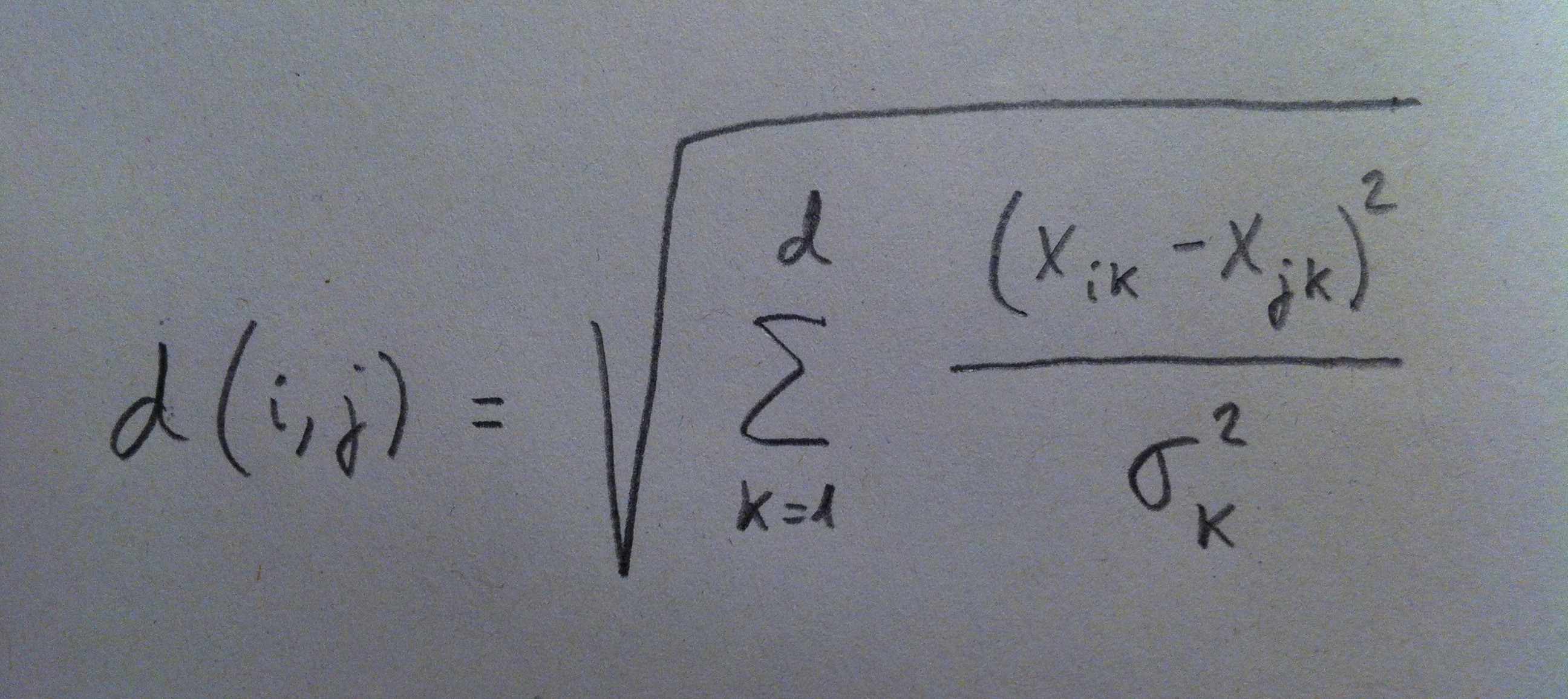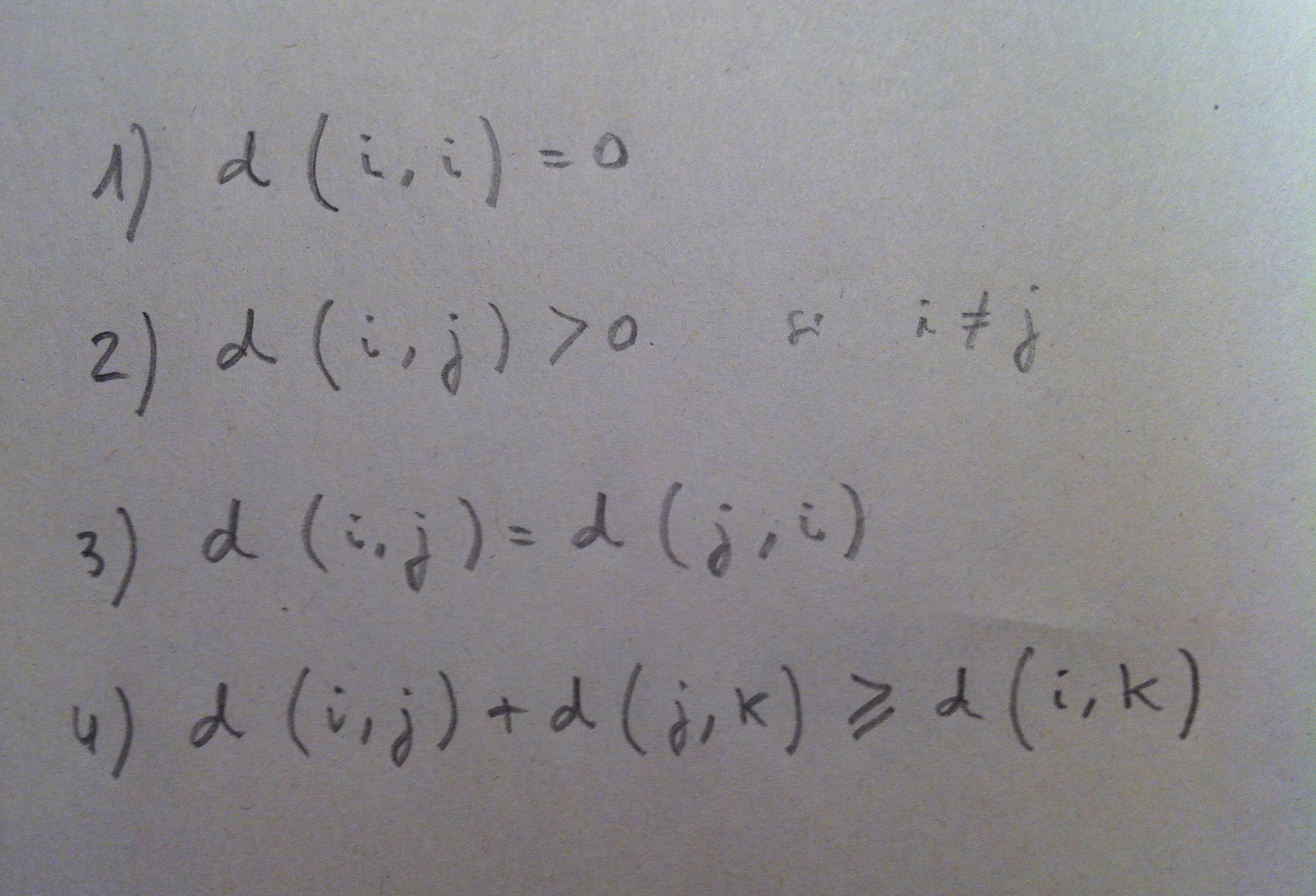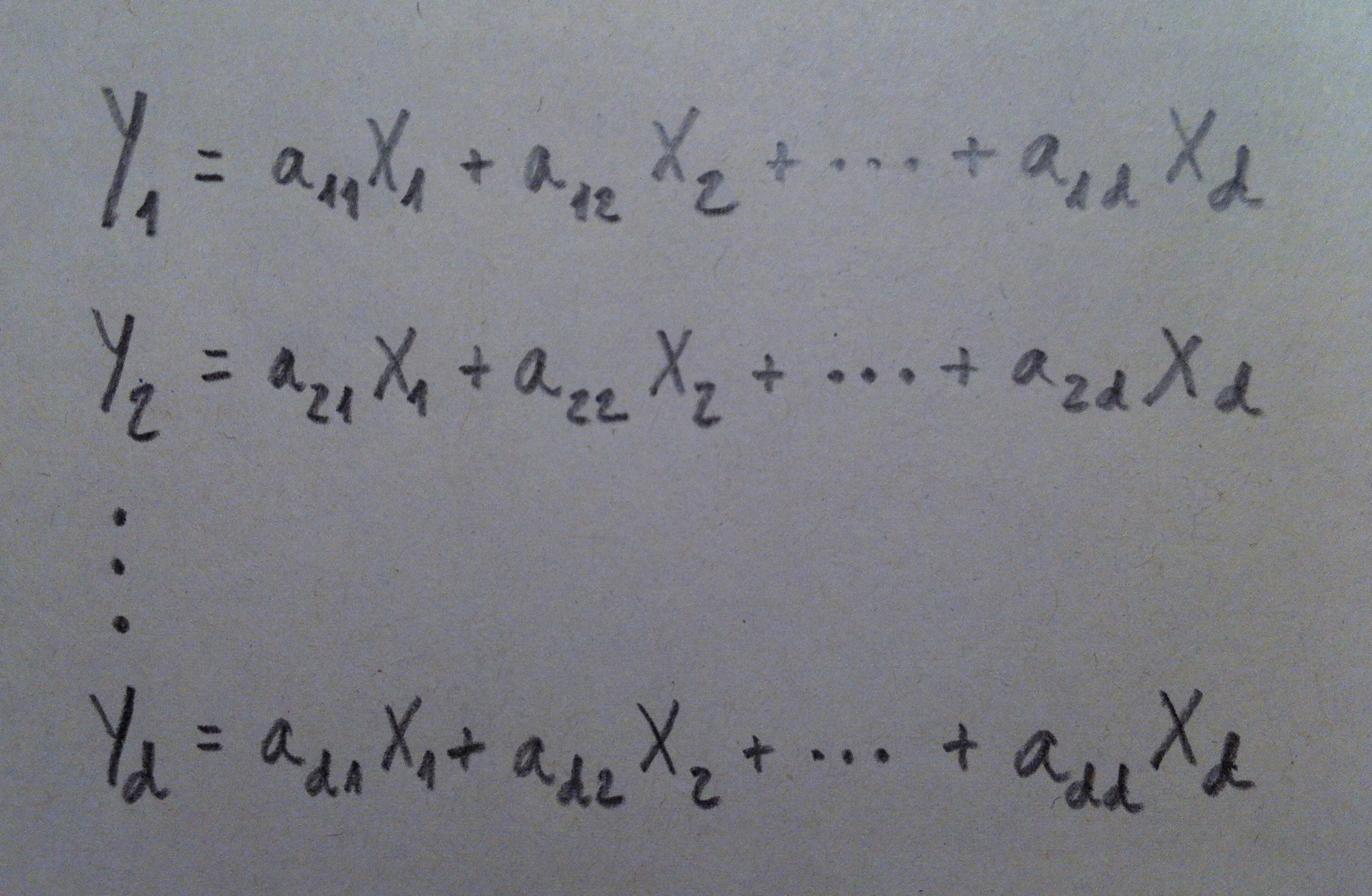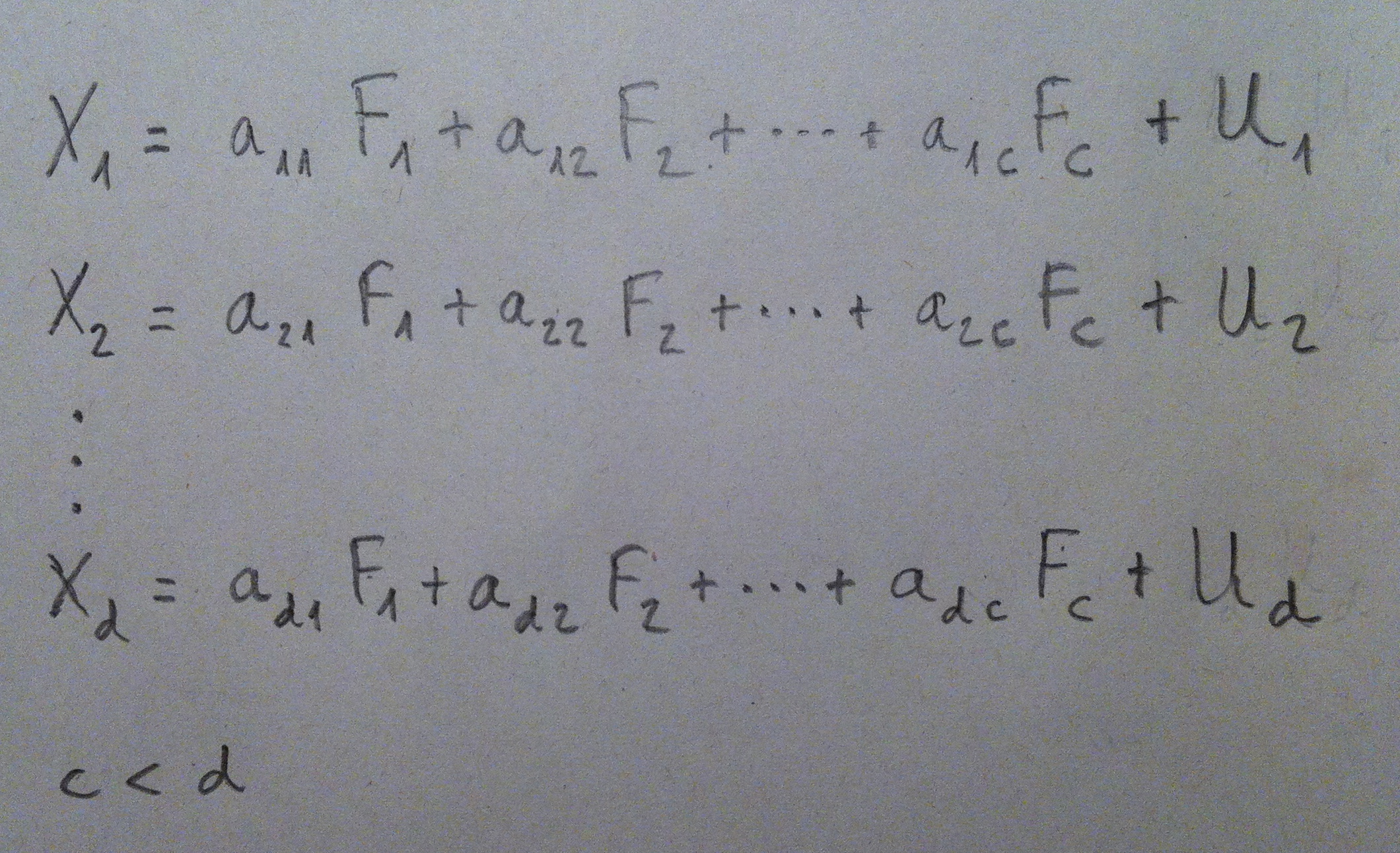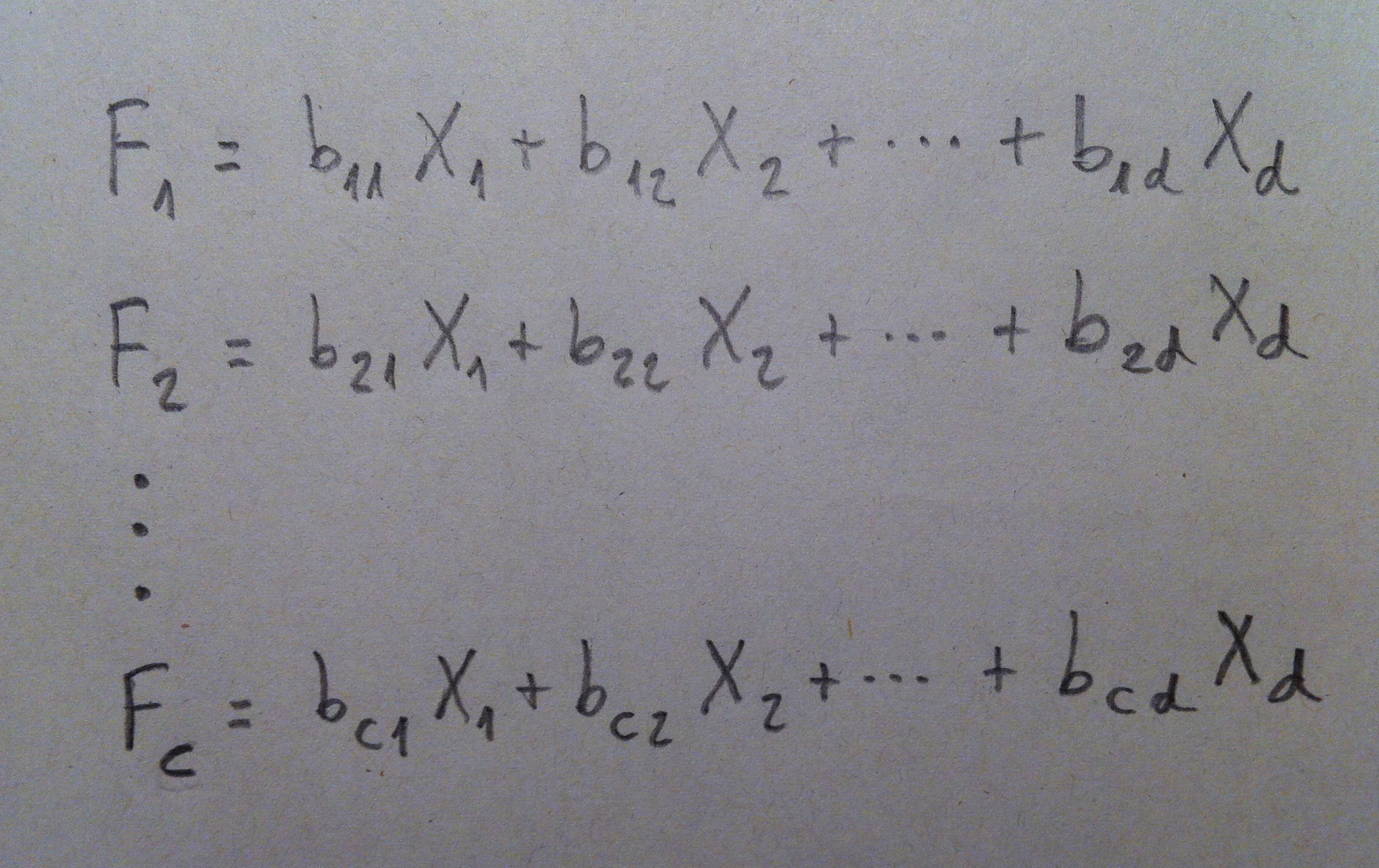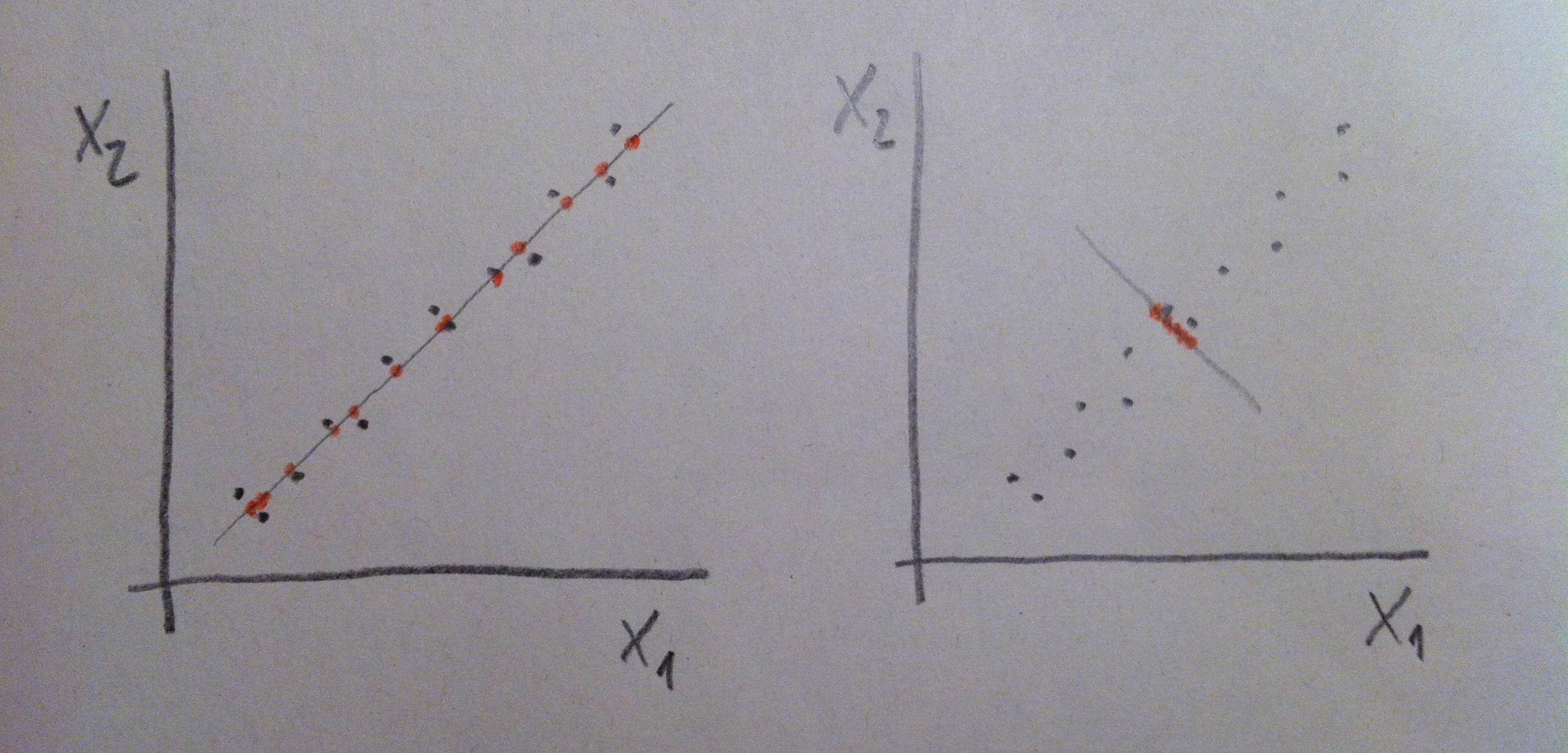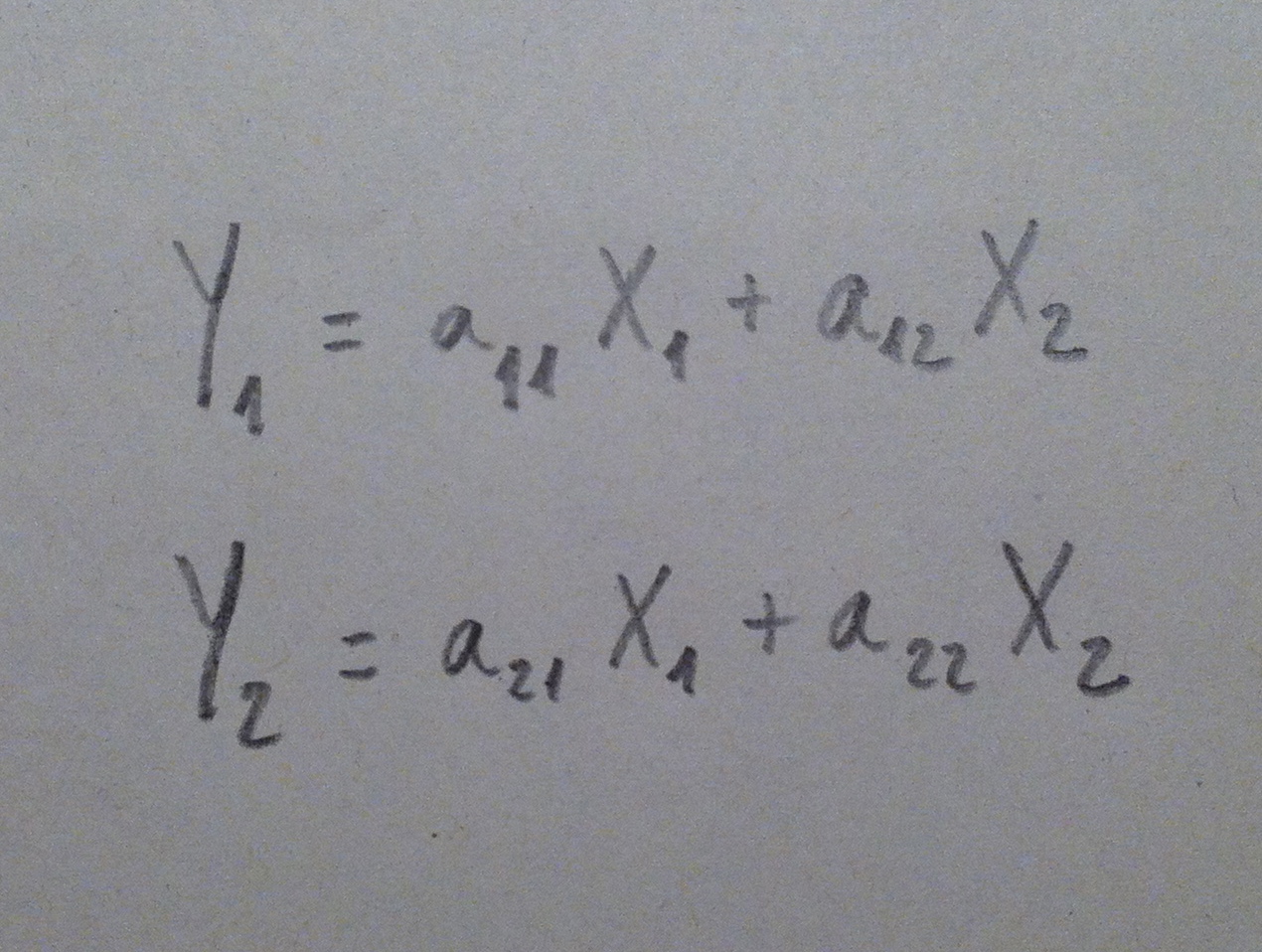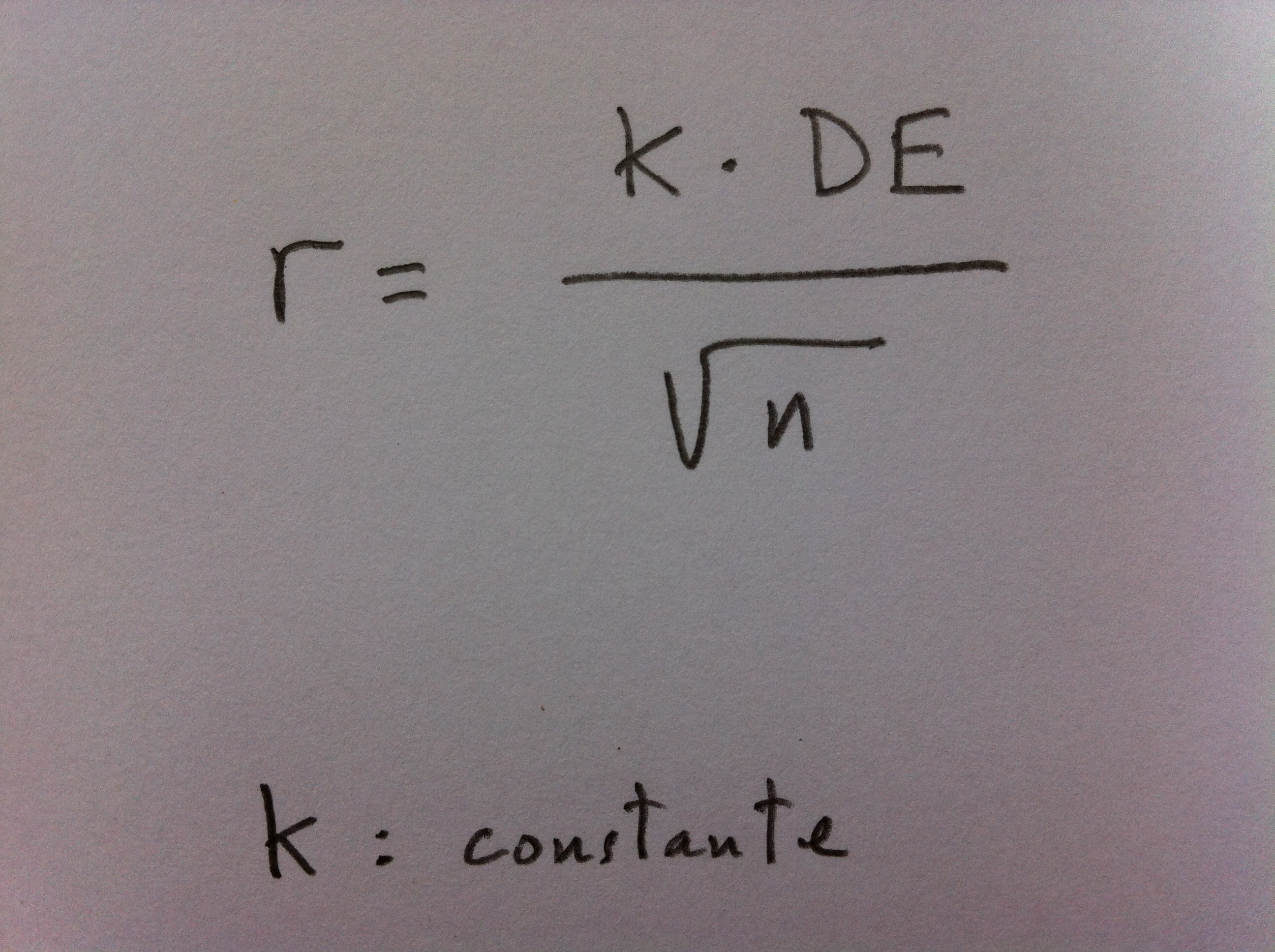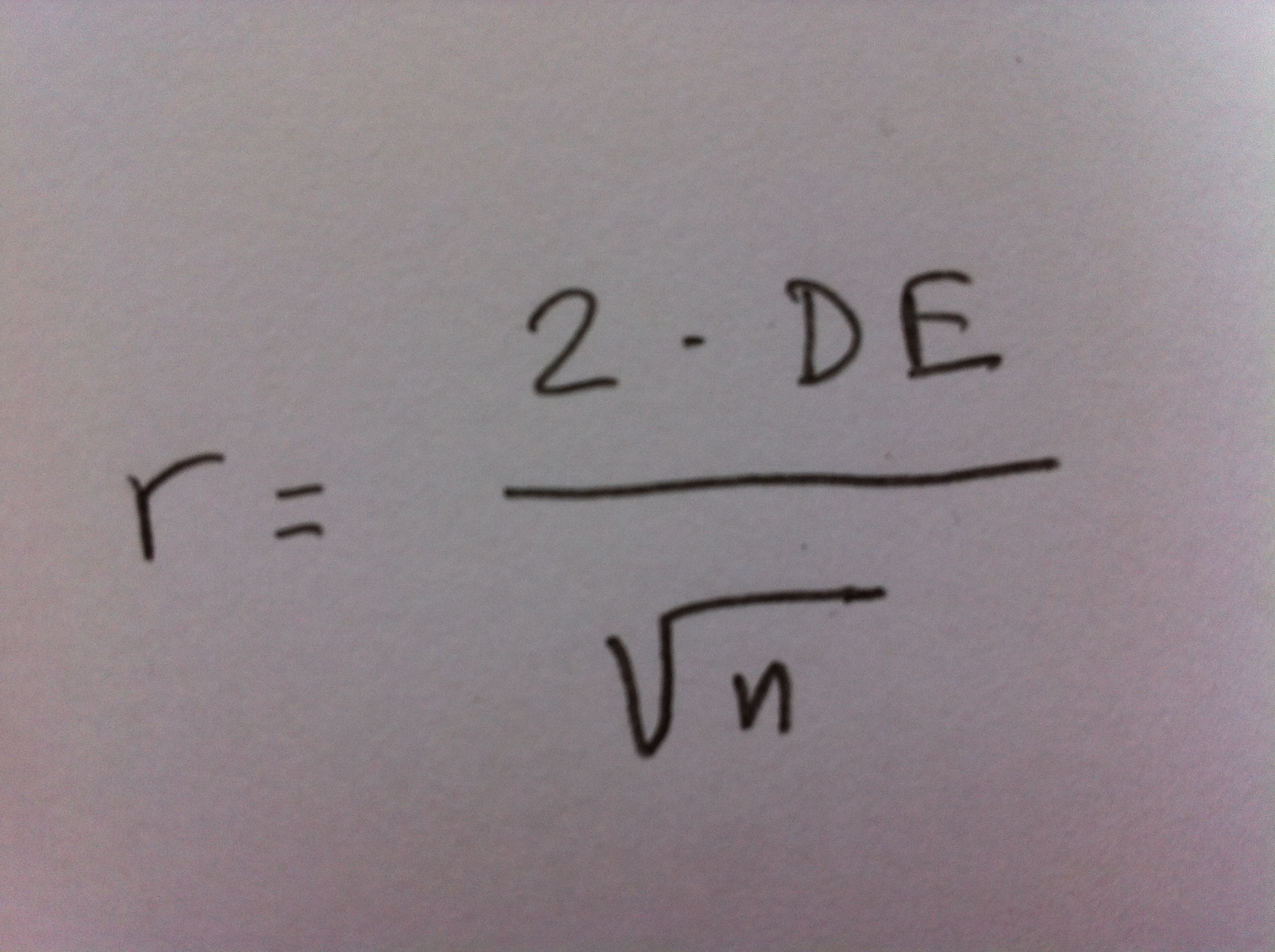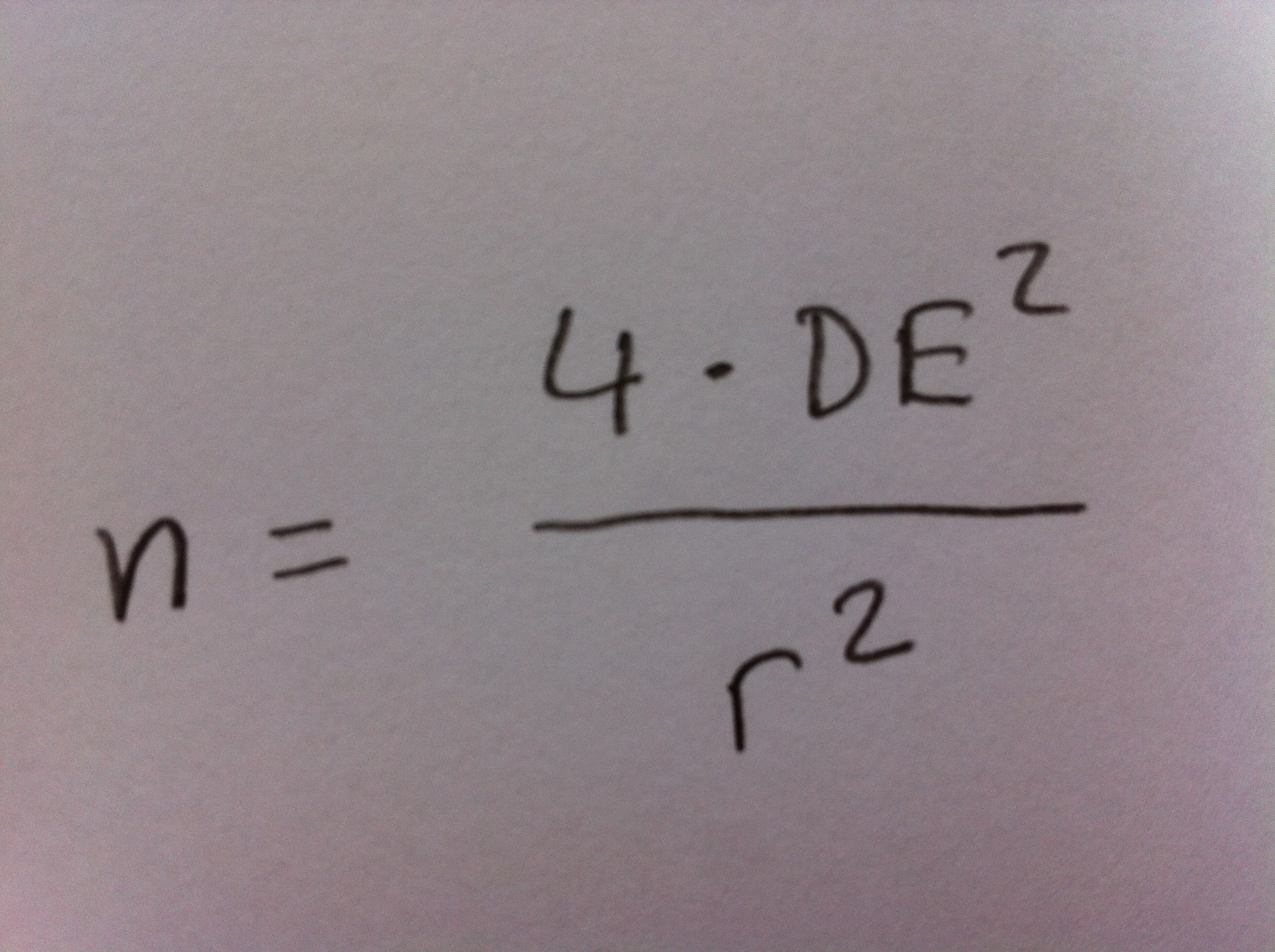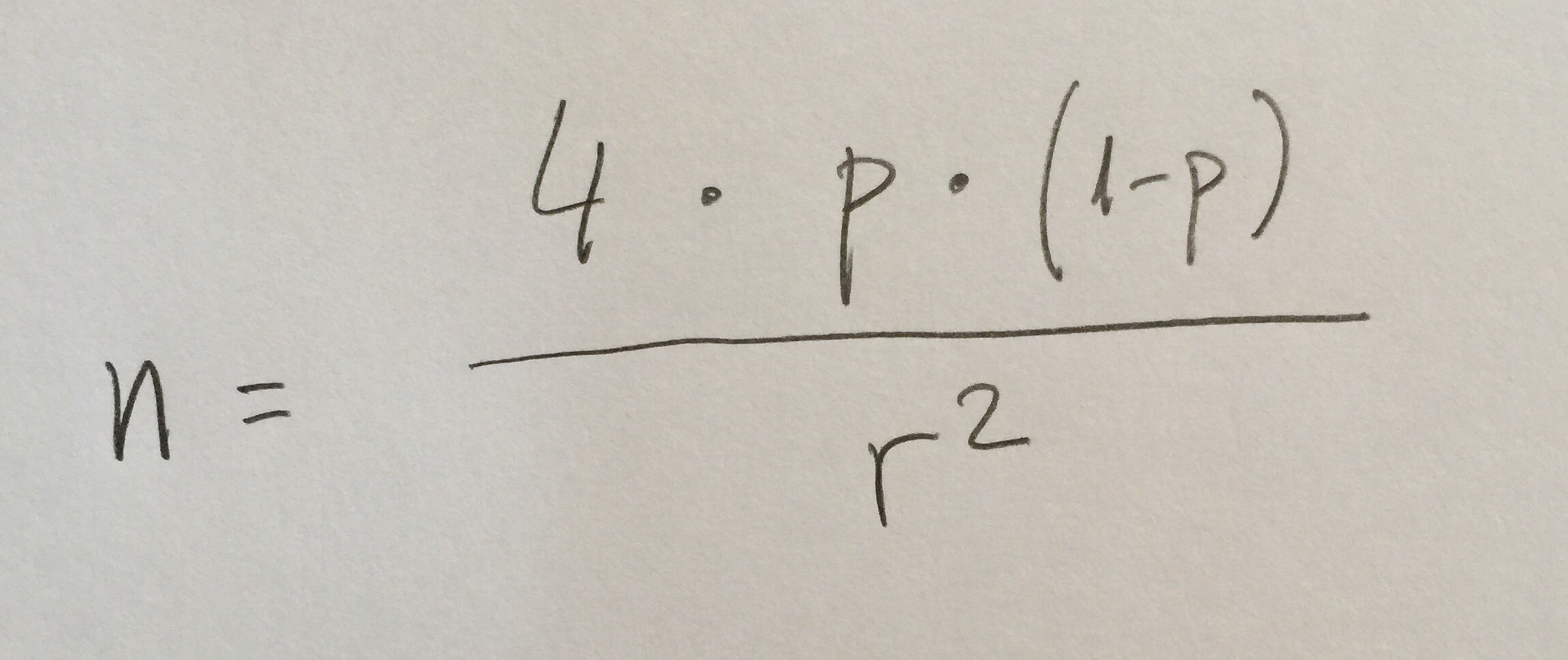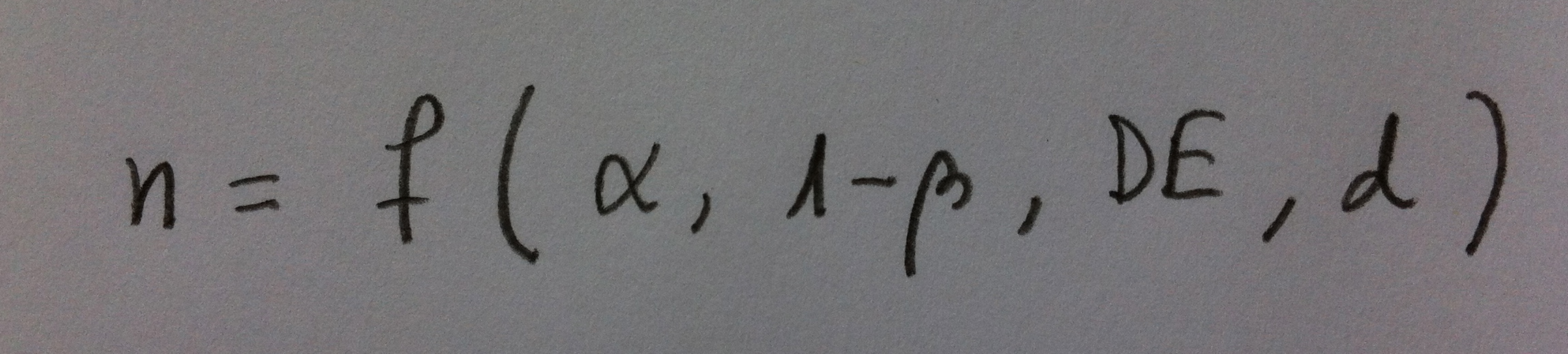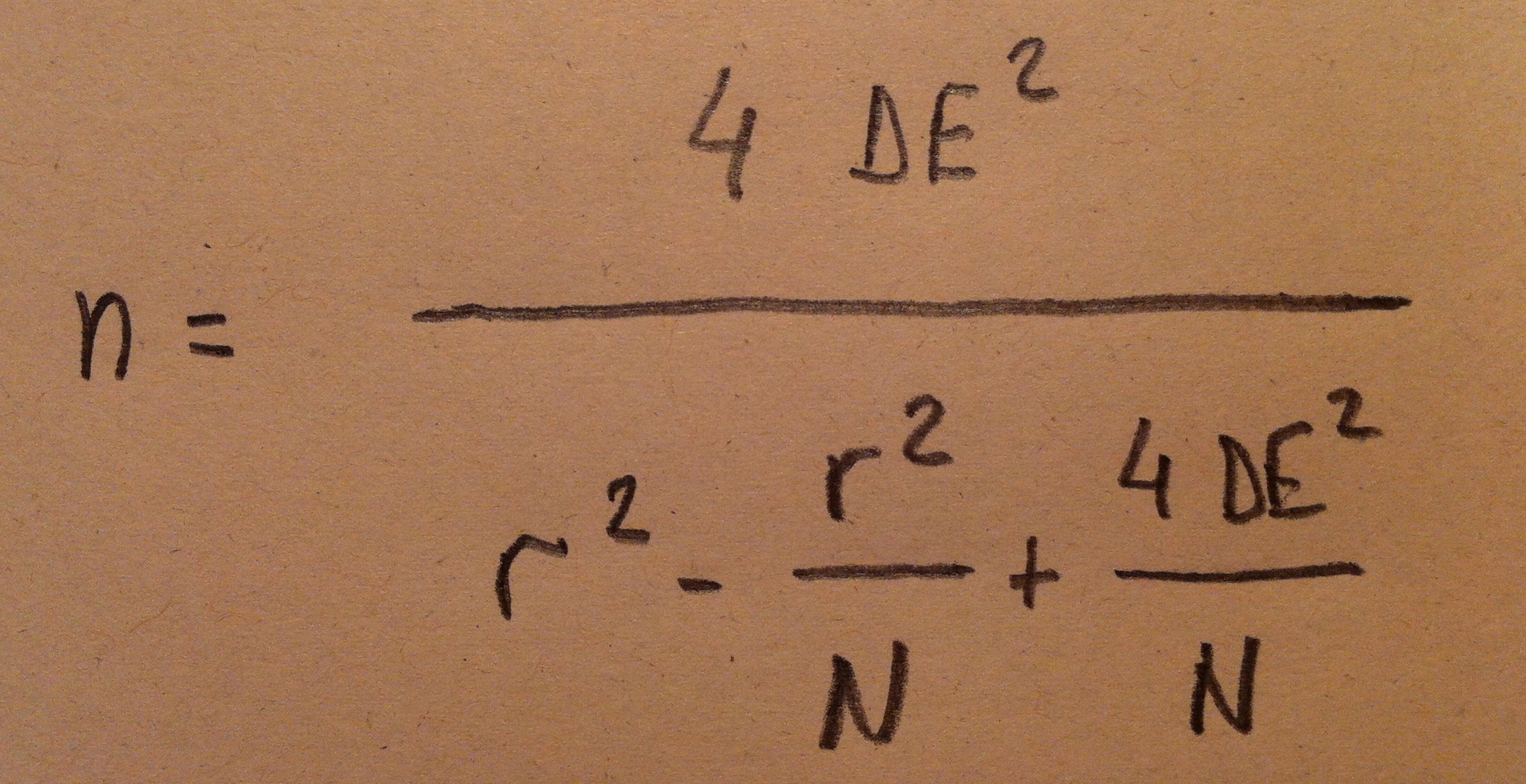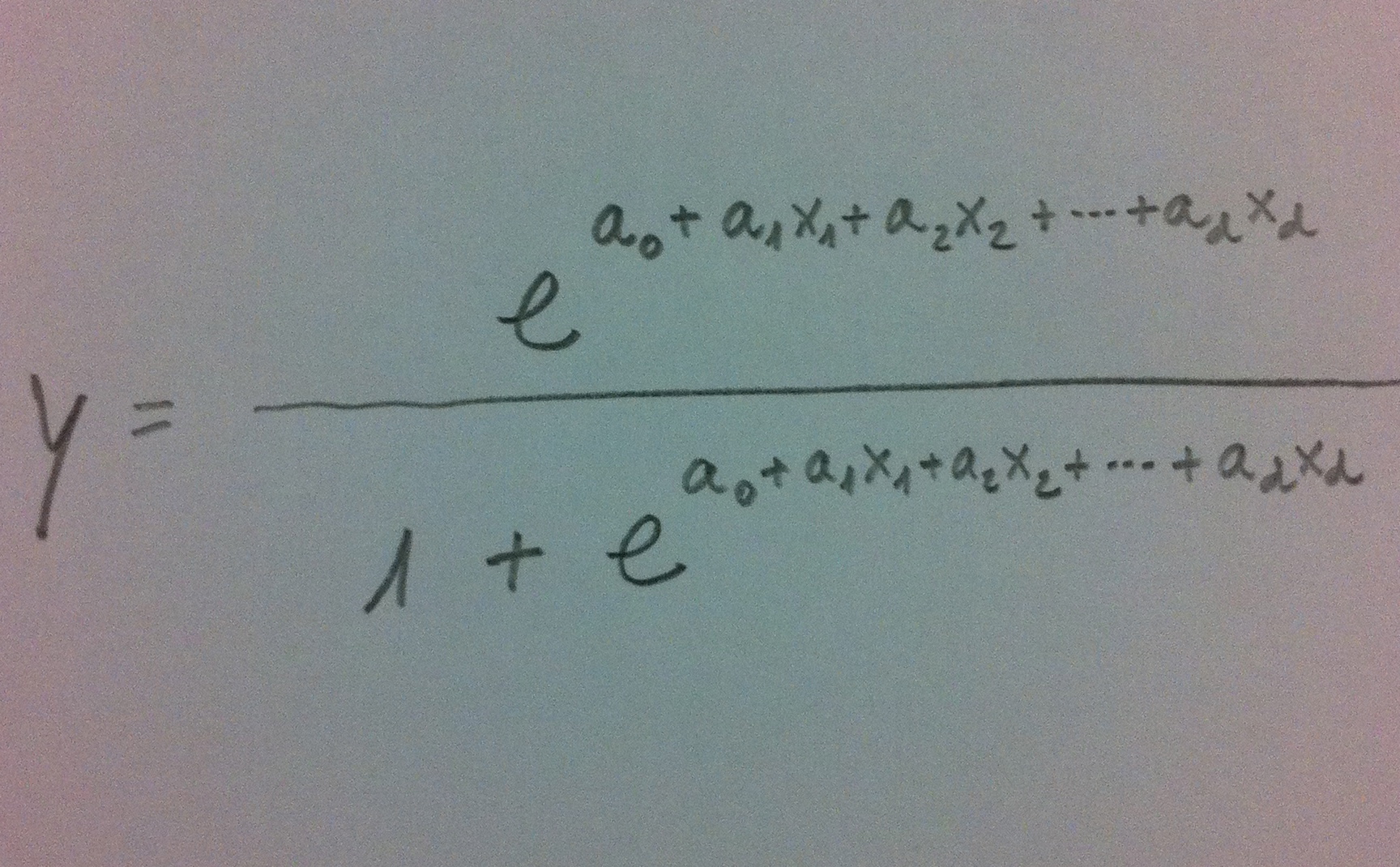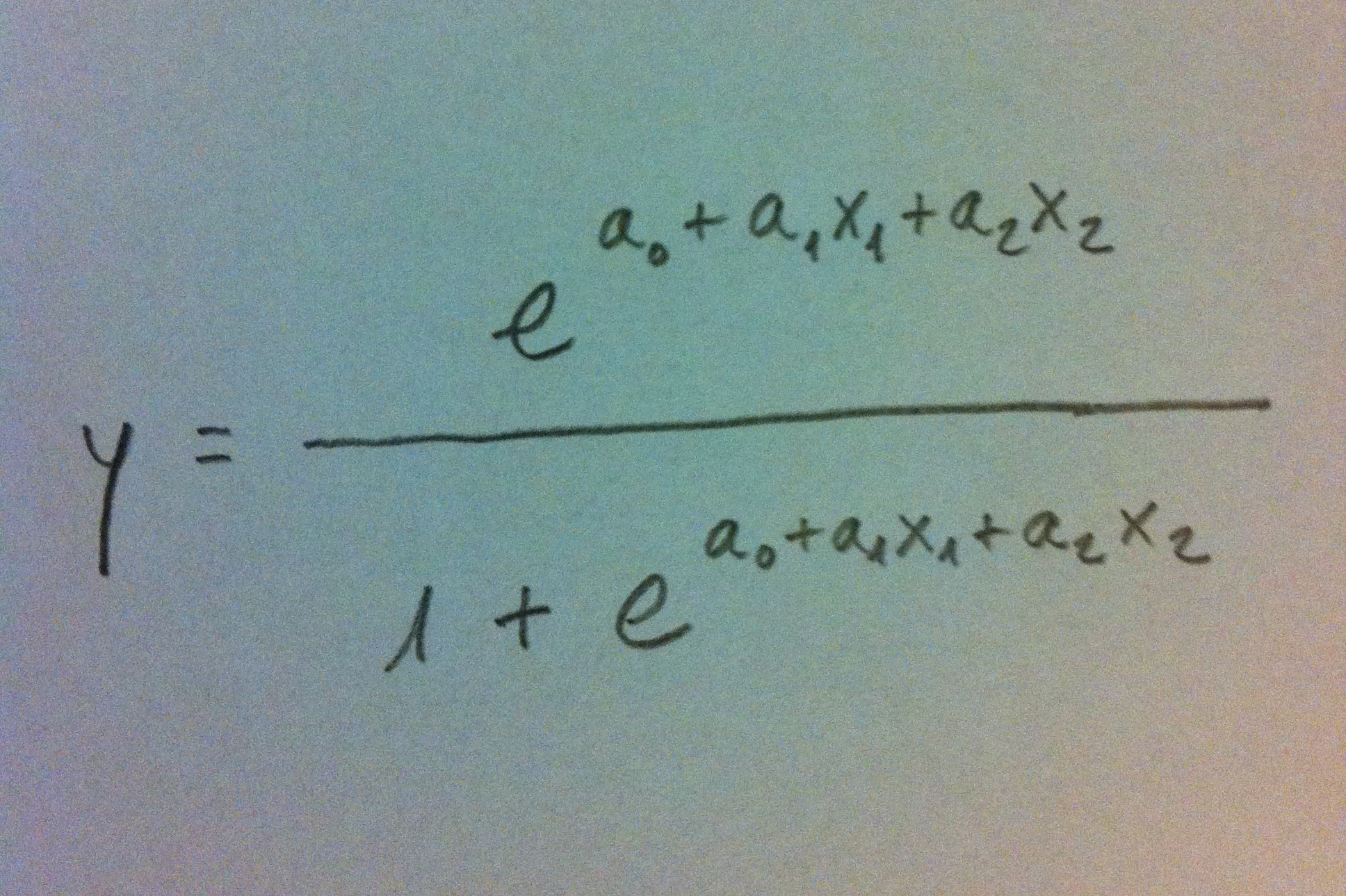1. El Análisis discriminante es una técnica inferencial. Es una técnica típicamente multivariante porque suele usarse en contextos donde tenemos varias variables, pero evidentemente puede aplicarse con pocas variables, incluso con una sola variable, pero no es lo habitual.

2. Una característica esencial de esta técnica es que tenemos previamente definidas dos o más poblaciones; o sea, tenemos dos o más muestras de esas poblaciones con una serie de individuos de cada una de ellas de los que tenemos medidas una serie de variables.

3. Su finalidad básica es preparar esa información, seleccionarla, trabajarla, con una finalidad clasificadora. Futuros individuos, a los que les podremos medir esas variables, deberemos clasificarlos como miembros de alguna de esas poblaciones.

4. Evidentemente partimos del supuesto de que esos nuevos individuos a clasificar pertenecen a una de esas poblaciones.

5. El Análisis discriminante tiene un nombre muy apropiado para lo que es su procedimiento. Porque lo que hace es iniciar, a partir de toda la información de que se dispone sobre las poblaciones y las variables, un proceso de discriminación, un proceso de separación lo mayor posible de esas poblaciones.

6. Por lo tanto, a partir de un conjunto de individuos que sabemos ciertamente a qué población pertenecen cada uno de ellos y a partir de los valores de todas las variables que disponemos mediante el Análisis discriminante tratamos de buscar qué combinaciones de esas variables nos permitirán discriminar lo más posible entre los grupos que tenemos.

7. Pongamos un ejemplo previo sencillo que puede ayudarnos a clarificar el camino de la explicación de esta técnica: Supongamos que queremos encontrar variables que nos permitan clasificar a una persona entre hombre o mujer teniendo únicamente la información de la medida de esa variable.

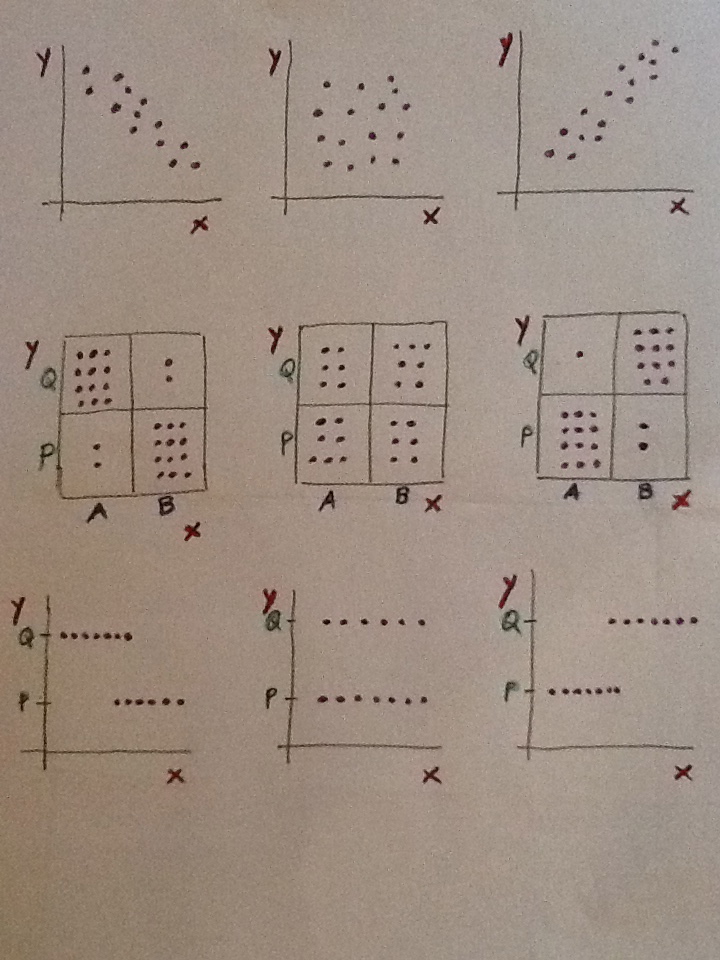
8. La variable edad no discrimina entre hombres y mujeres, no separa bien esos dos grupos. La variable altura ya discrimina más. La variable pie que calza discrimina más aún. Veámoslo en unos datos posibles: En rojo tendríamos una muestra de mujeres y en azul una de hombres:

9. Elegir la edad para pronosticar el sexo nos llevaría a mucho error. La mitad de las veces nos equivocaríamos. Elegiendo la altura ya cometeríamos menos errores porque las poblaciones están más discriminadas, más separadas, respecto a esta variable. Eligiendo el pie que calza cometeríamos menos errores aún porque de las tres variable es la que discrimina mejor, es la que separa mejor a los dos grupos, como puede apreciarse en este gráfico. Esto es así en la realidad: en mujeres y hombres con la misma altura los hombres tienen el pie más grande que las mujeres.

10. Si se entiende bien esta idea simple se entenderá perfectamente lo que persigue el Análisis discriminante. Porque esto es lo que hace la técnica: entre las variables de que disponemos y con las muestras que tenemos de las poblaciones en estudio debemos buscar qué variables y qué combinación de ellas es la que consigue separar más, discriminar más, esos grupos. La finalidad es usarlo como mecanismo para clasificar a un individuo futuro del que tendremos los valores que tiene de esas variables pero del que no sabremos a qué población pertenece.

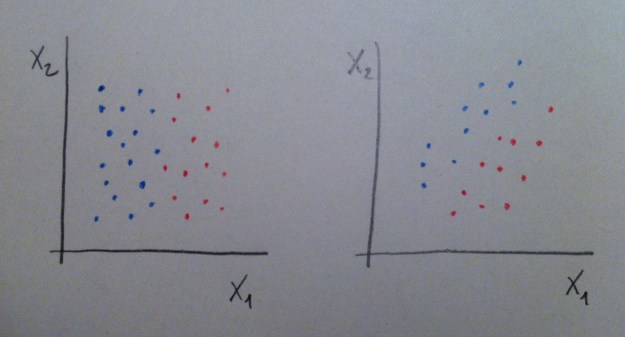
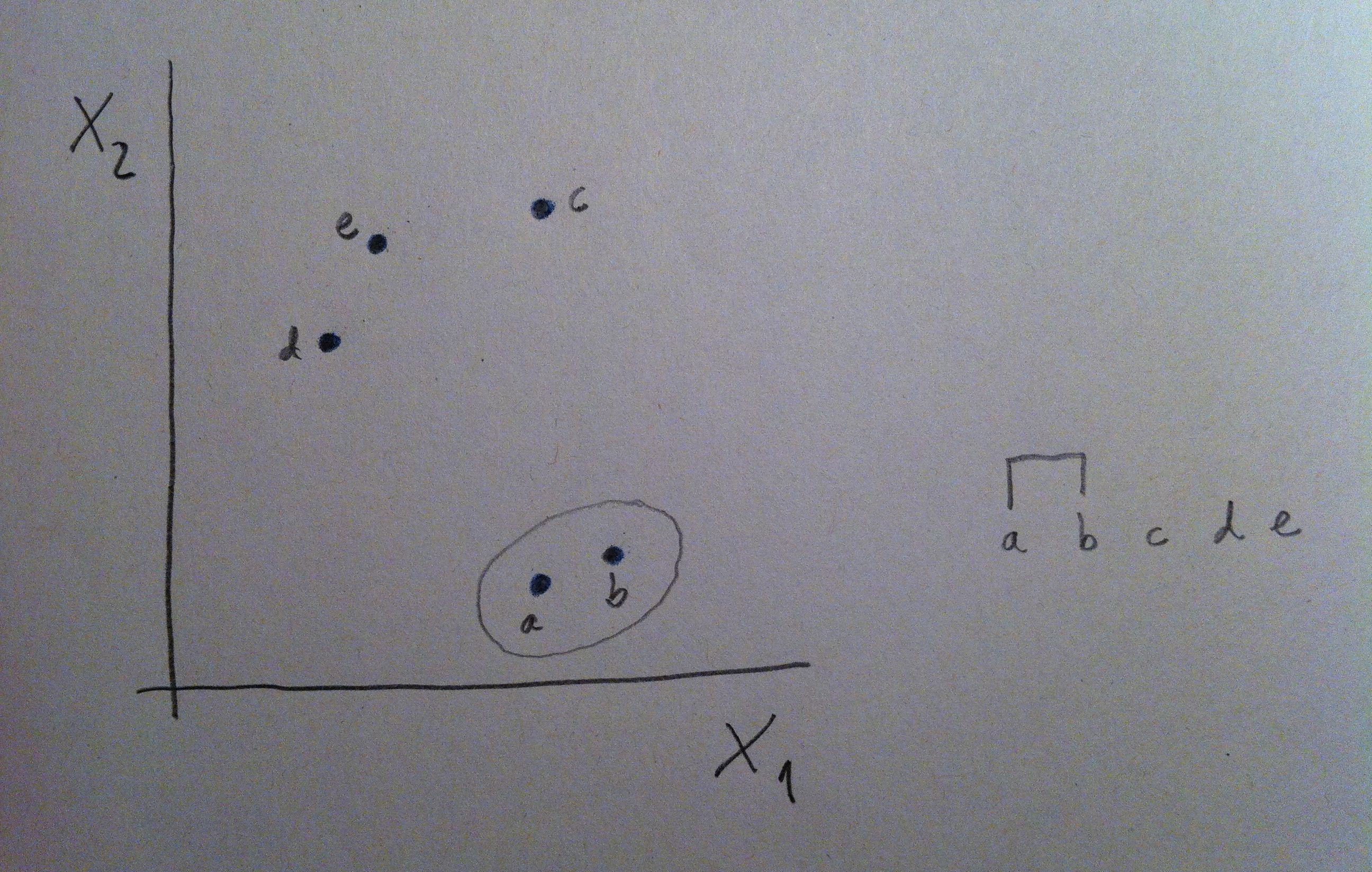
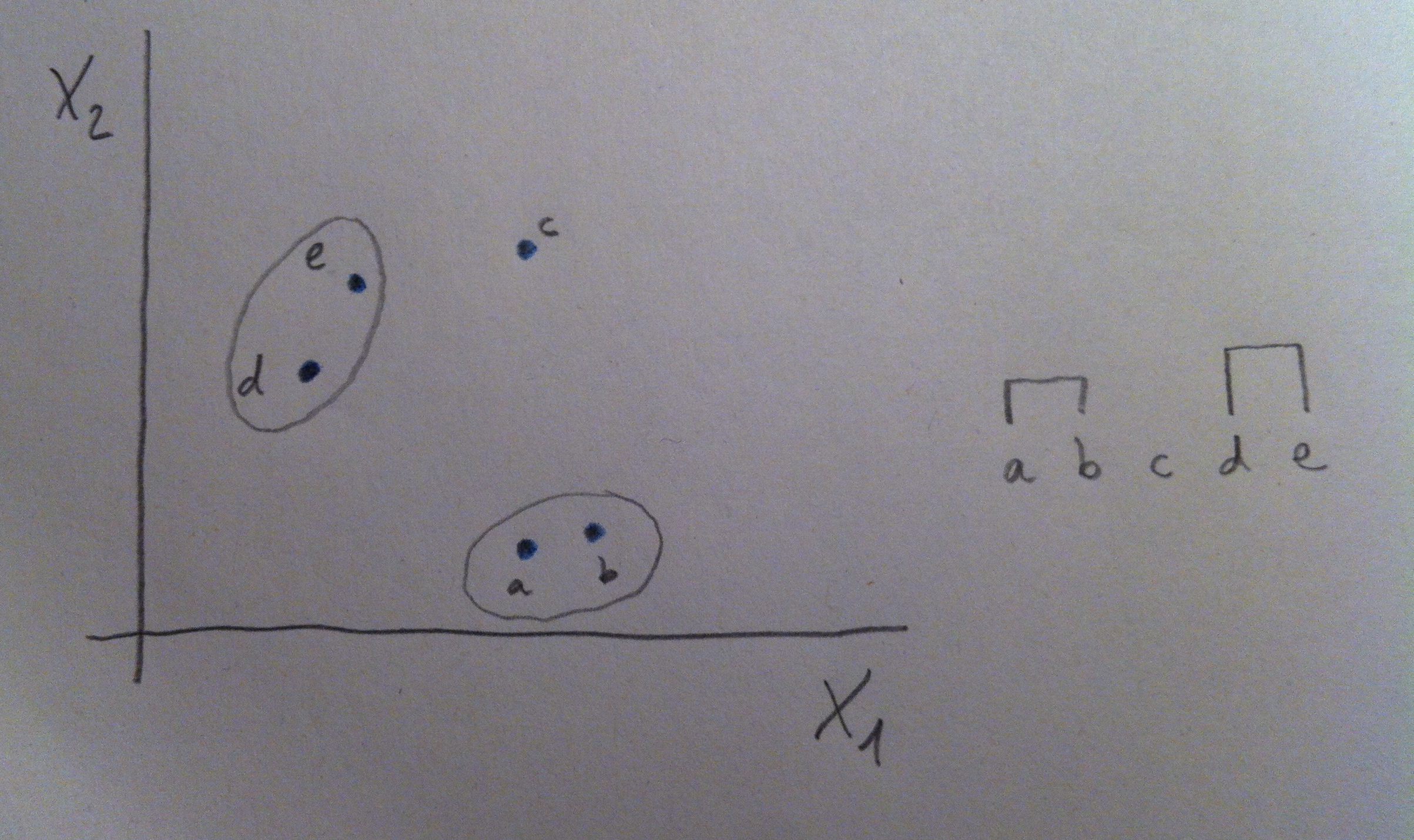
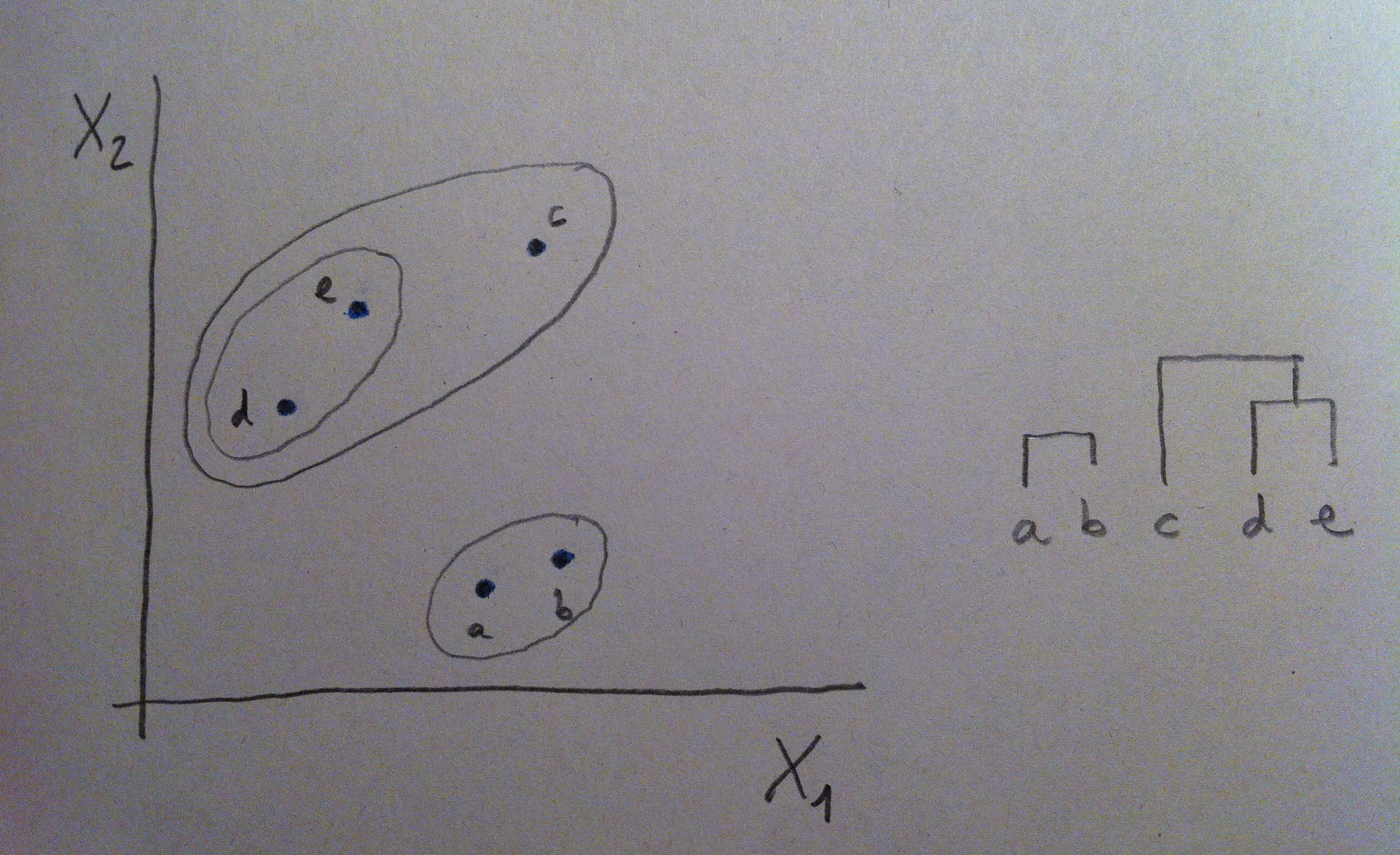
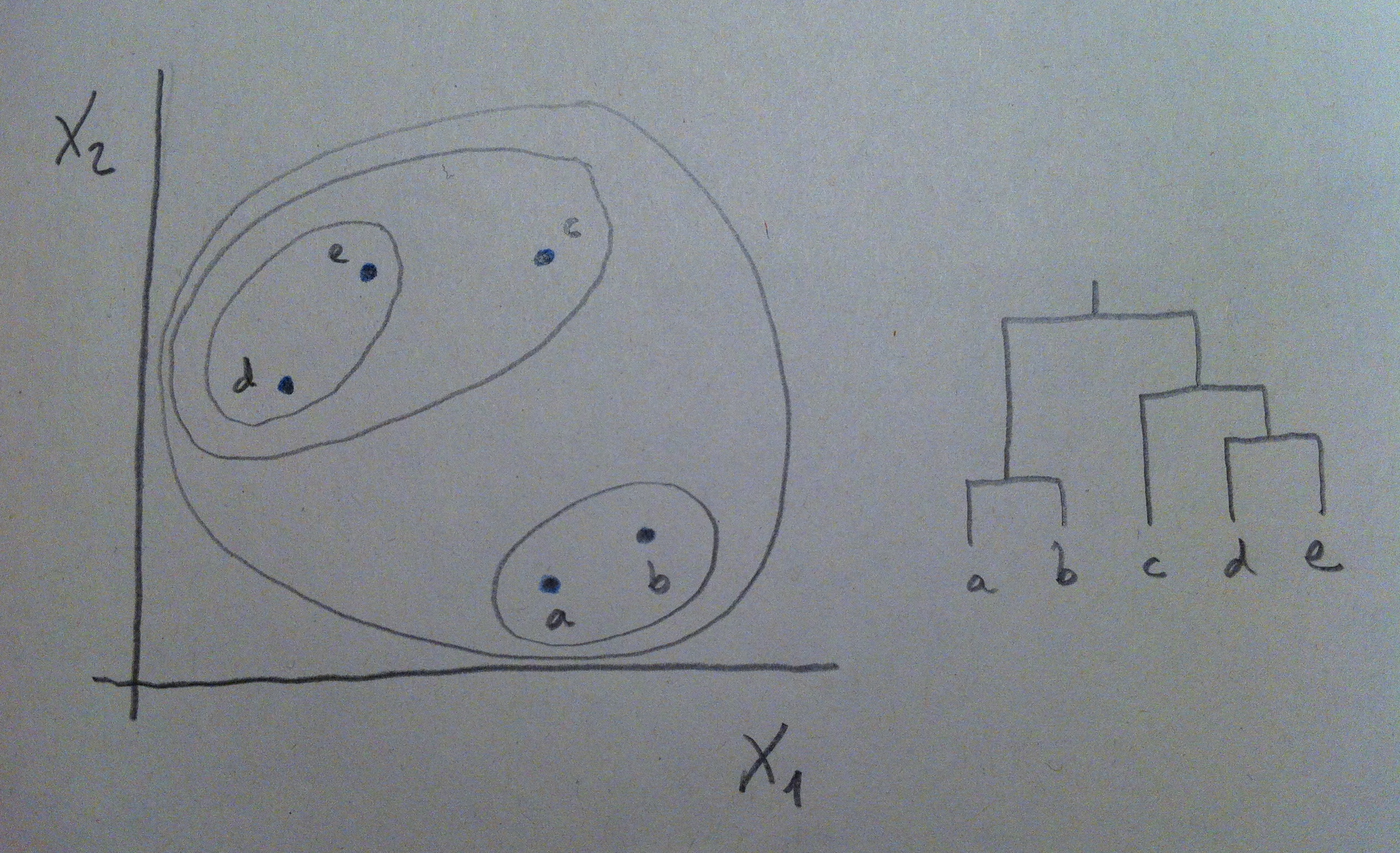
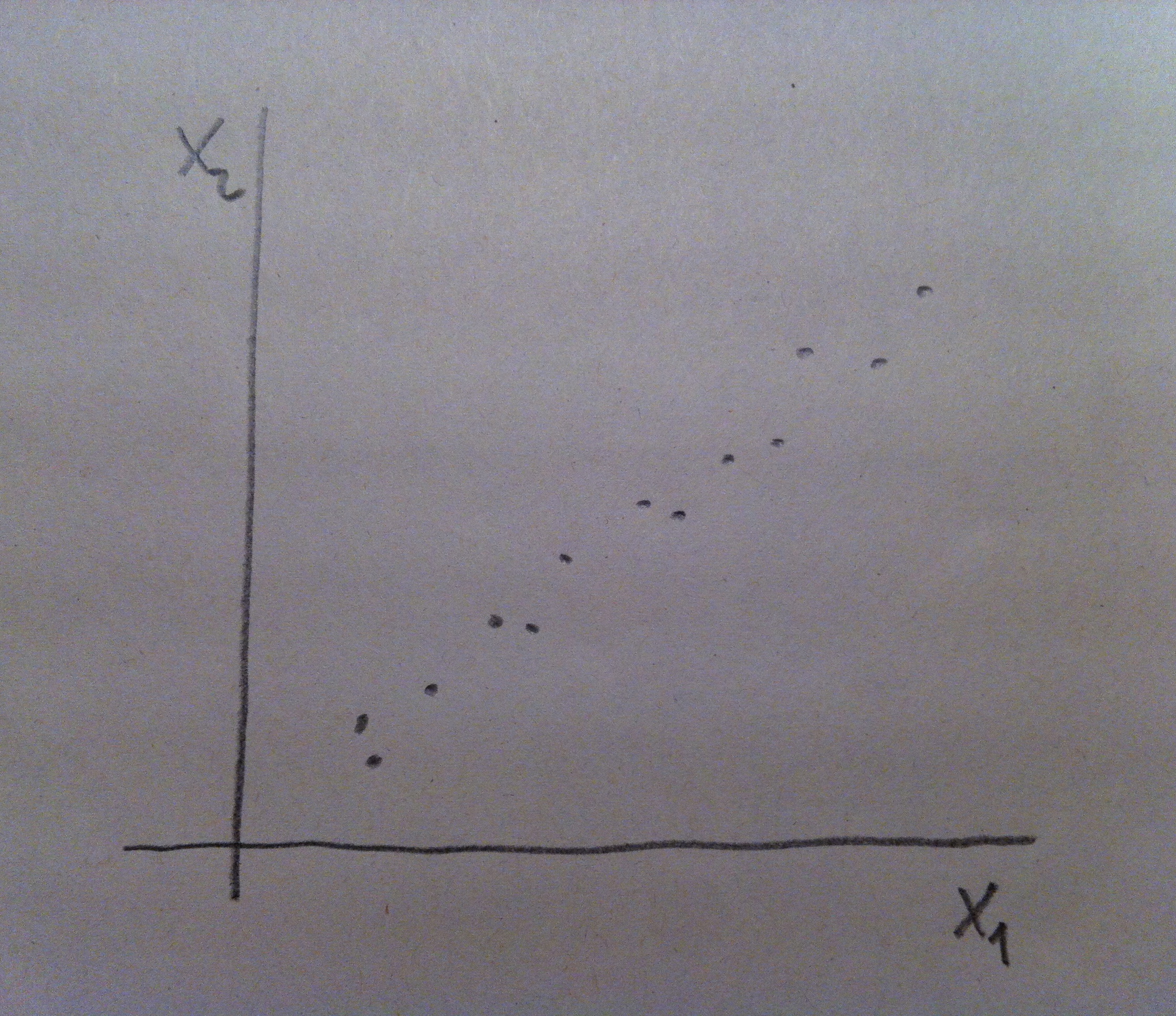
11. A veces si tenemos más de una variable con una de esas variables nos bastará para conseguir una buena discriminación, pero a veces ninguna de ellas individualmente nos irá bien y sí, en cambio, una combinación de ellas. Miremos el siguiente gráfico:

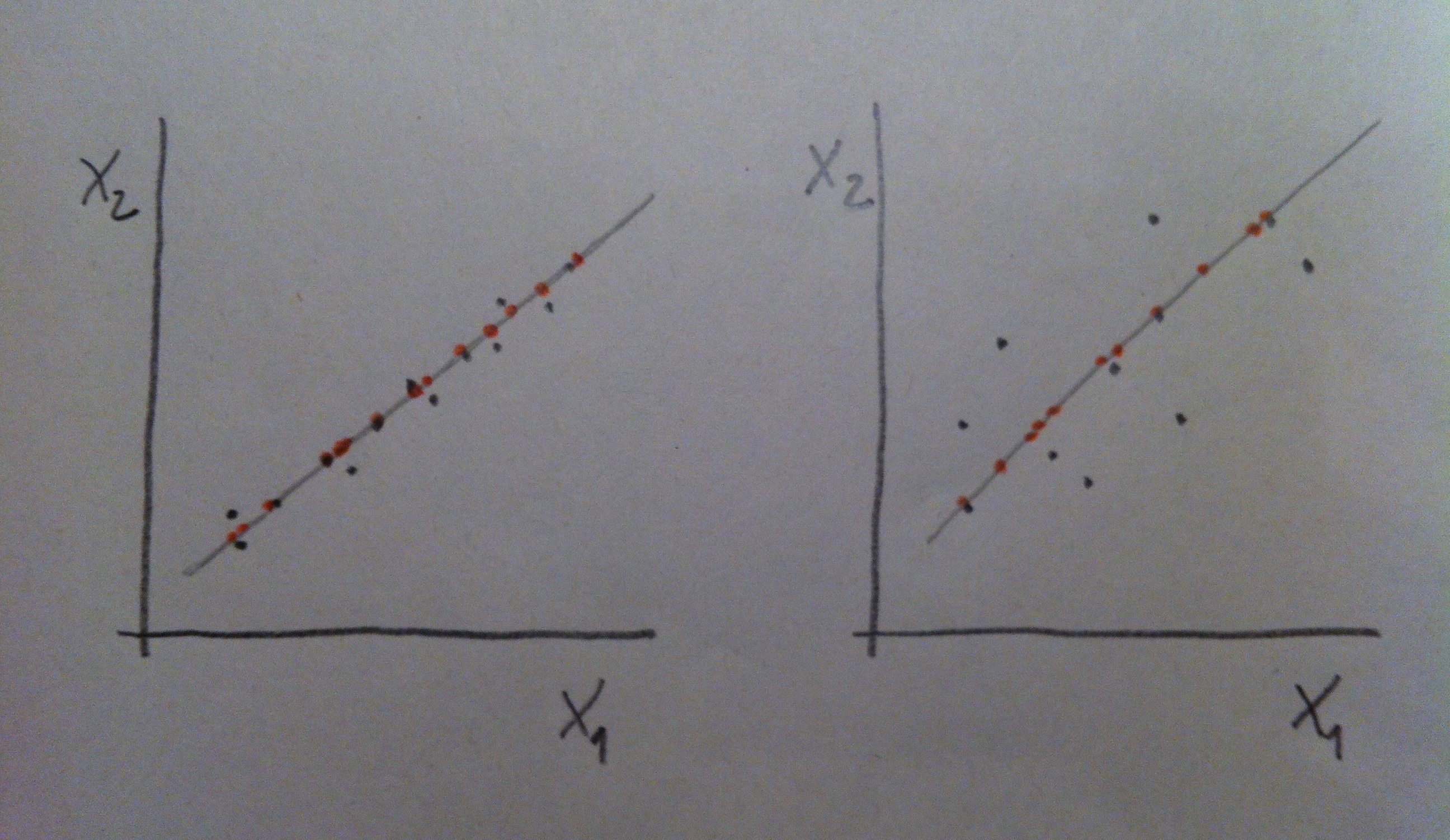
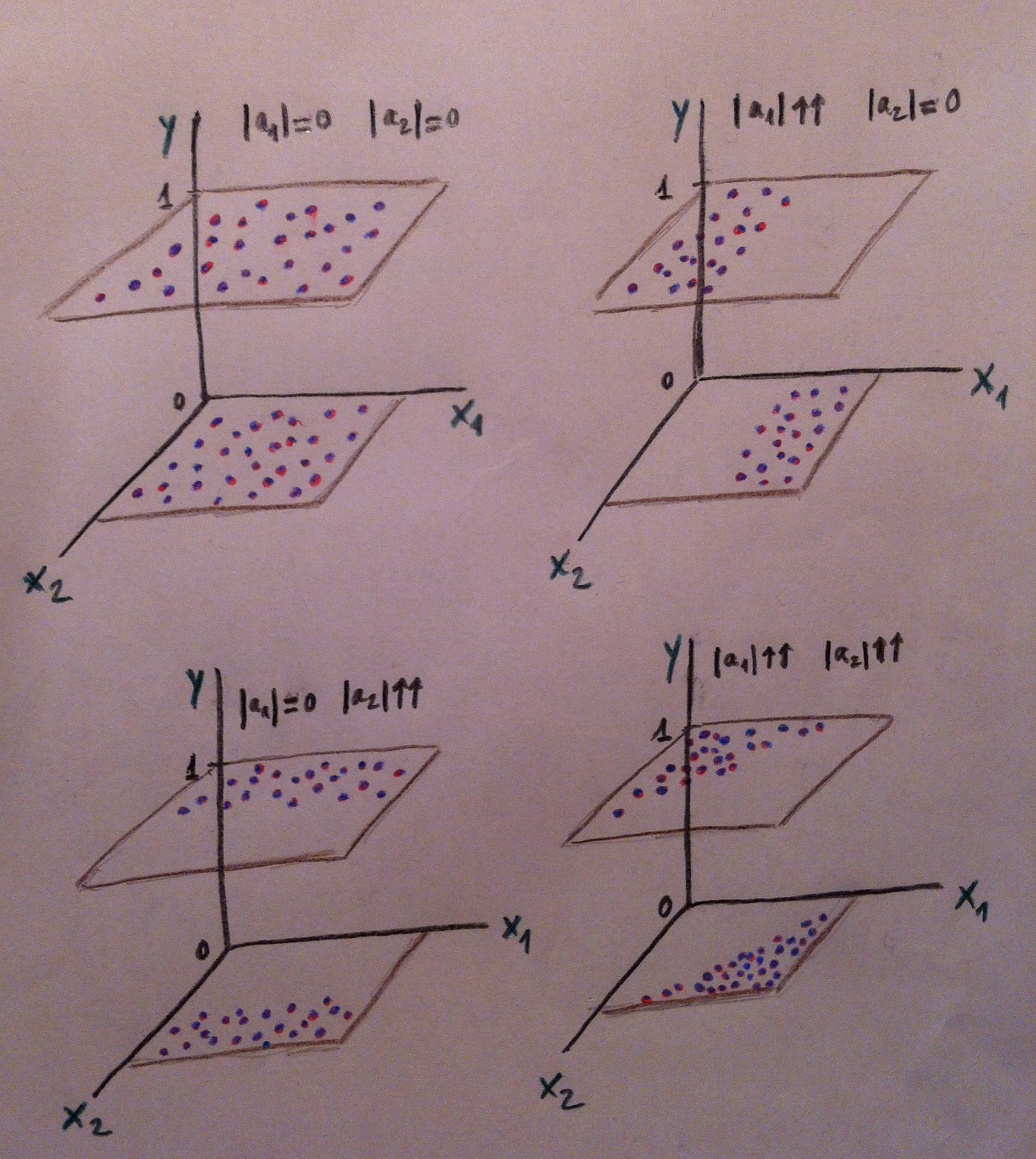
12. Puede observarse que en el caso de la izquierda la variable X₁ es muy buena discriminadora de las dos poblaciones: la roja y la azul. Desde X₁ las dos poblaciones se visualizan bien separadas. Tener el valor de X₁ de un individuo que no sabemos si pertenece a la población roja o a la azul nos permitiría, con cierta tranquilidad, clasificarlo de una u otra población y parece que la probabilidad de error sería bajo. En cambio la X₂ no discrimina, no nos separa las dos poblaciones. Esa variable es, pues, un mal referente para clasificar entre esas dos poblaciones.

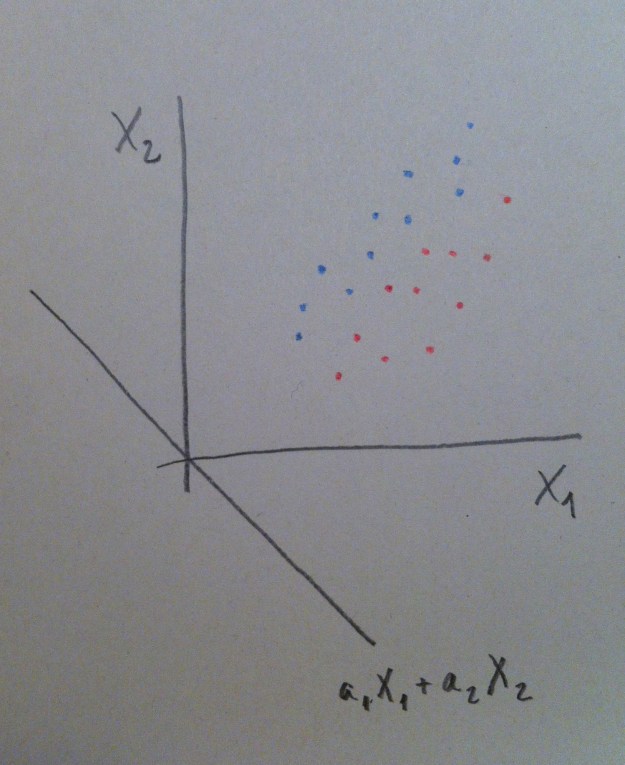
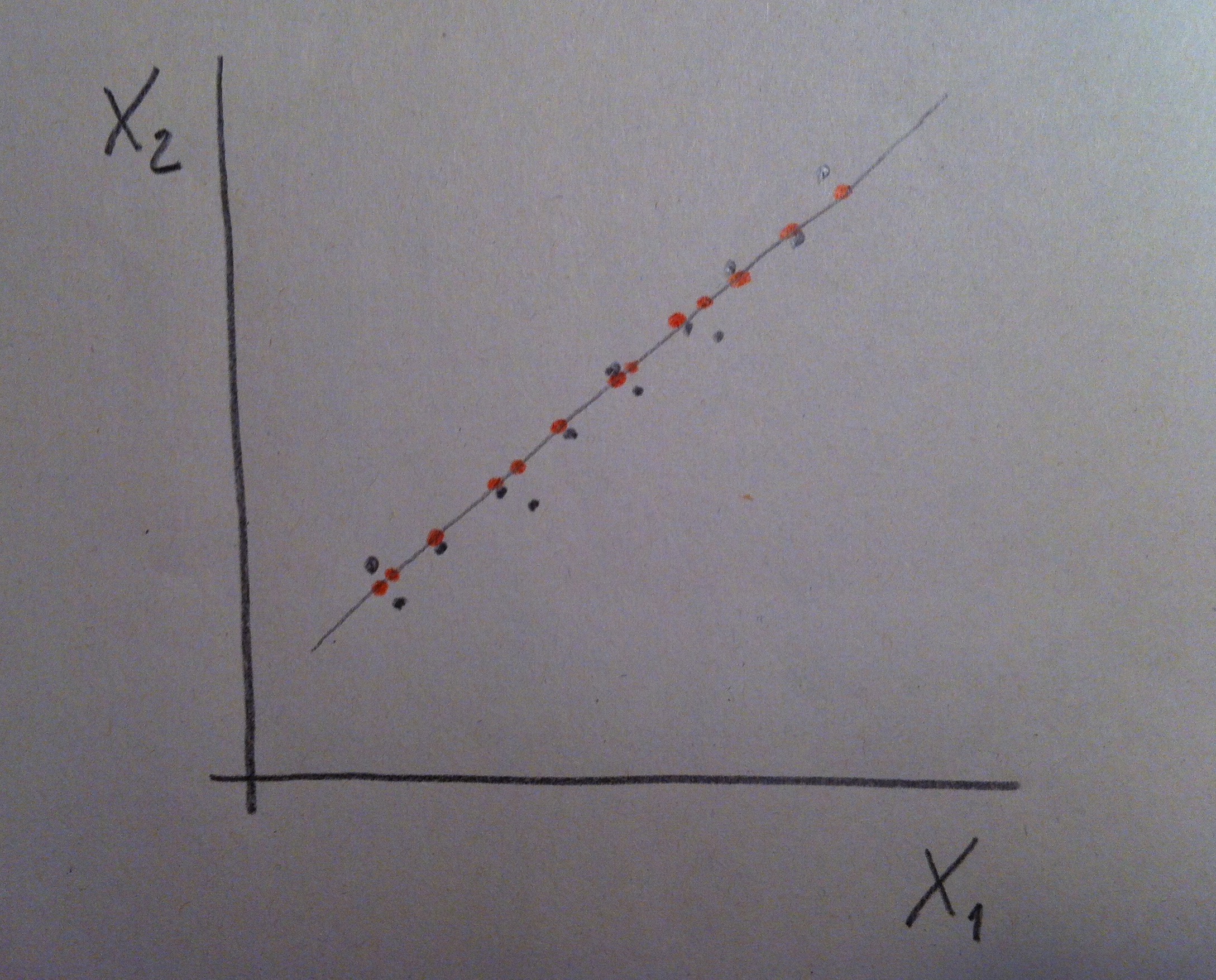
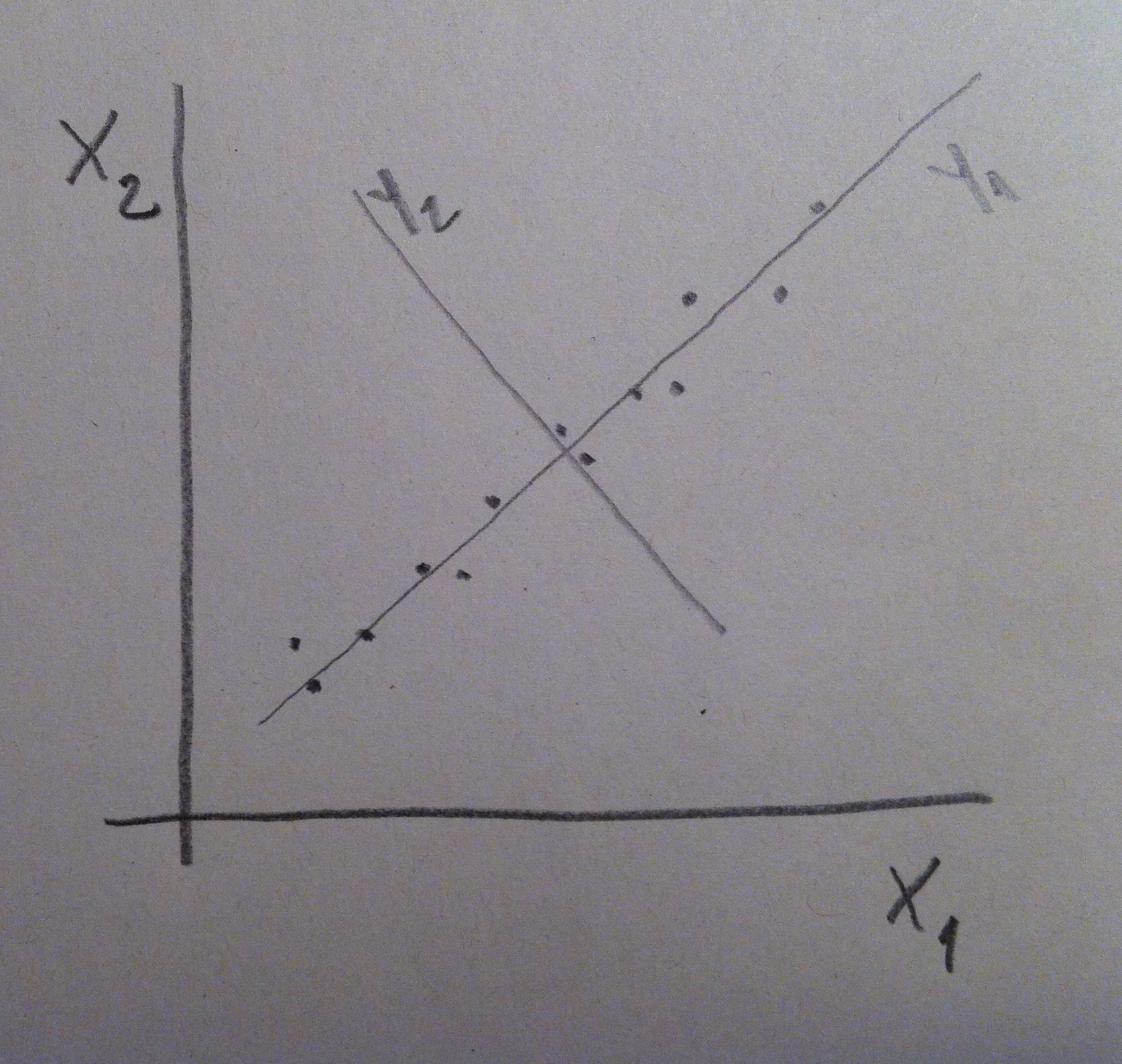
13. En el caso de la derecha del gráfico anterior la situación nos permite decir que ni X₁ ni X₂ son buenos discriminadores por separado. Si miramos la nube de puntos tanto desde X₁ como desde X₂ las dos poblaciones se ven mezcladas, no están discriminadas. Pero si hacemos un giro de los ejes, si hacemos una combinación de esas dos variables, podremos discriminar bien. Miremos el giro que hacemos en el gráfico siguiente:

14. Ahora la variable a₁X₁+a₂X₂ sí que discrimina bien. Ver la nube de puntos desde este nuevo eje nos permite visualizar las dos poblaciones bien separadas. Por lo tanto, el valor que tengamos de un nuevo individuo de esta combinación de las dos variables originales nos permitirá establecer un criterio de clasificación con pocas probabilidades de error. Y no olvidemos que hacer este giro va asociado de una fórmula como ésta, una fórmula que combina de una forma peculiar y lineal esos dos ejes originales.

15. De hecho, lo que acabamos de hacer no nos debe extrañar, lo hemos hecho ya en el Análisis de componentes principales y en el Análisis factorial. Hemos hecho combinaciones de las variables originales, hemos hecho giros de los ejes, hemos creado componentes, factores. Ahora, en el contexto del Análisis discriminante estas combinaciones de las variables originales las llamamos funciones discriminantes. Pero, en abstracto, es como una componente o un factor: una combinación lineal de las variables originales.

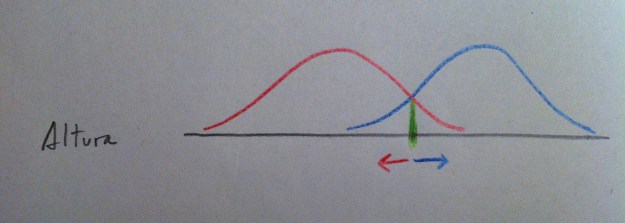
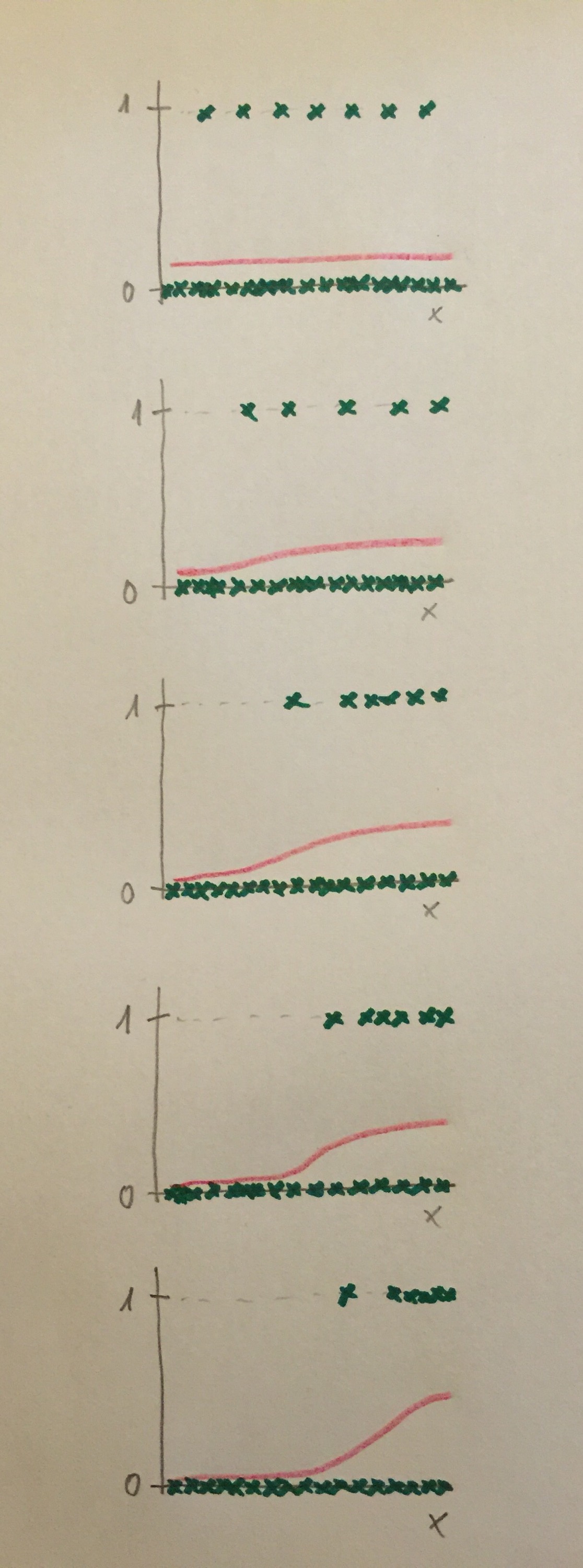
16. Y sea el tipo que sea de Análisis discriminante el que realicemos, de entre los que veremos a continuación, el procedimiento siempre es el mismo: se trata de crear un mecanismo de decisión a través del cuál al nuevo individuo se lo clasifica según el peso que tenga respecto a las densidades de las diferentes poblaciones. Lo veremos mejor con un ejemplo: Supongamos uno de los casos vistos antes: la altura como variable que discrimine entre hombres y mujeres. Lo que haremos es crear una función de densidad a partir de la muestra de hombres, otra a partir de la muestra de mujeres y entonces al nuevo individuo clasificarlo de la población que le tocaría más densidad; o sea, en el gráfico establecemos una frontera (en color verde) justo donde cambia la zona de mayor influencia de una u otra población. Si cae el nuevo valor a la derecha de esa frontera lo clasificamos de azul, si cae a la izquierda lo clasificamos de rojo:

17. Hay diferentes técnicas de Análisis discriminante. Hay el Análisis discriminante lineal, el Análisis discriminante cuadrático y hay, también, todo un repertorio de técnicas que se suelen encajar bajo la denominación de Análisis discriminante no paramétrico.

18. La creación de funciones discriminantes, combinaciones de las variables originales desde donde establecer buenos mecanismos de discriminación, tal como lo hemos planteado antes, es una idea ligada al Análisis discriminante lineal, pero es cierto que aunque los mecanismos usados por los diferentes tipos de Análisis discriminante son distintos, todos comparten la atmósfera general que he intentado transmitir hasta ahora.

19. El Análisis discriminante lineal y el cuadrático parten de una serie de suposiciones que no siempre se cumplen, por eso se han desarrollado una serie de técnicas que son válidas sin el cumplimiento de las suposiciones rígidas que exigen las técnicas paramétricas. La discriminación lineal y la cuadrática requieren que cada una de las poblaciones siga la distribución Normal multivariante. Además, la discriminación lineal requiere que la matriz de varianzas-covarianzas sea la misma en todas las poblaciones. La discriminación cuadrática, de hecho, está diseñada para no tener que soportar esta suposición.

20. Las técnicas no paramétricas en Análisis discriminante tratan, mediante métodos diferentes y muy imaginativos, establecer procedimientos de clasificación de los nuevos individuos dentro del conjunto de poblaciones candidatas.

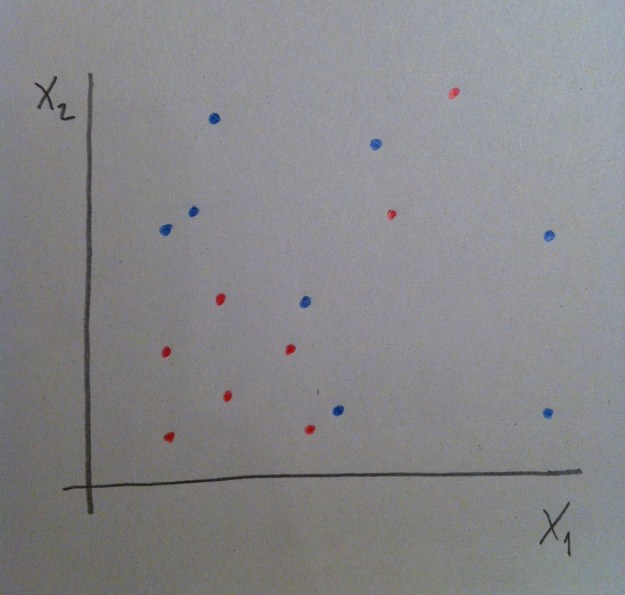
21. Uno de esos métodos no paramétricos de Análisis discriminante es el basado en la Estimación no paramétrica de funciones de densidad. Veamos un poco la operatividad de este método porque es conceptualmente muy sencillo e interesante. Supongamos los siguientes datos:

22. Tenemos dos muestras de dos poblaciones distintas: la roja y la azul. El método construye, entonces, para cada muestra, una función de densidad mediante el método Kernel y clasifica al nuevo individuo simplemente asignándolo a la población donde haya más valor de densidad, que querrá decir que por allí hay más influencia de esa población, hay más valores muestrales y, por lo tanto, parece lógico arriesgarse a clasificarlo de la población que tenga más representantes por la zona. Es la misma idea que la mostrada antes con la variable Altura pero en lugar de mediante una campana de Gauss, mediante una función de densidad estimada a partir de la propia muestra.

23. Como hemos dicho al principio del tema, y se ha podido comprobar a lo largo de su explicación, el Análisis discriminante es una técnica inferencial, una técnica que hace inferencias, que va más allá de lo que tenemos, que usa la muestra como medio para decir cosas que no sabemos. En este caso, para clasificar a individuos dentro de dos o más poblaciones.

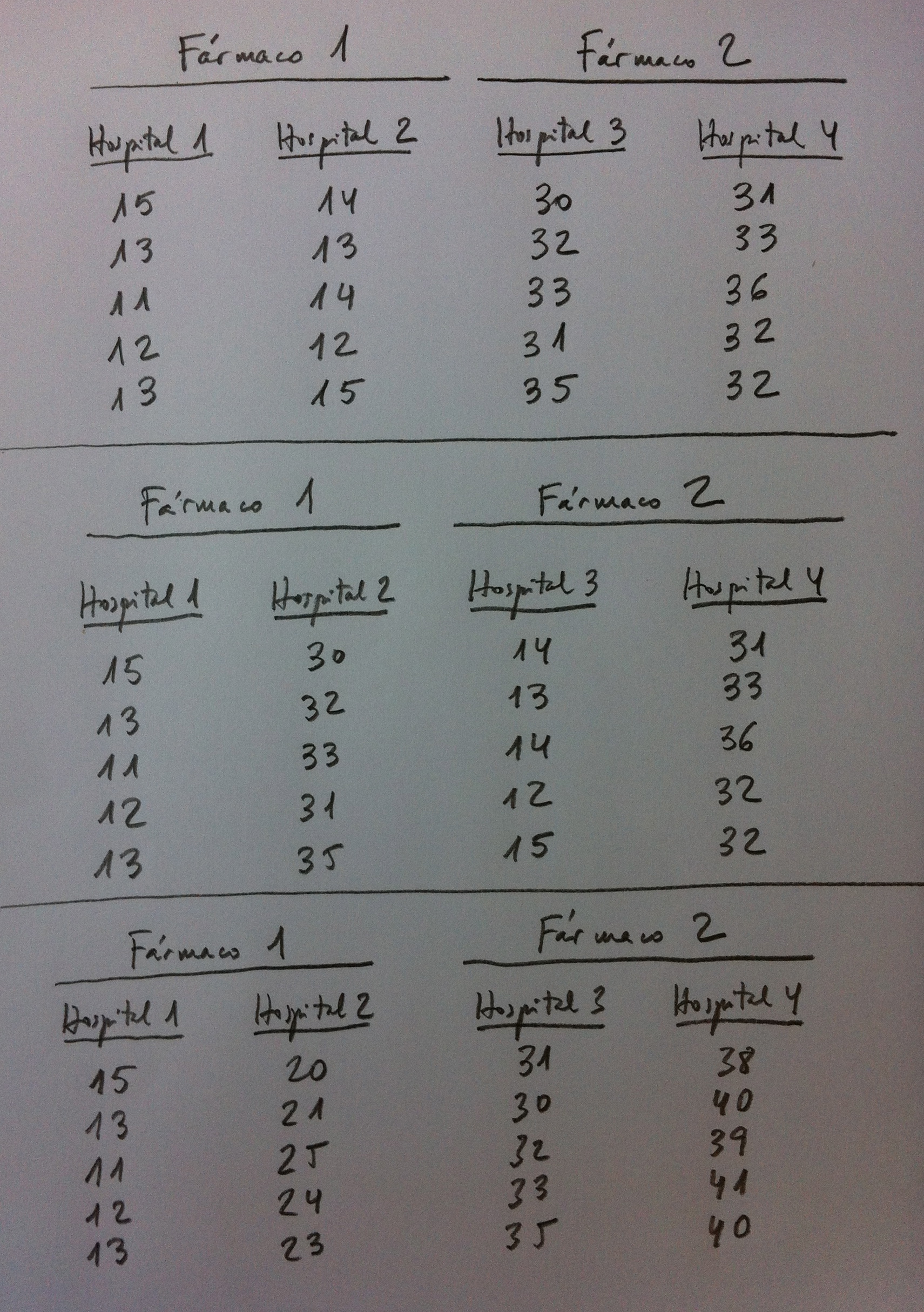
24. Veamos un ejemplo de Análisis discriminante lineal. Vamos a trabajar unos datos de años de supervivencia después del diagnóstico de cáncer de pulmón de células pequeñas. Los datos son los siguientes:

25. No vamos a entrar en detalles sobre cada una de las variables. Sólo decir que son típicas variables bioquímica y citológicas en una analítica sanguínea. La última columna es la Supervivencia, catalogada con tres valores: <1, 1-2 y >2, que representan: menos de un años, entre 1 y 2 años y más de 2 años. Esta es la columna que nos distingue las poblaciones. Son datos de enfermos que al diagnóstico tenían esta analítica y que acabaron sobreviviendo este tiempo especificado en la última columna.

26. El objetivo es, pues, aplicar el Análisis discriminante para establecer un mecanismo de clasificación, de pronóstico en este caso. Tenemos tres poblaciones definidas: Supervivencia de <1, de 1-2 y de >2 años. Tenemos tres muestras y 12 variables. Se trata de discriminar esas tres poblaciones, mediante esas 12 variables, con la finalidad de que a un nuevo paciente diagnosticado de esa enfermedad le podamos hacer un pronóstico con bastantes posibilidades de acertar.

27. En primer lugar deberíamos comprobar la normalidad de los datos y la igualdad de la matriz de varianzas-covarianzas. La normalidad multivariante es de compleja comprobación. Aunque la normalidad de cada variable individual no representa normalidad multivariante los software estadísticos acostumbran a comprobar esta normalidad univariante con cualquiera de las técnicas de bondad de ajuste a la normal, como el Test de Kolmogorov o el de la ji-cuadrado. Respecto a la homogeneidad de las matrices de varianzas-covarianzas una prueba habitual es el Test M de Box, que es una generalización del Test de Barlett univariante.

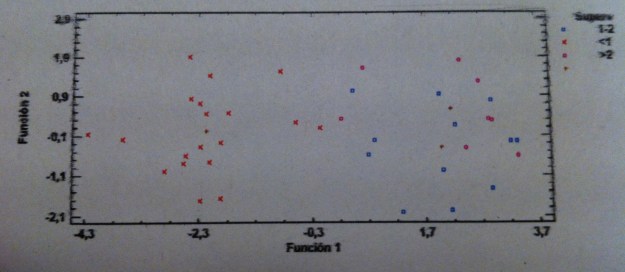
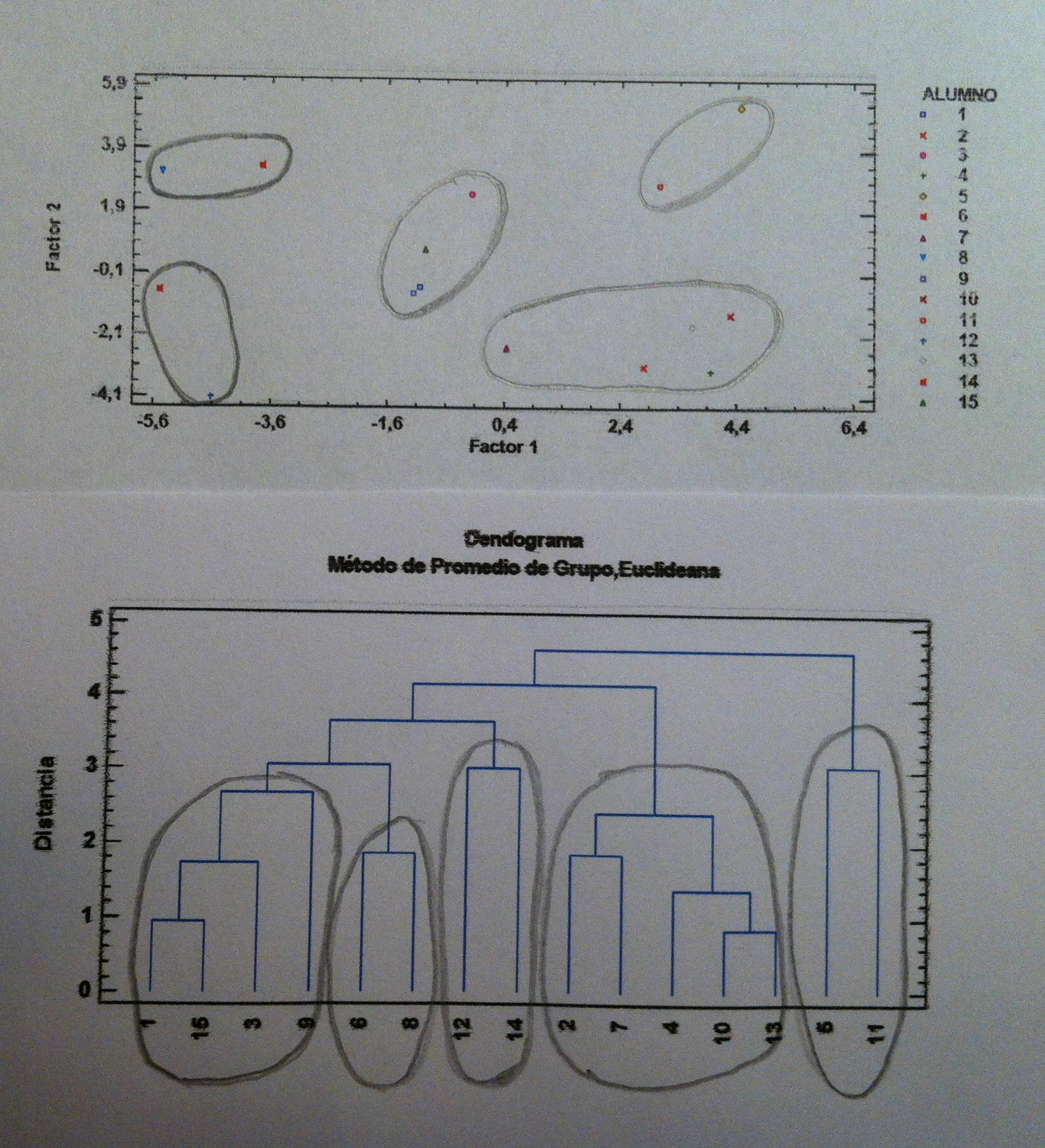
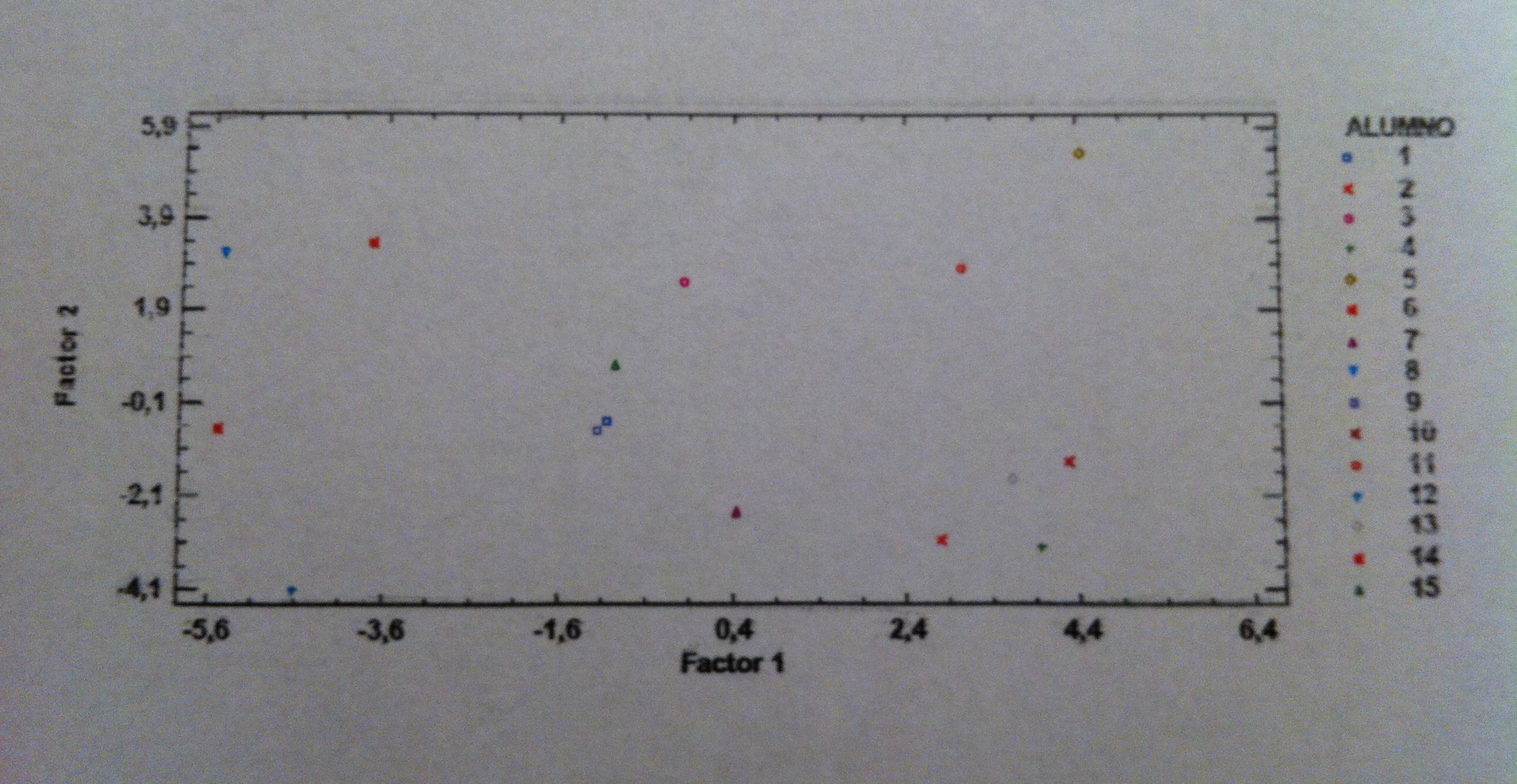
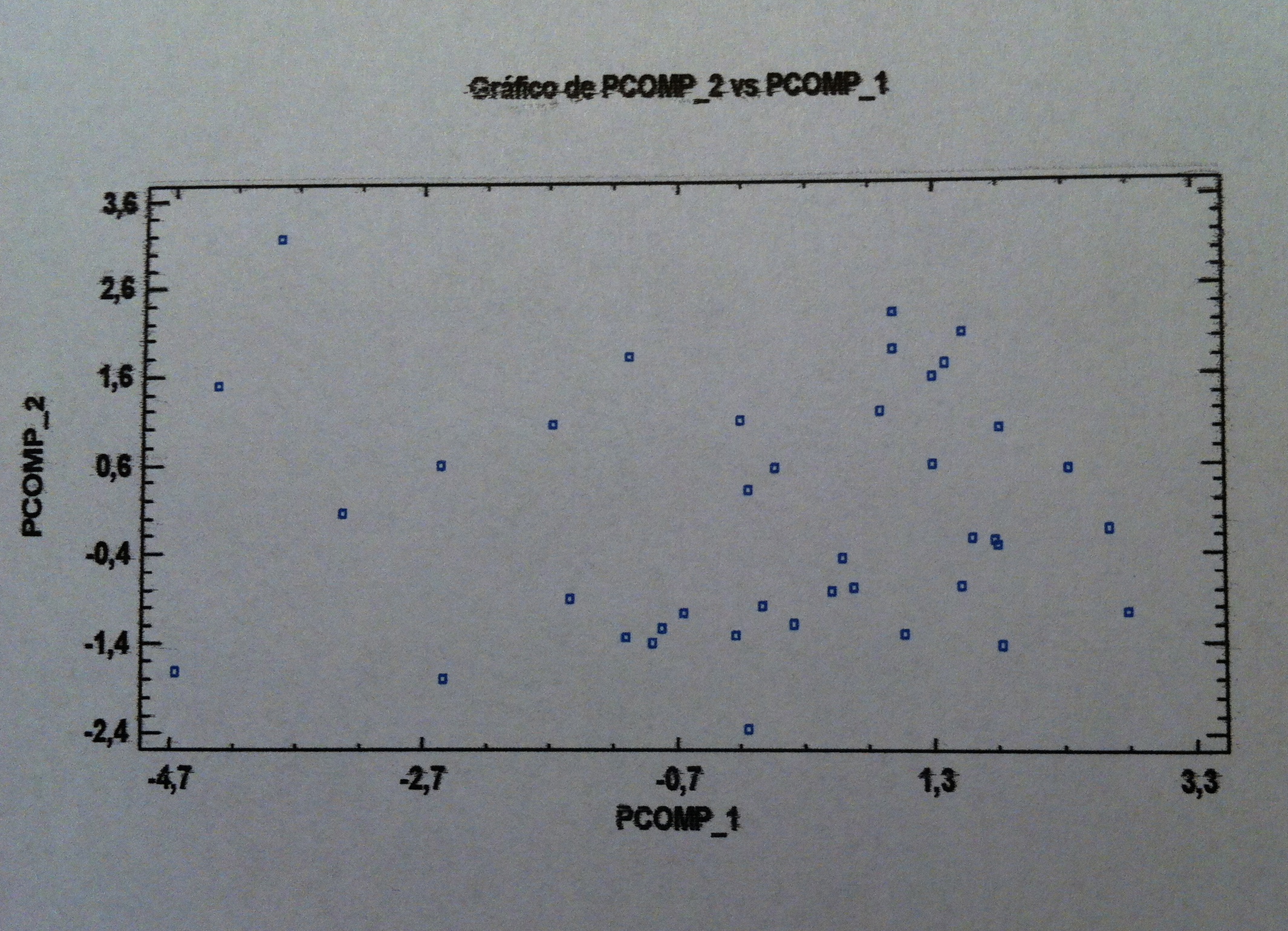
28. Una vez comprobadas estas suposiciones pasamos a la realización de un Análisis discriminante lineal. Dibujamos los datos mediante un gráfico en tres dimensiones con las dos funciones discriminantes que nos calcula el programa:

29. Las tres cruces que tienen forma de suma corresponden a los valores promedios de cada una de las tres poblaciones, de cada uno de los tres grupos de supervivencia.

30. De entrada, ya sólo viendo este gráfico y recordando lo que hemos dicho antes, parece claro que la Función discriminante 1 parece discriminar bien pero la Función discriminante 2 no parece que nos discrimine nada.

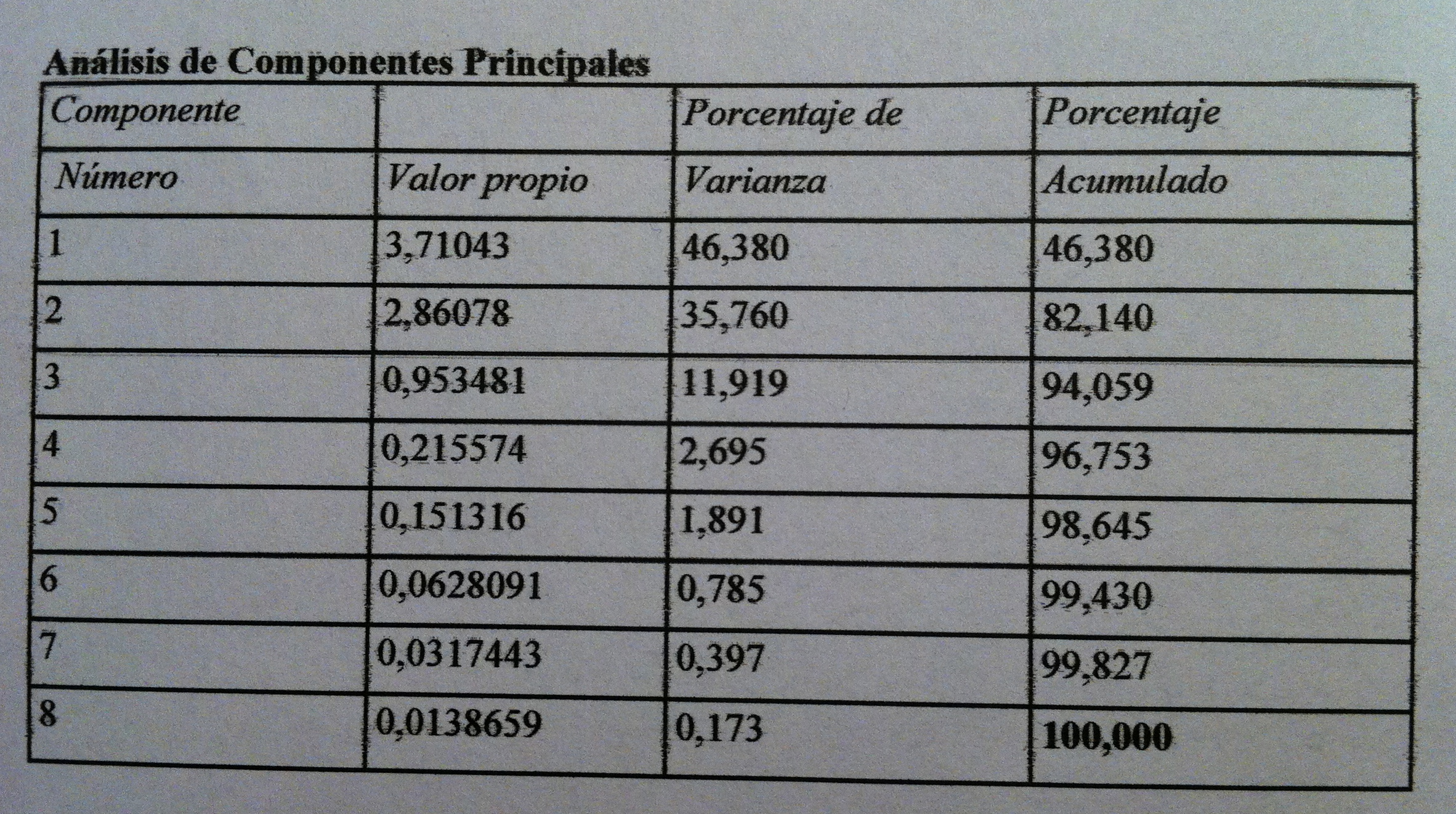
31. Veamos la siguiente tabla:

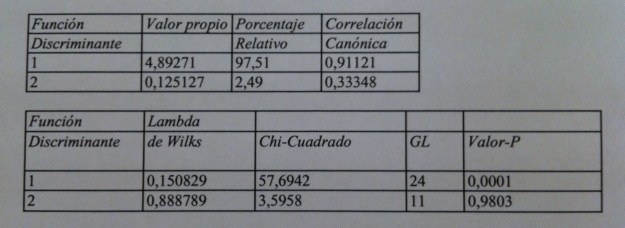
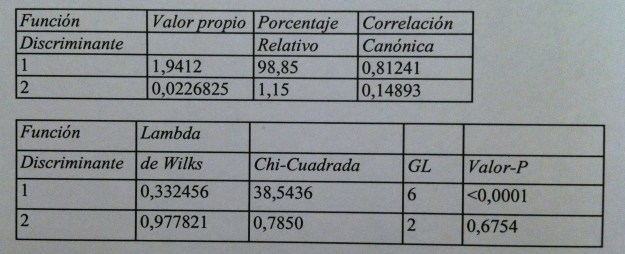
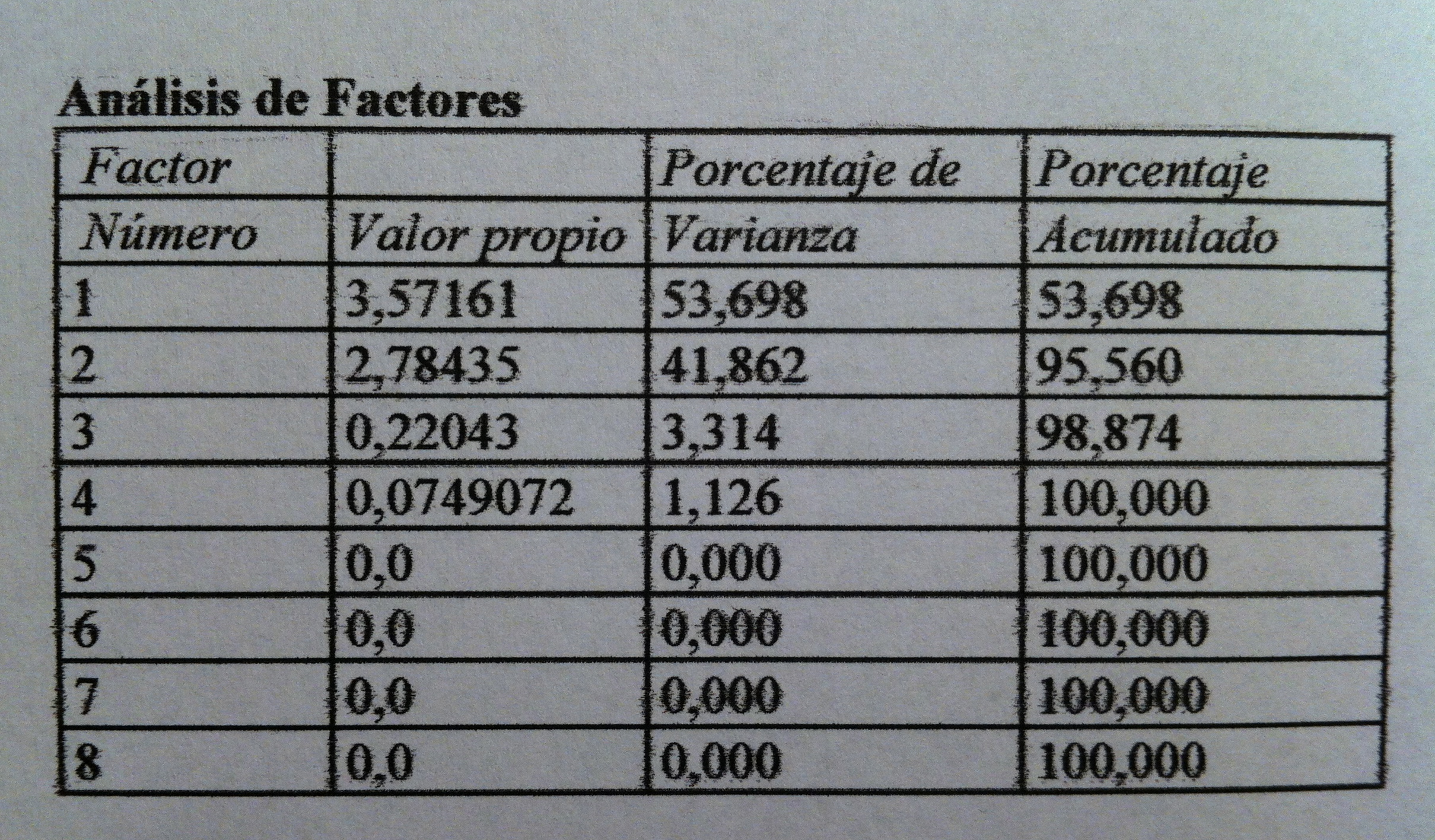
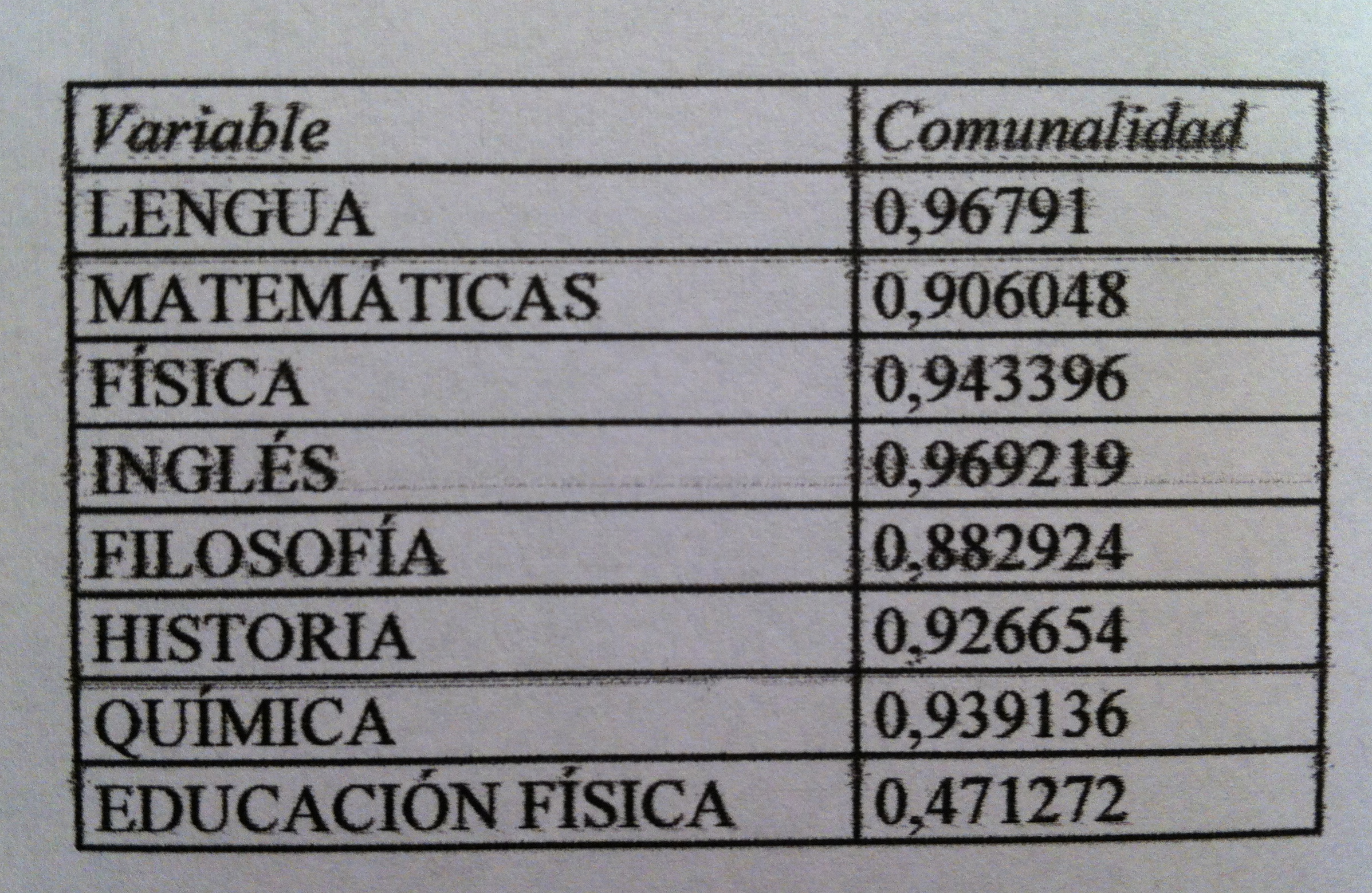
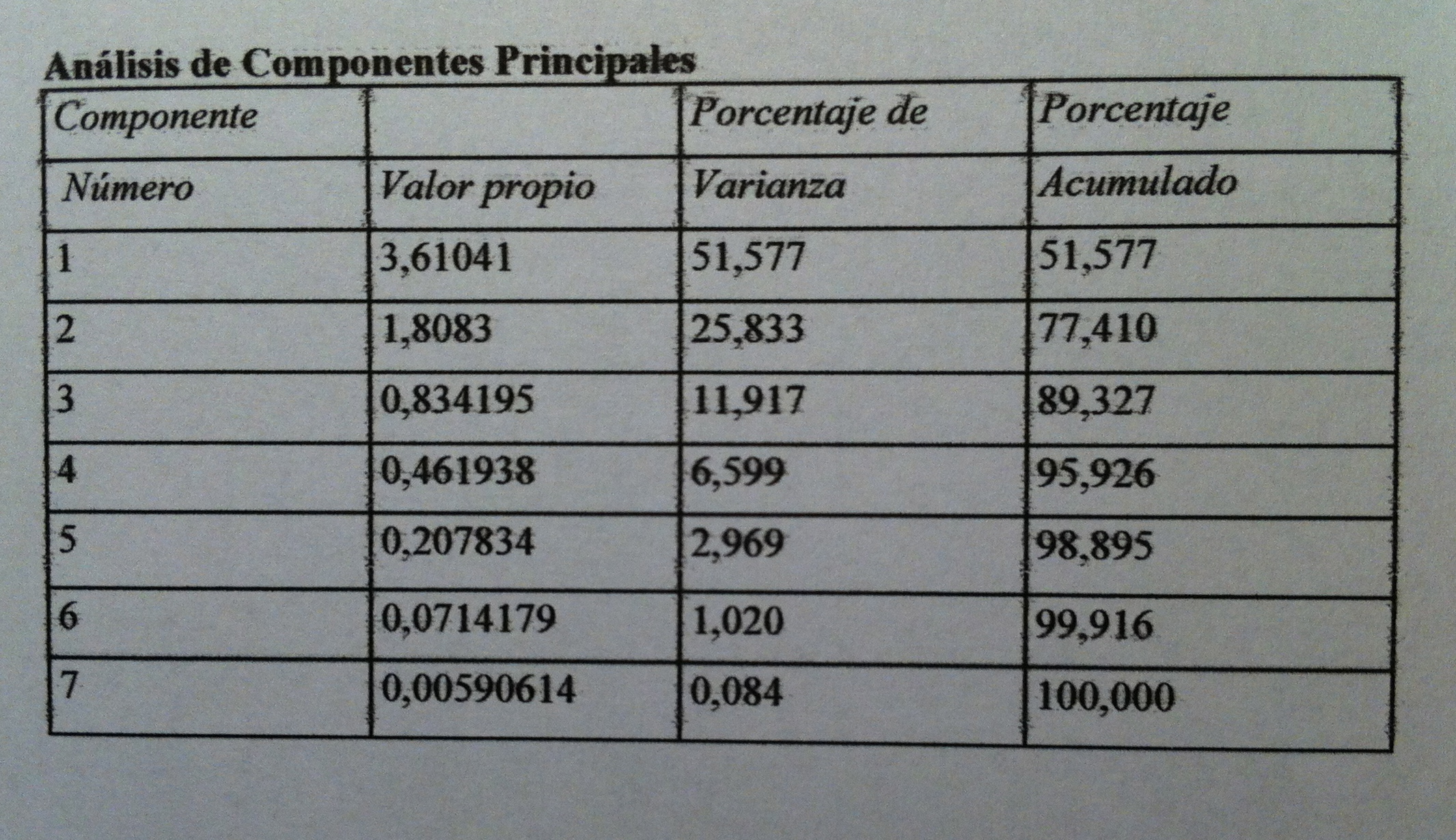
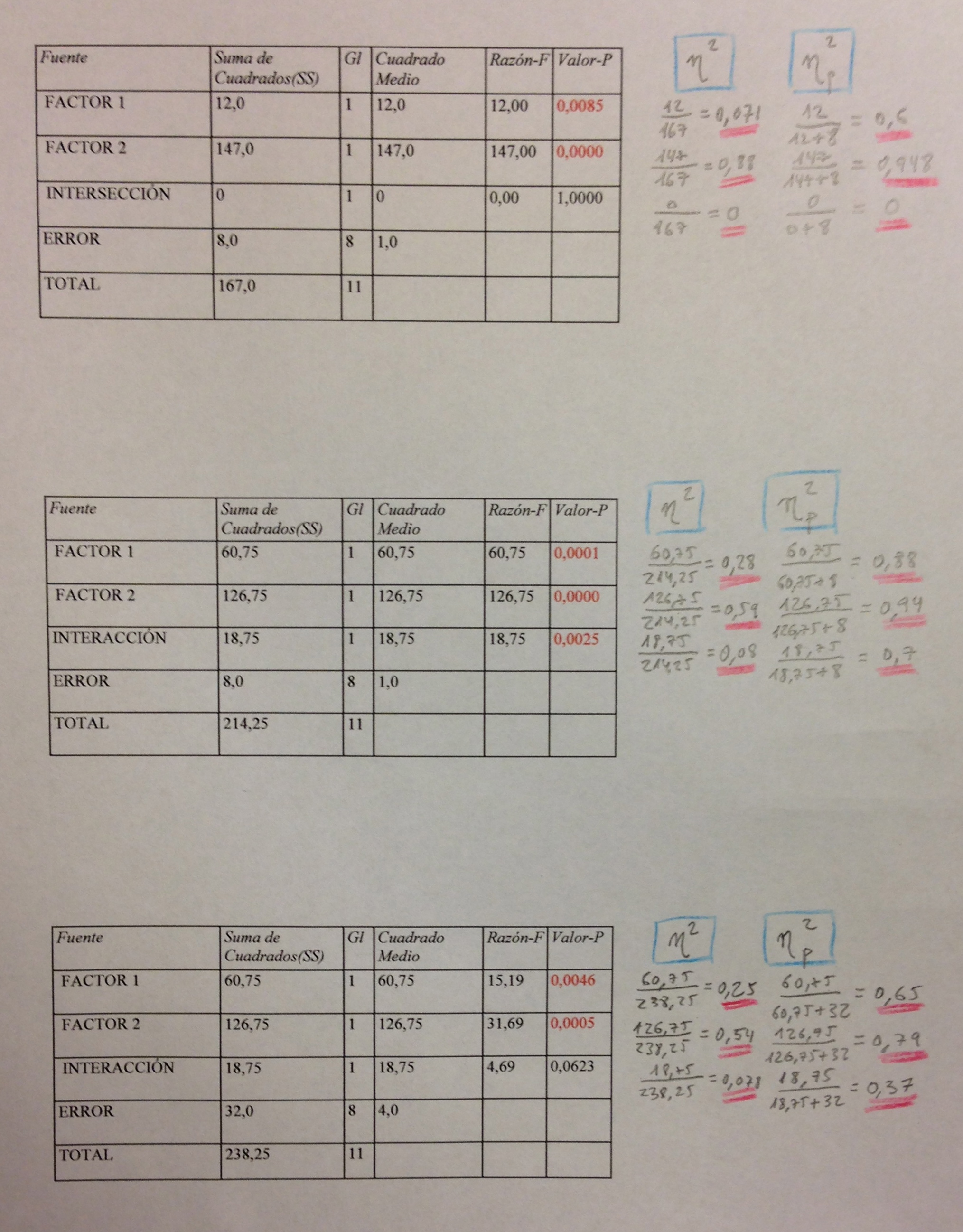
32.Los dos valores propios muestran que la primera función discriminante está mucho más relacionada que la segunda con los grupos de supervivencia. La correlación canónica así lo muestra también. Pero, además, gracias a la Lambda de Wilks podemos comprobar que, además, la primera función discriminante separa significativamente grupos, discrimina. Sin embargo, la segunda función discriminante no consigue una separación significativa. El Test de la Lambda de Wilks es básico en muchos ámbitos inferenciales multivariantes. Es un test que básicamente trata de establecer una relación entre la dispersión dentro de los grupos respecto a la dispersión total, sin tener en cuenta los grupos. Si

33. Veamos cuáles son esas funciones discriminantes:

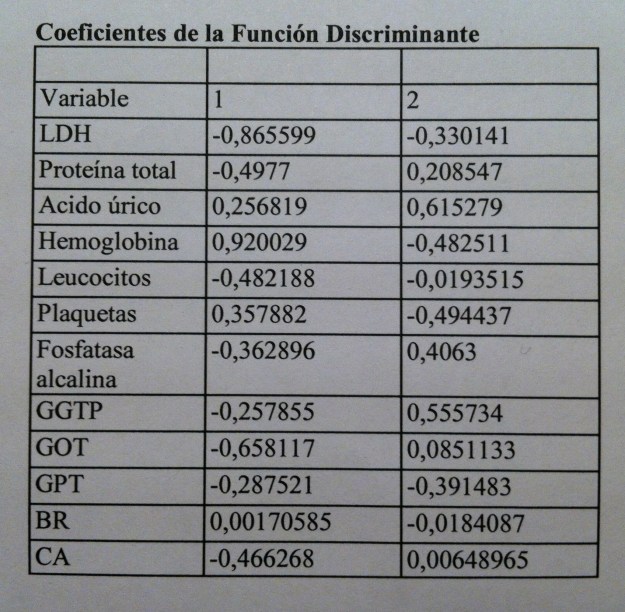
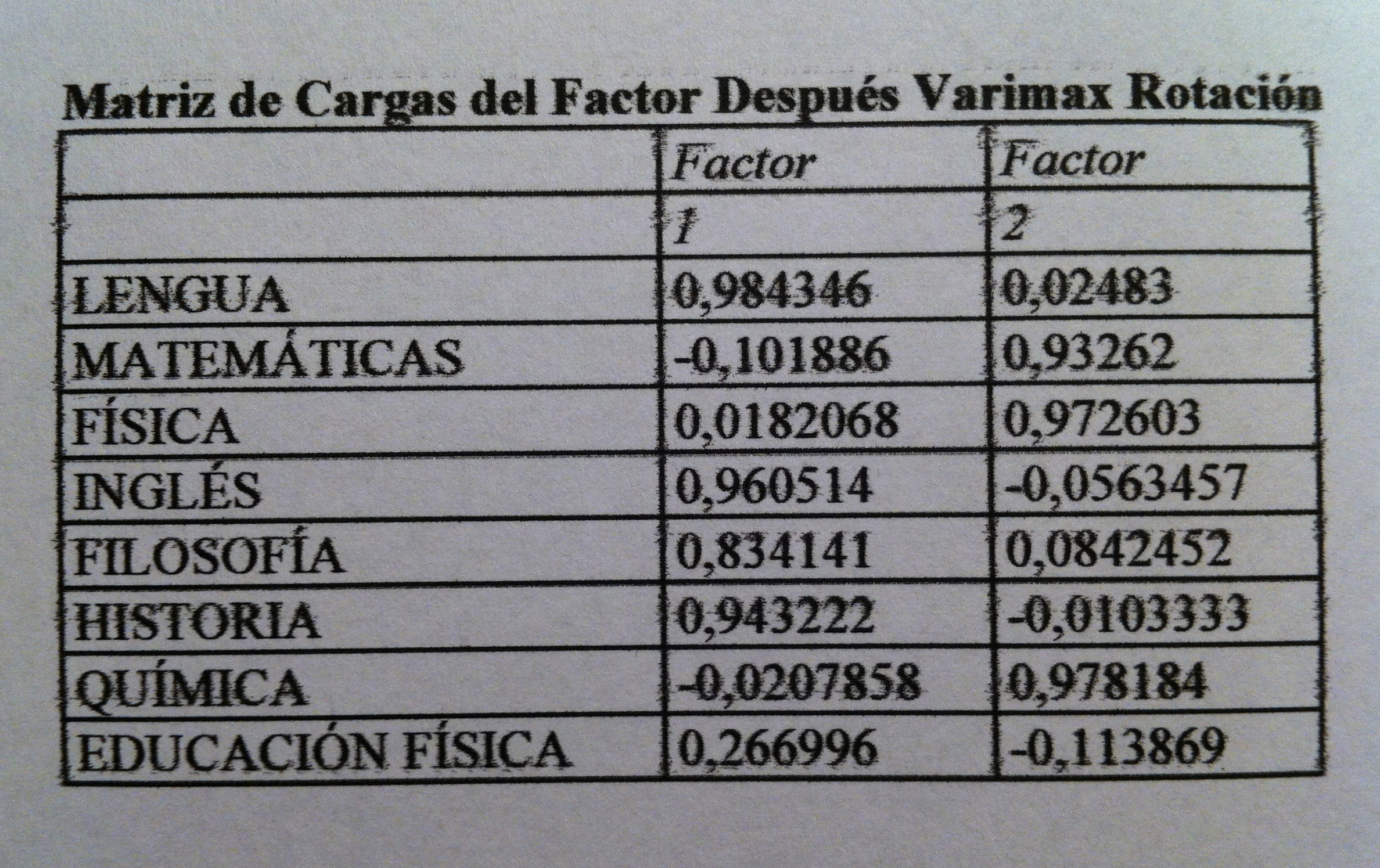
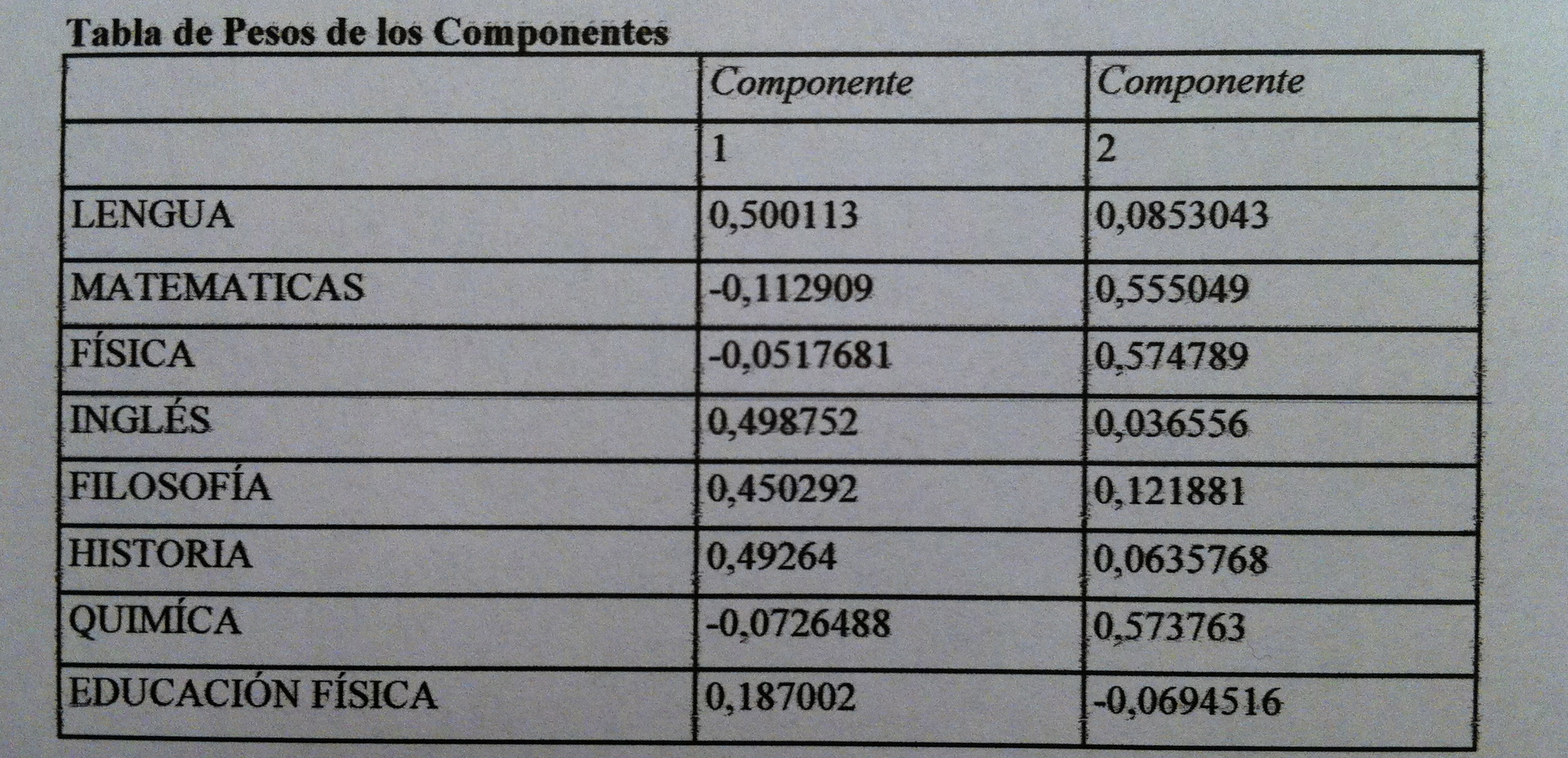
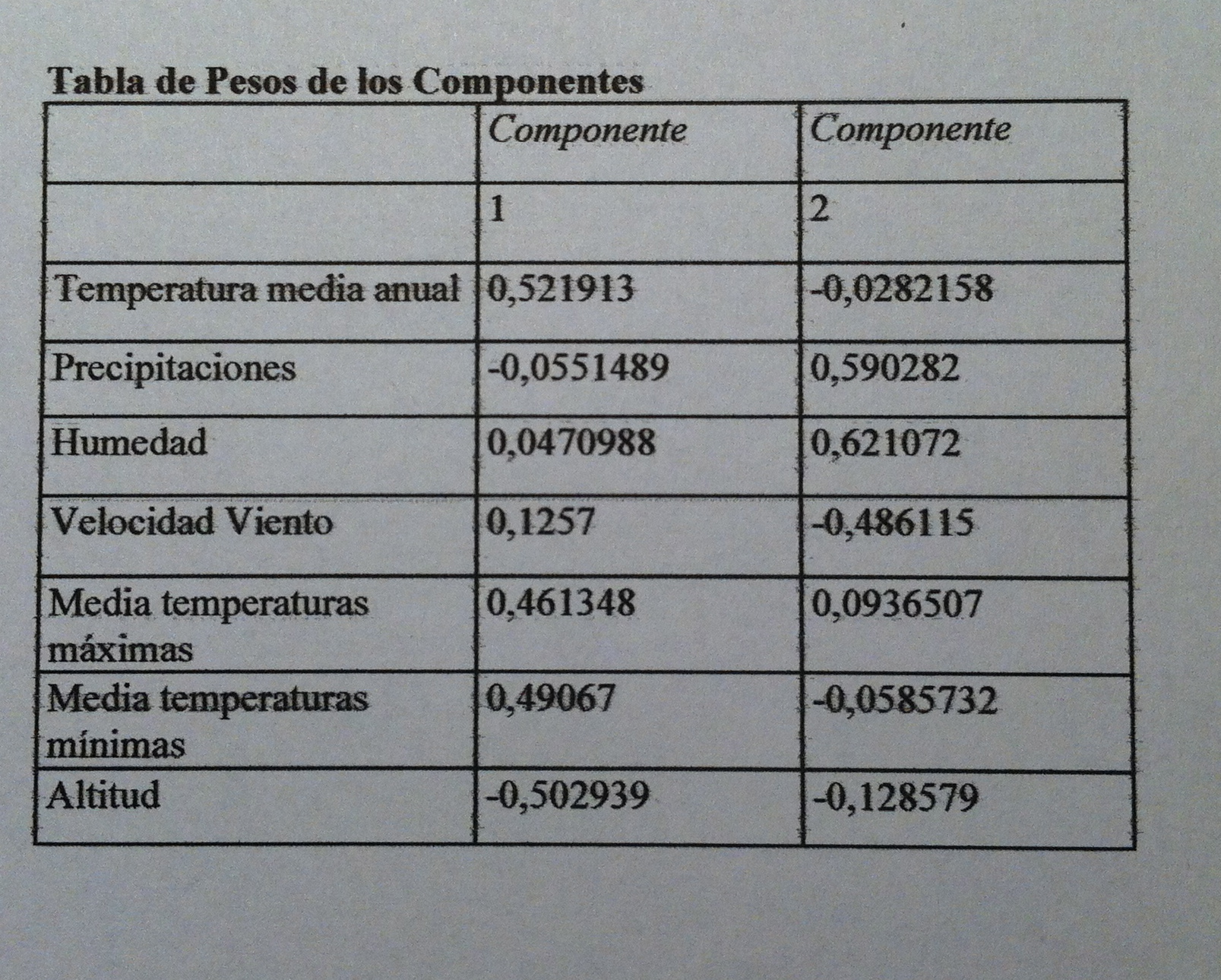
34. Tenemos las dos pero en realidad sólo debemos mirar la primera porque la segunda no nos discrimina. Como puede verse se trata de macrovariables, como las componentes o los factores. Pero ahora, debido al contexto donde las hemos creado las llamamos funciones discriminantes. El programa estadístico nos da dos pero sólo una es significativa.

35. En Análisis discriminante no suele haber una preocupación por la interpretación de esas macrovariables, de las funciones discriminantes. De hecho, el análisis está canalizado a la creación de un método que funciones, que sea útil, no suele haber un interés en ponerle nombre a esas funciones como sí ocurre, por el contrario, en Análisis de componentes principales o en Análisis factorial.

36. Para clasificar a un nuevo individuo diagnosticado de cáncer de pulmón de células pequeñas después de hacerle una analítica con todos estos parámetros deberíamos aplicar los valores de la siguiente tabla con las llamadas funciones de clasificación:

37. Estas funciones de clasificación de los nuevos individuos es creada a partir de las muestras que tenemos de los tres grupos de supervivencia. La operatividad es la siguiente: Se calculan los tres valores correspondientes para cada columna con los valores del individuo. El valor más alto es el valor más probable. Digamos que es una forma de calcular bajo qué distribución de las tres tiene más probabilidad.

38. Observemos que el procedimiento liga mucho con la idea del uso de Estimadores no paramédicos de la función de densidad con el método Kernel, comentado antes. Y, de hecho, liga con la idea nuclear que guía todo lo visto en este tema: hay que clasificar allá donde haya más influencia entre las muestras previamente establecidas.

39. ¿Cómo podemos cuantificar la eficacia del método de discriminación? ¿Cuál será su eficacia? ¿Podemos predecirla? Miremos este interesante método para hacer esta previsión:

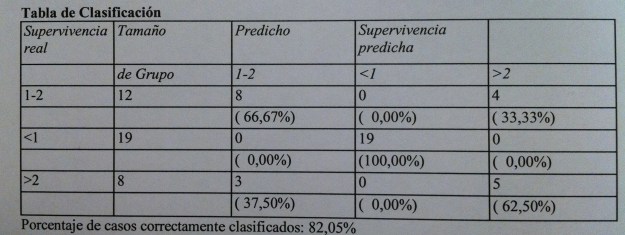
40. Se trata de un método ingenioso de estimación de la eficacia clasificatoria. Consiste en ir tomando uno a uno cada uno de los individuos de la muestra. Individuos de los que ya sabemos su supervivencia. Pues bien, aplicamos la tabla de clasificación establecida a partir de estos datos que hemos visto antes y miramos dónde quedaría clasificado este individuo si no supiéramos su supervivencia. Y esto lo hacemos con todos los individuos de la muestra. De esta forma tenemos de cada uno de los individuos dos valores de supervivencia: el real y el pronosticado. Construimos, entonces, esta tabla de clasificación donde vemos es las filas la supervivencia real (porque es nuestra muestra y la sabemos) y la supervivencia prevista aplicando nuestro método de clasificación. Así vemos si acertamos o no. Lo bueno es que los valores estén en la diagonal principal que es la que hace coincidir grupo real con grupo predicho. De esta forma se acaba calculando un porcentaje de casos correctamente clasificados, que, en nuestro caso, es del 82.05%. Que no es malo debido a la complejidad de los que estamos hablando.

41. Observemos que hemos trabajado con todas las variables del estudio. Pero aquí, en Análisis discriminante lineal también podemos hacer una Selección de variables hacia adelante o hacia atrás, como en la Regresión múltiple. Si hiciésemos esto a estos datos obtendríamos, en primer lugar, la siguiente representación de los individuos según las dos funciones discriminantes:

42. Los valores de significación siguen marcando la primera función discriminante como única función que discrimina realmente:

43. El proceso de selección del modelo encuentra que con tres variables basta. Con las variables LDH, Hemoglobina y GPT ya es suficiente. Las funciones discriminantes son:

44. La tabla de funciones de clasificación es ahora la siguiente:

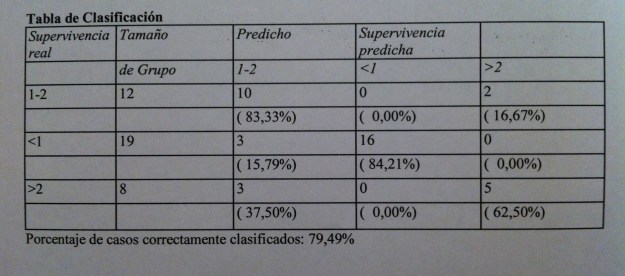
45. Y la tabla de clasificación que nos mide la calidad de la clasificación con los valores muestrales es la siguiente:

46. Tenemos un 79.49% de aciertos, un poco menor que el 82.05% de antes, pero con muchas menos variables.

47. Un breve comentario para acabar: Es interesante establecer conexiones entre el Análisis discriminante y la Regresión logística. De hecho, tienen profundas similaridades. De hecho, se trata de dos formas de enfrentarse a lo mismo. Observemos que las poblaciones en las que queremos clasificar a un nuevo individuo se puede ver, en realidad, como una variable cualitativa. Y el procedimiento de discriminación es como la búsqueda del modelo de regresión.

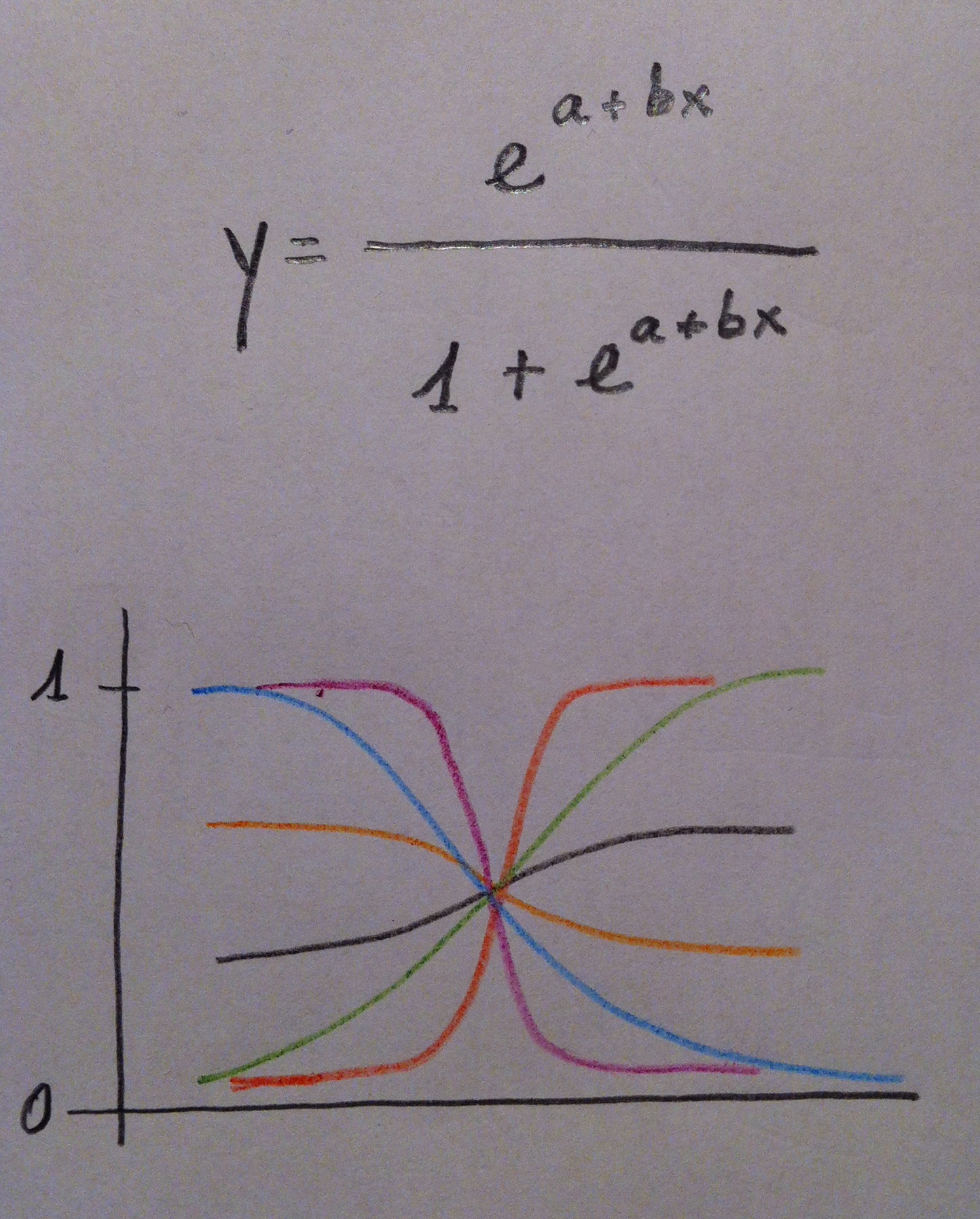
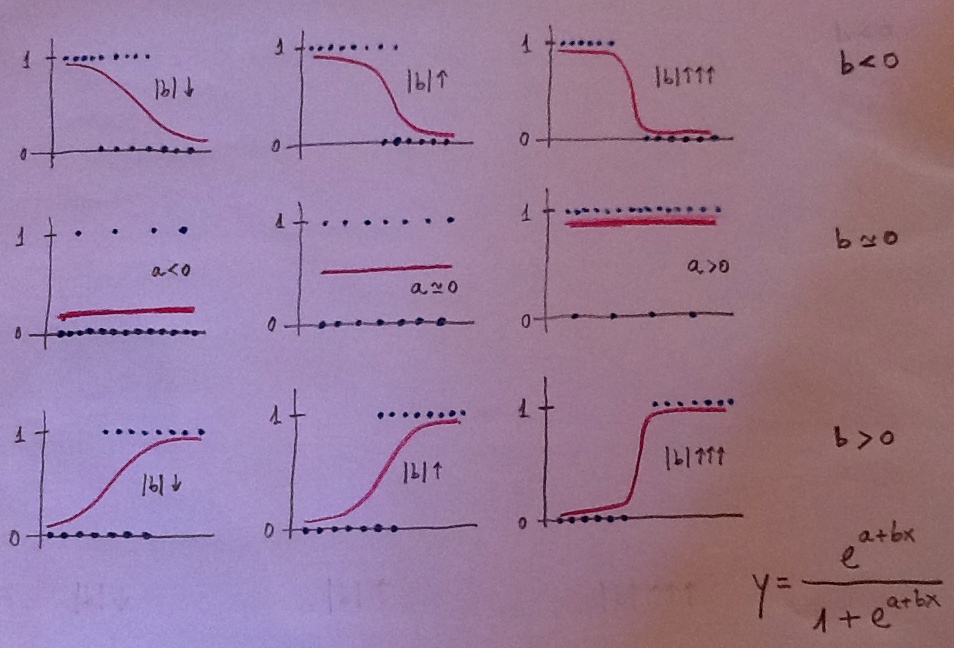
48. Cuando la variable es dicotómica y se pretende modelizar la situación y establecer relaciones entre la variable dicotómica y un conjunto de variables predictoras mediante Odds ratio, entonces es más habitual usar la Regresión logística. Cuando hay más de dos poblaciones y además hay especialmente una voluntad práctica clasificatoria suele usarse el Análisis discriminante. También para el uso de una u otra técnica juegan cuestiones de tradición, culturales. Por ejemplo, en Medicina es más usual la Regresión logística por tradición y por el papel tan destacado que en ese campo juega la Odds ratio. Sin embargo, en ámbitos como la Biología, la Ecología, la Sociología y otros es más habitual el uso del Análisis discriminante.

1. El Análsis clúster (AC), también llamado en ocasiones Análisis de conglomerados, se dice habitualmente que es una técnica estadística clasificadora, pero, en realidad, es una técnica que, como el Análisis de componentes principales (ACP) o como el Análisis factorial (AF), pretende representar una realidad que no conseguimos visualizar, una realidad cuya representación original es multidimensional y es imposible que la podamos ver en su estado puro.

2. En el fondo tanto ACP, como AF, como AC son técnicas que tratan de representan una nube de puntos original situada en un espacio de tantas dimensiones que es imposible visualizar. Y cada una de ellas, también, en el fondo, puede ser usada como método clasificatorio, como método para crear subpoblaciones, subgrupos.

3. La diferencia fundamental entre ellas es la forma de presentación que utilizan, la forma de resolver el problema de no visualización de la nube de puntos originales. El ACP y el AF lo hacen construyendo una nube de puntos de la misma naturaleza pero de menor número de dimensiones  perdiendo una parte de la información original. Sin embargo, el AC lo que hace es crear una representación distinta a la de la nube de puntos. Crea otro tipo de representación. Cambia la forma: no lo hace mediante una nube de puntos, lo hace mediante un dendrograma.

4. Cada una de las opciones tiene sus ventajas y sus desventajas, como iremos viendo a continuación.

5. El ACP y el AF respetan el tipo de representación: una nube de puntos, pero al reducir dimensiones se pierde información y esto es un problema, especialmente si la pérdida es importante. El AC respeta la nube de puntos original, no reduce dimensiones y, por lo tanto, no se pierde información, pero, eso sí, se cambia el mecanismo de representación, se cambia el estilo de representación. Representamos la nube de puntos mediante un dendrograma. Digamos que en el ACP y el AF se hace una representación figurativa y en el AC se hace una representación abstracta. Veamos un gráfico que nos ilustra la comparación:

6. A la izquierda de este gráfico tenemos una supuesta nube de puntos original. En este caso con tres dimensiones para que lo visualicemos, pero normalmente esta nube de puntos no la veremos, será una nube de puntos de muchas más dimensiones. A la derecha vemos las dos estrategias gráficas: Arriba una representación mediante una nube de puntos también, aunque en dos dimensiones que pueden ser las diseñadas por dos componentes principales o por dos factores, según la técnica utilizada. Abajo una representación bien distinta: un dendrograma, que, como a continuación veremos, se construye a partir de la nube de puntos original mediante unos procedimientos que conviene explicar con detalle.

7. Visto así parecería que el AC tiene ventajas: cambiamos la forma de representación pero no perdemos información. Parece mejor opción, pero sólo lo parece. Porque ahora veremos que en el AC hay dos momentos de decisión en la técnica que nos lleva a procedimientos que nos pueden generar realmente representaciones muy diferentes.

8. Veamos el procedo seguido por el AC para construir un dendrograma a partir de una nube de puntos original constituida por una serie de individuos de los que tienes los valores de varias variables.

9. El primer momento en el AC es definir una noción de distancia entre puntos. Necesitamos elegir una distancia, una medida que nos cuantifique distancias entre los individuos dentro de la nube de puntos original. Y aquí aparece de repente el primer problema del AC: que hay muchas distancias propuestas.

10. Ejemplos de distancias: La distancia euclídea es la más intuitiva y la más utilizada, de largo. Es la que calcula la distancia en línea recta entre los puntos en el espacio o en el hiperespacio de la nube de puntos original. Esta distancia en realidad es una aplicación del Teorema de Pitágoras:

Otra distancia muy utilizada es la denominada distancia Ciudad, que también se la llama distancia Taxi:

Otra distancia utilizada frecuentemente es la denominada distancia del máximo:

11. Veamos una comparación entre estas tres distancias:

El círculo en la métrica, el rombo en la distancia taxi y el cuadrado en la distancia del máximo delimitan puntos que están a una distanacia Épsilon del centro.

Se pueden superponer y ver cómo asignan valores diferentes de distancia a un mismo punto, o, por el contrario, asignan la misma distancia a puntos que no ocupan la misma posición; o sea, que no tienen las mismas coordenadas:

12. La distancia Mahalanobis es una distancia de mucho prestigio en Estadística Se trata de una distancia que tiene en cuenta no sólo las distancias que hay en cada una de las variables sino que cada una de estas distancias la relativiza respecto a la dispersión que tiene cada una de esas variables originales:

13. Hay muchas más distancias definidas y utilizadas. De hecho, para ser distancia una función debe cumplir las siguientes propiedades:

14. Veamos un ejemplo, en miniatura, para ver así qué pasos se siguen a la hora de hacer un AC. Vamos a ver un caso con sólo dos variables para visualizar con detalle microscópicamente todo lo que se hace, pero pensemos que lo que diga es perfectamente extrapolable al número de variables que sean. Supongamos los siguientes cinco individuos: a, b, c, d y e:

15. Vamos a construir, paso a paso, el dendrograma. Lo primero es elegir una distancia, como ya hemos dicho. Una vez elegida calcularíamos todas las distancias entre los puntos mediante esa distancia elegida. Obtendríamos, así, una matriz de distancias. Una matriz de distancias es una matriz cuadrada, simétrica y con la diagonal principal con ceros. Un ejemplo, en nuestro caso, sería la siguiente matriz:

15. La primera agrupación de puntos se hace en base a la matriz de distancias. Se agrupan los dos puntos diferentes de distancia menor. En nuestro caso serían los puntos a y b:

17. Y, por lo tanto, realizamos la primera unión en el dendrograma, la unión entre a y b.

18. A continuación nos encontramos con un problema. Ahora tenemos, en realidad, cuatro entidades para medir distancias y continuar, pero el problema es que ahora tenemos que una de esas entidades, y así será ya continuamente, son un grupo de individuos. Por lo tanto, debemos definir cómo calcularemos la distancia entre un punto y un grupo de puntos que sea, también, un criterio que nos sirva para establecer la distancia entre dos grupos de puntos, porque esto también nos aparecerá a la que tengamos en un análisis un mínimo de dos grupos.

19. Se han establecido diferentes criterios para definir la distancia entre un punto y un grupo o la distancia entre dos grupos. Veamos tres ejemplos de esos criterios: 1) El criterio del mínimo. 2) El criterio del máximo. 3) El criterio de la media. Veamos un gráfico que ejemplifica en nuestro caso cómo calcularíamos estos tres criterios:

20. Según apliquemos un criterio u otro nos podemos a encontrar con agrupaciones diferentes. Si aplicamos uno de estos criterios, por ejemplo el de la media, nos encontraríamos que, en nuestro ejemplo, la distancia menor es la que hay entre los puntos d y e:

21. Y, si continuamos con el mismo procedimiento, ahora la distancia menor entre las tres entidades que nos quedan (el grupo (a, b), el grupo (d, e) y el punto c) será la que hay entre el grupo (d, e) y el punto c:

22. Y, finalmente ya, lo último es agrupar lo que queda:

23. Y tenemos, así, el dendrograma completo. Este es el procedimiento que sigue un software estadístico para construir el dendrograma, que es la forma de representación que persigue el Análisis clúster.

24. Pero observemos cómo hemos tenido que establecer dos decisiones claves que cambian el transcurso del proceso: La distancia con la que trabajar y el criterio de cálculo de distancia entre punto y grupo o entre grupo y grupo. Y según sea la elección el resultado puede cambiar, las agrupaciones pueden ser distintas. Es cierto que si las cosas son muy claras los resultados son prácticamente los mismos, sigamos el procedimiento que sigamos, pero no siempre sucede así.

25. Una opción que suele ser también interesante es hacer el Análisis clúster girando la matriz de datos; o sea, viendo las variables como individuos y los individuos como variables. Entonces agrupamos no individuos sino variables. Vemos la proximidad de unas respecto a otras, qué agrupaciones tendría sentido hacer, etc.

26. De hecho, si hacemos un AC, de una matriz de datos, primero con los individuos y luego con las variables, estamos cubriendo aquellas dos finalidades que persiguen tanto el ACP como el AF, que son: 1) Representar los puntos, visualizarlos. 2) Ver relaciones entre las variables, agrupaciones, conexiones entre ellas.

27. Veamos la aplicación del AC a los datos de los estudiantes que hemos visto en los temas dedicados al ACP y al AF. Al aplicar a los 15 alumnos para todas las variables; o sea, a la nube de puntos original, el AC con la distancia euclídea y el criterio de distancia entre punto y grupo o entre grupo y grupo el de la media del grupo, el dendrograma que se construye es el siguiente:

28. Si hacemos lo mismo pero ahora con las variables obtenemos el siguiente dendrograma:

29. Lo que muestra realmente lo que decíamos de la agrupación que se produce entre variables: Letras por un lado y Ciencias por otro. Aquí Educación acaba agrupándose primero con las ciencias que con las letras, pero es la última agrupación, si quisiéramos crear tres grupos de variables y cortáramos el dendrograma a nivel de obtención de tres grupos de variables tendríamos: Letras, Ciencias y Educación física.

30. Es interesante comparar los resultados obtenidos, las representaciones dibujadas, con las tres técnicas: ACP, AF y AC a los mismos datos. Al final tenemos, como ya hemos dicho, dos formas muy distintas de hacer lo misma: la del ACP y AF, por un lado, y la del AC, por otro. Dos formas de representación muy distinta. Pero la finalidad fundamental de ambas es descriptiva: representar lo que no podemos visualizar en su estado original, hacer una representación aproximada, crear un modelo de aquella realidad que no tenemos. Y junto ahora las dos formas tan distintas de hacer lo mismo en un mismo gráfico. Pongo sólo el AF en representación de la opción generada por AF o por ACP:

31. Lo primero que vemos si comparamos ambos gráficos es que son dos representaciones muy distintas: como cuando vemos un cuadro de Picasso o de Velazquez. A lo mejor los dos intentan pintar lo mismo: las meninas, por ejemplo, pero lo hacen mediante técnicas pictóricas bien distintas. Una figurativa, la otra más abstracta. Pero con un poco de paciencia pueden irse estableciendo paralelismos entre ambos gráficos igual que con las merinas de Velazaquez y de Picasso.

32. El 5 y el 11 forman un grupo: son los alumnos que son buenos tanto en ciencias como en letras. El 2, 7, 4, 10 y 13 forman otro grupo: son los alumnos buenos en letras pero malos en ciencias. El 6 y 8 otro grupo: son los alumnos buenos en ciencias pero malos en letras. El 12 y 14: el grupo de los malos en ciencias y en letras. Finalmente, hay un grupo formado por el 1, 15, 3 y 9 que están en medio, que les va todo justo, están en la frontera entre el aprobado y el suspenso tanto en ciencias como en letras. Veámoslo en el siguiente gráfico que es el mismo de antes pero con estos grupos marcados tanto en una como en la otra representación:

32. Como puede verse estamos haciendo cosas similares aunque a través de procedimentos bien distintos.

1. El punto de partida del Análisis factorial (AF) es el mismo que el del Análisis de componentes principales (ACP). De hecho, como explicaré más adelante, en realidad, el ACP es un AF que, debido a su simplicidad y su aplicabilidad, se ha independizado y ha adquirido vida propia. Hemos visto primero el ACP porque es más sencillo en cuanto a maquinaria y, por razones, didácticas es mejor empezar por él.

2. La finalidades del AF son, pues, las mismas que teníamos en el ACP: 1) Conseguir una representación gráfica de una realidad que es imposible representar en toda su extensión, visualizar una visión aproximada de una nube de puntos original que es imposible visualizar por exceso de dimensiones. 2) Conseguir combinaciones de las variables originales que nos ayuden a discernir tipos de relaciones que se establecen entre las variables del estudio.

3. Recordemos, en primer lugar, en formato matemático, cuál era el procedimiento del ACP. Se trataba de crear unas nuevas variable (la componentes) que tuvieran una gran diferencia entre la variabilidad explicada y que, cada una de ellas fuera combinación lineal de las variables originales:

4. De d variables originales obtenemos d componentes, pero nos quedamos únicamente con las primeras, las principales, por almacenar en su interior mucha más información de la nube de puntos original. El formato matemático del AF es este otro:

5. A las variables F₁, F₂, …, F_c, las llamamos factores. Importante que c sea menor que d. En realidad, interesa que sea mucho menor, que con dos o tres factores tengamos suficiente, como con la componentes principales: interesa que unas pocas acumulen mucha información, mucha varianza de la nube de puntos original. Cada uno de los factores es, también, como las componentes, una combinación lineal de todas las variables originales:

6. Como puede apreciarse estos factores son como las componentes. Los factores son independientes entre ellos, también, como las componentes. Pero no se crean d factores sino que se crean un número c que es siempre menor que d, como ya hemos dicho antes.

7. El conjunto de estos factores constituyen la llamada comunalidad. Esto es muy interesante. Observemos aquí la diferencia con el planteamiento del ACP. En el AF escribimos cada una de las variables originales como una combinación de esos factores comunes. Los factores son, por lo tanto, elementos que están en el interior de esas variables, como sus elementos indisociables. Los factores son como si fueran las piezas profundas de lo que está hecha la diversidad de las variables que vemos y cuantificamos. Los factores serían, pues, como los átomos que se combinan, en proporciones distintas, en las moléculas (que serían las variables del estudio).

8. Las variables U₁, U₂, …, U_d son las llamadas unicidades, porque cada una de ellas es única y distinta en cada una de las variables originales. La comunalidad capta lo común, las unicidades suman lo diverso.

9. Las unicidades son una especie de Residuo, un elemento individual de cada una de las d variables originales y que es lo que queda por explicar de cada una de ellas después de haber sumado una combinación peculiar y única de los factores en cada una de ellas, después de haber introducido en ellas lo que tienen de la comunalidad, de lo común, de lo que se explica por los factores comunes elegidos.

10. Es muy importante comparar el AF con el ACP, porque en esa comparación está el elemento diferencial entre esas dos técnicas y será precisamente esta comparación la que nos ayudará a encontrar la singularidad del Análisis que ahora nos ocupa.

11. Lo primero a distinguir es que en el ACP tiene solución única, lo que significa que, cuando se pone en marcha la maquinaria de la técnica frente a unos datos, hay una única solución, la que proporciona, como hemos visto, los valores propios y los vectores propios. La única opcionalidad que tenemos es, como ya hemos dicho en el tema dedicada al ACP, trabajar con la matriz de correlaciones o la de varianzas-covarianzas. Sin embargo, en el AF, no hay una única solución, hay distintas formas de extracción de los factores y cada una de ellas da lugar a un resultado distinto. Al separar una parte común (la comunalidad: los factores) y una parte única (las unicidades) de cada una de las variables originales, estamos creando las condiciones para generar formas distintas de llegar a esa situación y, por lo tanto, que haya soluciones distintas.

12. Al no haber una solución única, como sucede con el ACP, se han diseñado muchas formas de extracción de los factores. Posiblemente el sistema de extracción de los mínimos cuadrados sea el más usual, pero hay otros, por ejemplo: Método del centroide, Método de Jacobi, Método de la máxima verosimilitud. De hecho, el propio sistema de las componentes principales es también un método de extracción de factores: mediante ese método se seleccionan las dos o tres primeras componentes conviertiéndolas en los factores. Observemos que entonces las componentes Y las convertimos en factores F. Hay que decir que, aunque sean muchos los métodos de extracción, en realidad son pocos los que han sido implementados en los principales software estadísticos.

13. El sistema de los mínimos cuadrados, que es uno de los métodos más usado, se basa en la búsqueda de la recta, del plano o del hiperplano (dependiendo del número de factores elegidos) que minimice las unicidades, que actuarían aquí como el residuo de la Regresión. Es un planteamiento derivado, evidentemente, de la Regresión lineal.

14. Gráficamente esto que estoy diciendo se puede ilustrar de la siguiente forma: Dada una nube de puntos según el criterio que sigamos puede ser que el factor generado sea ligeramente diferentes. Por ejemplo, en el siguiente caso la recta roja podría seguir el criterio de las componentes (la búsqueda de la máxima variabilidad en el primer eje) y la recta verde podría seguir el criterio de los mínimos cuadrados:

15. La segunda diferencia entre el ACP y el AF está en la idea de rotaciones presente en el AF y que no lo está en el ACP. Una vez se han extraído los factores, cada uno de ellos es, como hemos visto, una determinada combinación de las variables originales, combinación caracterizada por una serie de coeficientes que multiplican a esas variables y que están asociados a cada factor. Pues bien, esos factores se pueden rotar según criterios distintos. Se trata de pequeños giros de los nuevos ejes de coordenadas con la finalidad de mejorar algún aspecto prefijado.

16. Rotar implica que cambien los coeficientes. Cualquier cambio de los ejes supone un cambio de los coeficientes. Si con ligeros cambios de los ejes, y, por lo tanto, de los coeficientes, se pierde poca capacidad de representación y se gana en algún criterio prefijado, entonces vale la pena la rotación.

17. El método de rotación más usual es el Varimax que minimiza el número de variables, en cada factor, con coeficientes elevados en valor absoluto.

18. Pensemos que el juego de muchos coeficientes actuando en un factor, en el AF, o en una componente principal, en el ACP, puede dificultar mucho su interpretación. Es difícil ponerle  entonces nombre a esa macrovariable. La rotación Varimax realiza una rotación que simplifica, lo más posible, el repertorio de coeficientes. Se consigue que haya menos coeficientes con valores absolutos grandes pero que esos valores absolutos sean más grandes que sin la rotación. Esto aclara la interpretación, generalmente.

19. Existen otros criterios de rotación: Quartimax, Equamax, etc, pero son de largo mucho menos utilizados que el Varimax. Evidentemente la rotación es una opción, no una obligación. Puede hacerse un Análsis factorial sin rotación.

20. Por lo tanto, ante un AF debe decidirse el método de extracción y, luego, si se hace o no rotación. Si se hace rotación debe decidirse con qué criterio, con qué método de rotación.

21. Visto todo esto podemos situar ahora el ACP como un AF especial, tan especial que ha conseguido independizarse, como ya hemos dicho antes. El ACP es un AF al que se le aplica como método de extracción el de las componentes principales y al que no se le aplica ninguna rotación.

22. Vamos a aplicar el AF a los datos de las notas de 15 estudiantes en ocho materias diferentes que usamos para aplicar el ACP. Recordemos la matriz de datos:

23. Si aplicamos el método de extracción de los mínimos cuadrados y la rotación varimax conseguimos los siguientes valores propios de la matriz de correlaciones:

23. Con dos factores explicamos, por lo tanto, el 95.56 de la varianza. La comunalidad es la siguiente:

24. Esto significa que los dos factores seleccionados explican estos tantos por uno de estas variables originales. Son todos muy altos (suele entenderse por alto a partir de 0.75 ó 0.8). El único que no llega a este nivel es la variable Educación física. Se trata de una variable que si le sumamos los factores combinados de alguna forma sólo conseguimos explicar el 47.12% de su medida, por lo tanto, tiene una elevadísima unicidad no contemplada en los factores. Esto ya lo veíamos en el ACP: la Educación física va un poco por libre, mide un tipo de cosas que no tiene relación con lo que miden las otras materias.

25. El número de factores elegidos será el resultado de valorar dos cosas: 1) Que mediante ellos obtengamos un porcentaje de explicación como mínimo del 75-80% y esto lo veremos mediante los valores propios. 2) Que la comunalidad de las variables originales, o al menos del grupo de ellas que especialmente queremos explicar, sea también, al menos del 75-80%, o de 0.75-0.8, en tanto por uno.

26. Y a continuación vamos a ver cuáles son las fórmulas de los dos factores con la rotación varimax:

27. Como puede verse el primer factor recoge como coeficientes grandes las materias de letras: Lengua, Inglés Filosofía e Historia. El segundo factor recogen como coeficientes grandes las materias de ciencias: Matemáticas, Física y Química. Como sucedía en el ACP.

28. El gráfico de los 15 alumnos representados respecto a los dos factores elegidos es:

29. Realmente si lo comparamos con el obtenido mediante el Análisis de componentes principales es muy similar. Recordemos aquél gráfico:

30. Comparando ambas técnicas, el AF y el ACP, aplicadas a los mismos datos podemos comprobar que los resultados obtenidos son similares. Los dos factores y las dos componentes principales se interpretan de la misma forma. Las representaciones son prácticamente idénticas. Son dos formas distintas de llegar al mismo sitio, por lo tanto. En este ejemplo, las cosas son muy claras y de ahí la similaridad. La varianza explicada en ambos caso es muy alta lo que favorece la igualdad en los resultados. Si no fuera tan alta esta varianza total explicada podríamos encontrarnos con mayores diferencias.

31. El ejemplo que hemos utilizado es sencillo. Con datos complejos, donde el repertorio de variables es amplio y diverso suele ser muy difícil interpretar el ACP. Especialmente en estos casos el AF puede aportar una luz que no seamos capaces de ver mediante el ACP.

32. Por otra parte, mucha diferencia en las representaciones obtenidas por un método u otro no deben existir, porque, en realidad, estamos intentando, como ya hemos dicho, con ambas técnicas, representar una nube de puntos original, que no visualizamos, mediante una nube de puntos en menos dimensiones. Si un método de este tipo cumple su misión debe llegar a una solución similar a la obtenida por otro método diferente que persigue lo mismo. Únicamente en los casos en los que estemos haciendo representaciones muy poco fieles a la original podemos encontrar profundas diferencias entre estos distintos métodos.

Toda la explicación que a continuación tenéis del Análisis de componentes principales la podéis seguir, también, paralalamente, con la explicación de los siguientes vídeos:

 

1. El Análisis de componentes principales (ACP) es una técnica estadística descriptiva que tiene como punto de partida una matriz de datos con una serie de individuos a los que se les ha medido varias variables. Por eso suele clasificarse como una técnica multivariante. Para guiarnos en esta técnica vamos a manejar unos datos como los que a continuación muestro:

2. Se trata de unos datos que todos comprendemos perfectamente porque todos hemos sido estudiantes. Se trata de las notas de diferentes materias que obtienen 15 alumnos de bachillerato. Tenemos, pues, 15 individuos en el estudio; o sea, una muestra de tamaño 15 pero con ocho variables, tantas como asignaturas tenemos.

3. Si quisiéramos representar los 15 alumnos de esta muestra en un gráfico lo podríamos hacer tomando dos notas y representando los 15 puntos según sus valores en el eje de abscisas y de ordenadas. Podríamos también, eso sí, hacer una representación de tres de esas ocho variables en un gráfico tridimensional. Pero aquí se acaba. Ya no podríamos visualizar una representación en más dimensiones. Por lo tanto, es imposible ver en un gráfico una representación de los 15 individuos respecto a todas las variables al mismo tiempo.

4. El ACP tiene como objetivo básico inicial suplir este déficit. Pretende, cuando vale la pena hacerlo (ya veremos cuándo vale la pena y cuándo no), realizar una representación de una nube de puntos multidimensional (de más de tres dimensiones), en dos o tres dimensiones. En definitiva, se trata de visualizar lo que no vemos. En nuestro ejemplo de los estudiantes de bachillerato el ACP trataría de hacer una representación de los 15 alumnos en dos o tres dimensiones pero contemplando todas las variables, sin prescindir de ninguna de ellas en el análisis.

5.  Hay que hacer notar que, aunque el objetivo inicial es éste: la representación en dos o tres dimensiones de unos puntos que originariamente están en muchas dimensiones; o sea, visualizar lo que no vemos, la propia técnica, como consecuencia de su propio procedimiento, consigue crear unos objetos matemáticos (las componentes) muy interesantes que, en realidad, también podrían considerarse objetivos de la técnica porque, en muchas ocasiones, nos permiten establecer relaciones entre las variables, ver cómo se asocian, cómo se distancian, etc. De esto, no obstante, hablaré más tarde.

6. Vamos a ver el problema que estoy planteando pero miniaturizado. Así se entenderá mejor la esencia de la técnica. Supongamos que tenemos la siguiente representación bidimensional con dos variables X₁ y X₂:

7. Y supongamos que unos seres unidimensionales, que únicamente ven las cosas si están en una dimensión, quieren representar, en una única dimensión, esta nube de puntos que ellos, evidentemente, no pueden ver. Observemos que si lo que quieren es no prescindir de ninguna de las dos variables lo que pueden hacer es representar las proyecciones de los puntos sobre un eje como el dibujado en la siguiente figura:

8. Observemos que la nube de puntos roja, que está integrada por las proyecciones de los puntos originales sobre el nuevo eje, se parece bastante a la nube de puntos original. Las posiciones relativas de los puntos se respetan bastante. Y ahora los seres que sólo ven en una dimensión lo ven. Están viendo una representación unidimensional de una realidad bidimensional y lo hacen con bastante fidelidad. La nube de puntos roja se parece bastante a la negra. Ellos sólo ven la roja pero realmente es una buena aproximación de la original, que es la negra.

9. La representación en menos dimensiones no siempre tiene la misma calidad. En el gráfico siguiente vemos que a la izquierda la nube de puntos proyectada sobre el nuevo eje (la nube de puntos roja) se parece más a la original de lo que se parecen la roja y la negra en la situación mostrada en el gráfico de la derecha. Por lo tanto, en los datos de la derecha tiene menos valor realizar un ACP:

10. Y observemos que cuando he dibujado el eje para proyectar los valores sobre él lo he hecho situándolo de una forma, pero lo hubiera podido situar de otra. Observemos en el gráfico siguiente que el eje dispuesto en el ejemplo de la derecha no consigue, mediante la proyección de los puntos sobre ella, una nube de puntos representativa de la nube de puntos original:

11. Lo que hemos hecho es, en definitiva, un giro de los ejes de coordenadas sin tocar los puntos. Observemos lo que hemos hecho:

12. Lo importante es que ahora vemos la nube de puntos desde unos ejes donde uno es mucho más importante que el otro. Ahora los ejes son Y₁ y Y_2. Si X₁ y X₂  eran dos variables que tenían la misma cantidad de información, ahora Y₁ y Y₂ no tienen la misma cantidad de información. Y₁ tiene mucha más información que Y_2. En Estadística información es equivalente a dispersión, a varianza. Una variable que no varía no tiene información. Una variable que varía mucho tener el valor de un individuo es muy informativo.

13. El objetivo de la técnica ACP es, pues, éste: conseguir girar los ejes de tal forma que exista la mayor desigualdad posible entre la varianza de la nube de puntos original en las proyecciones en cada uno de los respectivos nuevos ejes y que, además, estos ejes, estas nuevas variables, sean independientes entre sí; o sea, que tengan correlación cero.

14. La búsqueda de estos nuevos ejes se hace mediante el cálculo de los llamados valores propios y vectores propios de la matriz de correlaciones entre todas las variables del estudio. Puede hacerse también a partir de otra matriz, la de varianzas-covarianzas, pero ésta tiene el problema de que cuando las variables tienen unidades de escala muy diferentes introduce un exceso de influencia por parte de las variables con mayor varianza. Por esto suele trabajarse con la matriz de correlaciones. De esta forma se unifica el peso de las variables iniciales del estudio. Suele hablarse de variables estandarizadas cuando se trabaja con la matriz de correlaciones. Una variable es estandarizada cuando la muestra se transforma a media cero y Desviación estándar uno. Esto se hace restando a cada valor muestral la media muestral y dividiendo por la Desviación estándar. De esta forma todas las variables del estudio tienen la misma media y la misma Desviación estándar y ninguna pesa más que otra. De esta forma la vocalización del estudio se pone en cómo es la forma de la nube de puntos, de cuáles son las relaciones entre las variables que permiten reducir dimensiones perdiendo el mínimo de información.

15. Algo muy importante: ¿Cuál es la relación existente entre las variables originales y las nuevas variables, los nuevos ejes; o sea, cuál es la relación, en el caso que hemos dibujado entre las variables X₁ y X₂  y las variables Y₁ y Y_2?

16. En primer lugar decir que a las variables Y₁ y Y₂, que son, eso, variables, también, como las originales, las llamamos en esta técnica “Componentes”. Y son cada una de ellas una combinación de las variables originales. Observemos la fórmula de esa combinación:

17. En realidad estos coeficientes que multiplican a las variables originales son los vectores propios de la matriz de correlaciones, es la fórmula de la transformación lineal realizada. Hemos cambiado de ejes y para llegar de los ejes originales a los nuevos ejes hace falta esta transformación. En definitiva, si tenemos un punto representado por las coordenadas originales, éstas son las fórmulas necesarias para conseguir las coordenadas de la nueva representación: la representación mediante los ejes constituidos por las componentes.

18. Si en el lugar de estar trabajando con dos variables originales estuviéramos trabajando con d variables originales la fórmula de las d componentes sería:

19. Se llama a la técnica Análisis de componentes principales porque transforma a las variables originales en nuevas variables, las componentes, las cuales tiene desigualdad en cuanto a la información explicada, lo que significa que tenemos unas componentes muy informativas y otras que no. Por eso tenemos unas componentes principales, que son las que usaremos para hacer la representación. Esta desigualdad generada al crear las componentes nos permite elegir, entre ellas, las principales y eliminar las poco importantes, cosa que no sucedía con las originales porque ellas eran todas principales, todas eran importantes, no podíamos prescindir de ninguna de ellas.

20. A los datos de los 15 estudiantes que se les ha evaluado en las ocho materias citadas en la matriz de datos mostrada al principio de este tema si se les hace un ACP tenemos la siguiente representación usando las dos primeras componentes principales: PCOMP_1 y PCOMP_2:

21. Observemos ahora que esta representación se asemeja mucho a la original en ocho dimensiones. Si observamos en el gráfico de dos dimensiones el alumno 1 y el 9 están muy próximos, prácticamente solapados. Miremos qué sucede en la matriz de datos. Observaremos que las notas, excepto Educación física, son prácticamente las mismas. Lo de Educación física tiene una explicación que ahora veremos.

22. Si, por el contrario, elegimos los individuos 5 y 12 vemos que en nuestro gráfico de dos dimensiones están completamente en los extremos, están en dos vértices de la representación. Si ahora miramos la matriz de datos veremos que el alumno 5 lo aprueba todo con buenas notas excepto la Educación física. En cambio el alumno 12 lo suspende todo, incluso la Educación física. Sorprendentemente en este caso son en todo distintos excepto en la Educación física que tienen justo la misma nota.

23. Por lo tanto, con el gráfico de dos dimensiones estamos viendo una muy buena fotografía de las posiciones relativas de los puntos en la representación de ocho dimensiones original que no vemos. Digo fotografía porque la metáfora es apropiada. Pensemos que cuando estamos viendo una fotografía en realidad estamos viendo una representación bidimensional de una realidad tridimensional. En el ACP estamos haciendo algo similar. Miramos de hacer una fotografía bidimensional o tridimensional, para que la podamos visualizar, de una realidad constituida por muchas dimensiones y que no visualizamos. Por lo tanto, en nuestro caso estamos viendo una fotografía bidimensional de una realidad ochodimensional.

24. Pero, algo muy importante: ¿Qué cantidad de información perdemos? Y, ¿qué representan los nuevos ejes?

25. Respecto a la cantidad de información observemos la siguiente tabla:

26. Los valores propios de cada componentes nos indican la cantidad de varianza, la cantidad de información que tiene cada componente. Como podemos ver en esta tabla la primera componente tiene un 46.38% de información y la segunda un 35.76%. Las dos juntas tienen un 82.14. Por lo tanto, haciendo una representación en dos dimensiones con esas dos primeras componentes perdemos un 17.86% de información únicamente.

27. Respecto a lo que representan los nuevos ejes observemos la fórmula de las dos primeras componentes principales:

28. Esto indica que la primera componente principal tiene los coeficientes de la primera columna y la segunda componente tiene los coeficientes de la segunda. O sea, que para conocer las coordenadas que tendrá cada alumno de esas dos componentes hay que multiplicar sus ocho notas por sus coeficientes respectivos. Y así es como obtenemos la representación gráfica bidimensional mostrada antes.

29. Para interpretar una componente hay que seguir el siguiente procedimiento: 1) Mirar el valor absoluto de los coeficientes distinguiendo los que tienen un valor grande y un valor pequeño. En nuestro caso en la primera componente observemos que Lengua, Inglés, Filosofía e Historia tienen coeficientes con valor absoluto grande, cercano en todos los casos a 0.5. Los demás ya son bastante más pequeños, pesan mucho menos en esta componente. En la segunda componente el peso principal se lo llevan Matemáticas, Física y Química, con coeficientes cercanos a 0.57. Las demás asignaturas pesan poco. 2) Mirar entre los coeficientes con valor absoluto grande el juego de signos que hay. En nuestro caso el signo es el mismo, por lo tanto, las variables que pesan en una componente y en la otra todas van en la misma dirección. Pero en otro caso nos podríamos encontrar con valores de signo contrario. Entonces hay que interpretar el juego de fuerzas de los signos.

30. En el ejemplo que venimos usando la interpretación es muy clara. En la primera componente tenemos reunidas las materias de letras. En la segunda componente tenemos reunidas, por el contrario, las materias de ciencias. La educación física no pesa ni en una ni en otra. Porque no tiene ninguna relación ni con las materias de letras ni con las de ciencias.

31. Viendo el gráfico bidimensional donde en el eje de las abscisas tenemos la primera componente y en el eje de las ordenadas tenemos la segunda componente podemos ver que los alumnos buenos en ciencias y letras estarán situados a la derecha y arriba, los alumnos buenos en letras y malos en ciencias se situarán a la derecha y abajo, los buenos en ciencias y malos en letras a la izquierda y arriba y, finalmente, los malos en ciencias y letras se situarán a la izquierda y abajo.

32. Veamos otro ejemplo de ACP. La matriz de datos son variables meteorológicas según comarcas catalanas el año 2005. Los datos son los siguientes:

33. Al hacer un ACP, los valores propios de las componentes principales son los siguientes:

34. Como puede verse con las dos primeras componentes explicamos el 77.41% de la varianza, de la información contenida en la nube de puntos original.

35. Y los vectores propios; o sea, los coeficientes de las dos primeras componentes, son los siguientes valores:

36. En la primera componente pesan; o sea, tiene valor absoluto grande, las tres variables de temperatura y la altitud media de la comarca. Además lo hacen las temperaturas con signo positivo y la altitud con signo negativo. Lo que indica que valores grandes de la primera componente corresponden a comarcas con temperaturas altas y altitud baja. Altitud baja porque como el coeficiente es negativo para que la componente tenga un valor alto hace falta que la altitud reste poco, sea un valor pequeño. Contrariamente, valores pequeños de esta primera componente indica temperaturas bajas y altitud alta.

37. En la segunda componente pesan especialmente las variables Precipitaciones, Humedad y Velocidad del viento. Las dos primeras con signo positivo y la tercera con signo negativo. Valores grandes de esta componente indicarán zonas con mucha lluvia, mucha humedad y poco viento. Por el contrario, valores bajos de esta segunda componente corresponderán a comarcas de bajas precipitaciones, baja humedad y alta velocidad del viento.

38. La representación de las comarcas según las dos primeras componentes es la siguiente:

39. Viendo el gráfico y la anterior interpretación de las componentes podemos dividir el gráfico en cuatro cuadrantes y afirmar: 1) Arriba a la derecha: Comarcas calurosas y húmedas. 2) Abajo a la derecha: Comarcas calurosas y secas. 3) Arriba a la izquierda: Comarcas frías y húmedas. 4) Abajo a la izquierda: Comarcas frías y secas.

40. Observemos, pues, que conseguimos con esta técnica representar en pocas dimensiones una realidad multidimensional y, también, crear estas componentes, estas variables de variables, variables que son combinación de las variables originales. Y estas combinaciones son interesantes en sí mismas, porque nos ayudan a crear una especie de conglomerados de variables combinadas de una forma que, en realidad, reflejan la vida interna que tienen ellas entre sí en cuanto a la covariación conjunta.

41. En el primer ejemplo, el caso de las notas, las componentes nos han creado la noción de Letras y la noción de Ciencias, reflejando una idea que todos tenemos en mente: que las capacidades hacia un ámbito u otro son como dos dimensiones independientes que se pueden tener ambas, que se puede tener una y no otra o que se puede, también, no tener ninguna.

42. En el segundo ejemplo, las componentes nos separan dos elementos independientes: aspectos de frío o calor, ligados a la altitud de la zona, por un lado, y aspectos referentes a la humedad climática, por otro. Aspectos que pueden ir asociados entre sí de forma independiente creando cuatro tipos de comarcas o de zonas distintas según la combinación de los valores extremos de estas dos componentes.

43. Otro ejemplo de Análisis de componentes aplicado a datos de jugadores de baloncesto se puede consultar en el fichero Análisis de componentes principales aplicado a datos de jugadores de baloncesto.

44. Otro ejemplo interesante es el planteado en la Situación 66, donde aparecen unos datos de diferentes países y las proporciones que tienen que hay en ellos en cuanto a las distintas formaciones universitarias. El análisis de los datos los podéis ver en la Solución Situación 66.

45. Otro ejemplo, ahora con Pokémons, está planteado en la Situación 47. La solución se puede ver en el fichero Solución Situación 47.

46. Un ejemplo de fútbol lo tenemos en la Situación 46. La solución puede verse en el fichero Solución Situación 46.

47. Como puede verse, en este tema hemos hablado de una técnica esencialmente descriptiva. No hemos hablado, aquí, de otra cosa que de muestras. No hay voluntad inferencial en esta técnica. Es cierto que se ha estudiado y creado técnicas inferenciales relacionadas con el ACP pero no es muy utilizada en la práctica. Es por ello que debemos considerarla una técnica descriptiva, una técnica que intenta buscar la representación de una muestra de individuos de los que tenemos muchas variables de interés. Una técnica donde la muestra es la finalidad.

48. Podéis practicar los conceptos de este tema con ejercicios comentados en el siguiente:

 

1. La pregunta que más se le hace a un estadístico es: «¿Qué tamaño de muestra necesito?».

2. El problema que tiene esta pregunta es que, así, sin más, no tiene respuesta. Es una pregunta que engendra preguntas porque el estadístico, sin más información, no puede decir nada, como veremos a continuación.

3. Es conveniente diferenciar dos ámbitos distintos en la determinación del tamaño de muestra: a) Cuando hacemos una predicción. b) Cuando hacemos un contraste de hipótesis. Empezaremos planteando el primer caso y, en concreto, ejemplificado en la predicción de una media poblacional.

4. El radio (r) de un intervalo de confianza de la predicción de la media poblacional, la Desviación estándar (DE) y el tamaño muestral (n) mantienen una relación que puede expresarse en una ecuación muy importante en Estadística:

5. Recordemos que un intervalos de confianza de la media como, por ejemplo: (5, 15), tiene como radio 5 y como diámetro tendría 10. Y recordemos, también, que estos intervalos tienen un porcentaje de confianza. Recordemos, también, que esta expresión la podemos deducir de todo lo visto en el Tema 3: Intervalos de confianza.

6. Esta constante k dependerá de ese porcentaje de confianza con el que queramos expresar el pronóstico. En el caso de que estemos trabajando con la media poblacional y en caso de seguir, nuestra variable, la distribución normal, o, si no es así, que el tamaño muestral sea grande (superior a 30) este valor de k, si el nivel de confianza es del 95%, es aproximadamente 2.

7. Por lo tanto, la ecuación quedaría así:

8. Vamos a reflexionar algunas cosas importantes que se desprenden de esta importantísima igualdad.

9. Esta ecuación no aparece por arte de magia, surge de la fundamental noción de Error estándar (EE), cuya expresión recordemos que, para el pronóstico de la media poblacional, es EE=DE/raiz(n).

10. De hecho, ya lo hemos dicho en diferentes ocasiones, que en cualquier estimación, en cualquier pronóstico, está implicado el Error estándar. El EE es una DE, pero es la DE de una predicción. Esto es lo que lo caracteriza.

11. Pero, además, hemos visto también que la noción de EE era fundamental para la construcción del intervalo de confianza del 95%.

12. Y en la ecuación r=2•DE/raiz(n) la parte derecha de la igualdad es esa expresión de dos veces el error estándar.

13. Otra forma de expresar esa ecuación, despejando la n, es:

donde ya la tenemos en la forma deseada, porque lo que queremos es determinar el tamaño de muestra, la n, en un estudio concreto.

14. Una vez tenemos la ecuación podemos hacer afirmaciones a partir de ella. En una ecuación la posición relativa de los conceptos es muy importante. Veamos: Si hay mucha dispersión necesitamos más n. Si hay poca dispersión no necesitaremos tanto tamaño de muestra. La relación entre n y la DE es directa. A más DE más n. A menos DE menos n.

15. Si necesitamos una precisión grande en nuestras predicciones; o sea, un radio r pequeño, entonces deberemos tener una muestra grande. Si no necesitamos mucha precisión; o sea, si no precisamos un radio r muy pequeño, la muestra podrá ser menor. Por lo tanto, el tamaño de muestra está relacionado de forma inversa con ese radio del intervalo.

16. O sea, a la hora de elegir un tamaño de muestra debemos saber qué precisión necesitamos y qué dispersión podemos prever que tendremos en la futura muestra. Necesitamos saber, pues, cómo será la muestra que aún no tenemos.

17. Esta paradoja es importante: para elegir un tamaño de muestra ideal necesitamos saber cómo será la dispersión de esa futura muestra.

18. El conocimiento de lo que todavía no conocemos lo debemos suplir por información de otros estudios previos o por una muestra piloto, una pequeña muestra previa, una premuestra, que nos permita hacer una previsión de la dispersión que tenemos en el estudio.

19. Respecto a la precisión requerida en el estudio, expresada ésta por el radio del intervalo (r), no siempre uno sabe lo que le interesa o lo que necesita. En este caso lo que uno quiere es estar lo más cerca del valor que estima. Pero es necesario especificar, de antemano, esa precisión porque de ello depende el tamaño de muestra que hemos de tomar. Porque está en la ecuación.

20. Un ejemplo: Estamos estudiando la media de altura de una población adulta y queremos construir un intervalo de confianza del 95% de la media poblacional cuyo radio no sea mayor que 1; o sea, queremos construir un intervalo de confianza con el valor de la media muestral más menos 1.

21. Observemos que a partir de la ecuación n=4•DE²/r² sabemos r que vale 1, pero nos falta saber DE. Si sabemos, por otros estudios, que la DE en estas poblaciones es un valor cercano a 10 ya lo tenemos todo para determinar el tamaño de muestra que necesitamos. Entonces el tamaño de muestra ideal para trabajar es: n=4*100/1=400. Con este tamaño de muestra y con esta dispersión podremos construir un intervalo de confianza del 95% de la media poblacional a partir de la media muestral que calculemos a la muestra con un radio de 1.

22. Observemos ahora lo mismo pero visto desde el otro lado: Tomamos una muestra de tamaño 400 y calculamos la media que es, por ejemplo, 170 y la DE que resulta ser, finalmente 10, como ya habíamos predicho por estudios previos. Entonces, al calcular el intervalo de confianza de la media poblacional lo haríamos sumando y restando dos veces el Error estándar. Y el Error estándar, en esta muestra, sería 10/raíz(400)=0.5. El intervalo de confianza sería, entonces, 170±1, que es del nivel de precisión que queríamos.

23. Si la variable es dicotómica (una variable como hombre-mujer o tiene o no diabetes) la fórmula es la misma pero ahora la DE es raíz cuadrada de p(1-p), que es la Desviación estándar de una variable dicotómica. O sea, debemos saber cuál debe ser, aproximadamente, el valor de p que acabaremos estimando para ponerlo en la ecuación. Ante la duda se elige como p el valor de 0.5 que nos daría el máximo valor posible de tamaño muestral. Supongamos que queremos estimar la prevalencia de la diabetes en un país y queremos determinar el tamaño de muestra. Sabemos por otros estudios que debe estar en torno al 10% (0.1 en tanto por 1). Queremos tener un radio del intervalo del 1%. Entonces la fórmula sería: n=4*0,1*0,9/0,0001=3600. El 0,0001 es por el 0,01 al cuadrado. La fórmula general en una variable dicotómica es, pues:

24. Con esto hemos visto que el tamaño de muestra n en un caso de estimación de un valor poblacional, en un caso de un pronóstico poblacional, es una función de la DE y de la precisión requerida, expresada como el radio del intervalo de confianza. Sin estos dos valores no es posible determinar el tamaño de muestra requerido; o sea, expresado en forma funcional, podemos decir que n es función de DE y de r:

25. Sorprende mucho a todo no estadístico que consulta por el tamaño de muestra que necesita (lo repito porque es muy importante que quede muy claro)  que precise de la DE antes de coger la muestra, porque es precisamente la muestra la que le acabará dando esa DE. Es aparentemente un círculo vicioso, pero es así. No hace falta tener un valor exacto pero sí aproximado de cuál será la DE con la que se encontrará. Esto puede llegar a saberlo por estudios previos equivalentes hechos por otros o mediante una muestra piloto, o premuestra.

26. Cuando el problema es determinar el tamaño de muestra en un contraste de hipótesis la situación es otra (Recordemos que en el punto 3 hemos visto que la determinación del tamaño de muestra es conveniente verla en dos ámbitos por separado). Entran en juego, ahora, muchos más elementos. En el caso, por ejemplo, de un contraste de la diferencia de medias tendríamos ahora una función de cuatro variables como la siguiente:

donde alfa es el nivel de significación, 1-beta es la potencia, DE es, como antes, la Desviación estándar y d es la diferencia mínima que interesa detectar.

27. Una función, pues, que depende de cuatro factores, de cuatro valores. Necesitamos más cosas, pues, que antes. Veámoslas una a una: La primera, la alfa, es la menos problemática, es el nivel de significación, es el error de tipo I (Ver el artículo La noción de potencia estadística), solemos fijarla siempre en el valor 0.05.

28. La 1-beta es la potencia estadística (Ver, de nuevo, también, el artículo La noción de potencia estadística). Interesa que sea un valor alto. La beta es, como se puede ver también en ese artículo citado, el denominado error de tipo II, un error que no está fijado de antemano, como sí sucede con el error de tipo I, y que, por lo tanto, conviene conocerlo, puesto que para que el procedimiento de decisión sea bueno deben ser pequeños los dos tipos de error que se pueden cometer. La potencia suele aceptarse que a partir de 0.8 es ya una potencia considerable. Lo ideal, no obstante, sería tenerla de 0.95.

29. Con la DE pasa lo de antes, necesitamos buscar información de estudios similares o tomar una premuestra para saber aproximadamente cuál es su valor.

30. La d suele ser compleja. Al estadístico es lo que le cuesta más conseguir del profesional que necesita de la Estadística. Es, en el caso de tratarse de una comparación de medias, la diferencia mínima que interesa detectar, la diferencia mínima relevante desde el punto de vista médico, económico, lingüístico, etc. (Ver el Tema 9: Significación formal versus Significación material). Podríamos decir que esa d es el valor mínimo por el que tendría valor haber hecho la propia comparación. Un ejemplo, si se trabaja con pacientes hipertensos con media 160 y se ensaya un antihipertensivo se puede fijar una diferencia mínima a detectar de 20 (que baja a 140 la presión, como mínimo), puesto que si es menos de eso no será un buen antihipertensivo.

31. Existen fórmulas para casos específicos, como sucede con la siguiente fórmula para el Test de la t de Student de una muestra:

32. Observemos que esta fórmula es interesante para entender todos los conceptos de los que estamos hablando en este tema. Hay en el numerador del cociente interior al paréntesis dos constantes: una que depende de la alfa y otra que depende de la beta. Dependen, pues, ambas constantes, del error que estemos dispuestos a cometer en el proceso de decisión. Cuanto menor sea alfa y beta más grandes serán esas constantes y, por lo tanto, mayor será el tamaño de muestra. Además, como puede verse perfectamente en esta fórmula, en un contraste de hipótesis la determinación del tamaño de muestra es una función de cuatro variables.

33. Existen aplicaciones diferentes muy bien diseñadas para poder elegir el tamaño muestral necesario para un estudio determinado. Pero es fundamental entender todo lo comentado en este Tema para poder usar esas aplicaciones y saber interpretar lo que obtenemos con ellas. Y es básico, además, porque en esta aplicaciones lo primero que te piden es elegir qué tipo de estudio (si comparación de proporciones, de medias, de Odds ratio, etc) y después qué DE tienes, la diferencia mínima a detectar, la potencia que quieres tener, etc.

34. Un enlace excelente para practica todo esto es el siguiente:

http://www.imim.es/ofertadeserveis/software-public/granmo/

35. Unos comentarios para el uso de este enlace. Cuando se comparan dos poblaciones se pide la relación entre los tamaños de muestra. Si es que conviene o es inevitable tener más muestra en una u otra población. Si no es así se añade un 1, que simboliza que puede ser el mismo tamaño muestra. También pide una previsión de los valores que pueden perderse al ir analizando. Esto está pensando para casos donde sea previsible perder un porcentaje de muestra más o menos previsible. Si no se prevé pérdida se pone un 0 en esta opción. Por otro lado el manejo es bastante sencillo. La alfa suele elegirse 0.05, la beta 0.2 ó menos (por lo tanto, potencia 0.8 ó más), la DE la que podamos saber o prever y la diferencia a detectar la mínima que uno está dispuesto a aceptar como relevante antes de empezar el trabajo.

36. Y ahora un breve comentario final a las situaciones de muestras de poblaciones finitas. Nos referimos a situaciones donde la población es pequeña y puede modificar el tamaño de muestra. Hasta ahora estábamos bajo el supuesto de poblaciones lo suficientemente grandes como para considerarlas infinitas.

37. Veamos una fórmula usual que nos ayudará a aclarar las cosas:

38. Como puede verse es una modificación de una que hemos visto al iniciar este tema. La N es el tamaño de la población. Evidentemente si este valor es muy grande los dos cocientes donde participa se hacen tan pequeños que son insignificantes. Si, por el contrario, esta N es pequeña estos cocientes pueden modificar la n necesaria para tener un determinado tipo de precisión y deberemos tenerla en cuenta.

39. A continuación muestro una tabla donde se expresan los cálculos de estas n en condiciones diferentes (en función del radio r y del tamaño poblacional):

Los siguientes vídeos explican el tema:

 

1. La técnica de técnicas denominada Análisis de la varianza (ANOVA), del acrónimo Analysis of variance: ANalysis Of VAriance, tiene como objetivo básico la comparación de las medias de más de dos poblaciones.

2. El nombre de Análisis de la varianza, sin embargo, no es muy afortunado. En el ANOVA se comparan siempre las medias de varias poblaciones y se hace a través de un contraste de hipótesis donde se analiza la varianza, es cierto; pero no sólo eso, porque también se analizan las diferencias de medias que hay entre las muestras, y también, por supuesto, como siempre en Estadística, se analiza el tamaño de muestra.

3. Las técnicas de comparación siempre analizan estos tres elementos: dispersión, diferencias de medias y tamaño muestral. Por lo tanto, ANOVA es, en realidad, una metonimia: se habla del todo a partir de una parte. Porque, en realidad, la técnica que vamos a ver en este tema, se debería denominar: Análisis de la varianza, de la diferencia de medias y del tamaño muestral.

4. En el Tema 13: Introducción a las técnicas de comparación he explicado cómo influyen estos tres elementos (diferencia de medias, dispersión y tamaño de muestra) en las comparaciones de dos poblaciones. Lo visto allí es fácilmente generalizable a la comparación de más de dos poblaciones, porque el mecanismo de fondo usado para comparar más de dos poblaciones es, en realidad, equivalente al usado para comparar dos poblaciones.

5. Para entender bien la complejidad del ANOVA hemos de ver una serie de conceptos básicos que nos permitirán conocer el vocabulario que maneja el lenguaje de esta técnica. Tal vez sería interesante una primera lectura del artículo del apartado de COMPLEMENTOS Viaje en autobús turístico por el mundo ANOVA. En él se dibuja una introducción de cuáles son esos conceptos básicos del mundo ANOVA. En este tema vamos a ver los más importantes de estos conceptos.

6. El primero de esos conceptos es el de factor. Un factor en ANOVA es una variable cualitativa que genera o que contempla una serie de poblaciones a comparar. A estos grupos o poblaciones que un factor delimita se les denomina «niveles del factor». Pe: Imaginemos que estamos comparando el peso de un tipo de insecto en tres localidades distintas: diríamos que trabajamos con el factor localidad y que ese factor tiene tres niveles: las tres localidades concretas. Veamos unos datos posibles y cómo estarían estructurados:

7. Otro ejemplo: Supongamos que estamos comparando, en un estudio clínico, cuatro fármacos diferentes aplicados a una serie de pacientes diagnosticados de una determinada patología. Ahora tenemos el factor fármaco con cuatro niveles. La estructura que tendríamos ahora sería muy similar a la anterior pero con cuatro columnas en lugar de tres.

8. Otro concepto importante en ANOVA: Un factor puede ser fijo o aleatorio. Fijo es cuando los niveles que se estudian son los únicos niveles que interesan. Aleatorio es cuando los niveles que se estudian es una muestra de niveles. Lo que interesa, realmente, es decir cosas de una población de niveles, no de la muestra de niveles que hemos seleccionado para el estudio.

9. Supongamos el siguiente ejemplo: Estamos estudiando la calidad del producto fabricado por operarios en una empresa. Tenemos 50 operarios trabajando en la manufactura del producto que comercializa nuestra empresa.

10. Supongamos que queremos comparar al operario A, que es de nuestra confianza, es una referencia para nosotros, con los operarios B y C, que son operarios que queremos evaluar expresamente porque creemos que no elaboran el producto con la calidad deseada. Para ello se toma una muestra de cuatro productos fabricados por cada uno de estos tres operarios. Estamos en un caso de un factor fijo (el factor operario), con tres niveles. El ANOVA a utilizar sería, en este caso, un ANOVA de un factor a efectos fijos.

11. Supongamos que ahora lo que queremos es ver si entre los 50 operarios hay diferencias en cuanto a la calidad del producto elaborado y no podemos estudiar producto de los 50 operarios. Entonces seleccionamos tres operarios al azar y tomamos una muestra de cuatro productos fabricados por cada uno de esos tres operarios. Estamos ahora ante un caso de un factor aleatorio (el factor operario), de donde hemos tomado una muestra de tres operarios al azar. El ANOVA a utilizar sería, en este caso, un ANOVA de un factor a efectos aleatorios. Pero aunque detrás tengamos una finalidad diferente, la estructura de los datos será la misma, algo así como lo siguiente:

12. El ANOVA puede tener uno, dos, tres, cuatro, etc., factores. Sin embargo, lo más habitual es tratar con un número reducido de factores. Y cada uno de esos factores puede ser fijo o aleatorio.

13. Otro concepto importante en ANOVA: Cuando tenemos dos o más factores éstos pueden estar, entre sí, dos a dos, cruzados o anidados.

14. Dos factores están cruzados cuando todos los niveles de un factor se cruzan, se combinan, con todos los niveles del otro factor.

15. Supongamos que en un estudio clínico ensayamos dos tipos de antihipertensivos: un IECA y un ARA II. Cada uno es un factor y sus dos niveles son ausencia y presencia. Y se cruzan: o sea, unos pacientes son tratados con placebo (sin nada), otros sólo con IECA, otros sólo con ARA II y, finalmente, un grupo de pacientes es tratado con los dos antihipertensivos al mismo tiempo. Para simplificar supongamos que se trata a una única dosis, por eso los niveles por factor son únicamente dos: ausencia y presencia. Para ver cómo sería la estructura y la disposición de unos datos posibles observemos el siguiente ejemplo:

16. Son dos factores cruzados porque se combinan todos los niveles de un factor con todos los niveles del otro factor, como hemos visto. Observemos que la combinación No con No es el Placebo. Esta combinación unida a las otras tres posibles, según se combinen No con Sí, o Sí con Sí, configuran los cuatro cruces posibles entre dos factores cada uno con dos niveles.

17. Dos factores están anidados (uno dentro de otro) cuando los niveles de uno se combinan, jerárquicamente, entre los niveles del otro.

18. Supongamos, por ejemplo, que queremos ver la influencia que tienen, en los resultados de calidad de un producto, la máquina y el operario. Y tenemos cuatro tipos de máquinas y dos operarios. El primer operario trabaja en las máquinas 1 y 2, el segundo en la 3 y la 4.

19. Tenemos, pues, dos factores: máquina (con cuatro niveles) y operario (con dos niveles). Y están anidados. No están cruzados. Dos máquinas las usa un operario y las otras dos máquinas las usa el otro operario. Observemos cómo sería la estructura de unos datos posibles:

20. Obsérvese que el Operario A trabaja sólo con las Máquinas 1 y 2. Y el Operario B lo hace únicamente con las Máquinas 3 y 4. Esta es la disposición de los datos anidados o jerarquizados.

21. Si este mismo estudio lo hiciéramos con factores cruzados cada operario debería usar las cuatro máquinas y, entonces, los datos tendrían la siguiente estructura:

22. En ANOVA, como técnica de comparación que es, el objetivo es contrastar la Hipótesis nula de igualdad de niveles de un factor versus la Hipótesis alternativa de no igualdad de esos niveles. Esto se hace para cada factor contemplado en el ANOVA.

23. Además, en el ANOVA de dos o más factores cruzados, podemos valorar algo muy importante: la interacción entre factores.

24. Interacción entre factores significa que la variable estudiada, la variable dependiente, se comporta, ante niveles de un factor, dependiendo de cuáles sean los niveles del otro factor. O sea, que la variable estudiada tiene un valor que es función de la combinación que se dé de niveles. Después, con los ejemplos, se entenderá mejor esta importantísima noción.

25. En la sección HERBARIO DE TÉCNICAS de este Blog podremos ver cómo es cada una de las técnicas de ANOVA más importantes (hay que tener en cuenta que si se tienen dos factores, y no se dice lo contrario, esos factores están cruzados):

ANOVA de un factor a efectos fijos.

ANOVA de un factor a efectos aleatorios.

ANOVA de dos factores a efectos fijos.

ANOVA de dos factores a efectos aleatorios.

ANOVA de dos factores a efectos mixtos (uno fijo y uno aleatorio).

ANOVA de dos factores anidados a efectos fijos.

ANOVA de dos factores anidados a efectos aleatorios.

ANOVA de dos factores anidados a efectos mixtos.

ANOVA de un factor fijo con bloques aleatorizados.

ANOVA de cuadrados latinos.

26. En todas estas técnicas el objetivo básico será contrastar la hipótesis de igualdad o diferencia entre los distintos niveles en cada factor. Y si hay más de un factor y están cruzados contrastar la existencia de interacción entre esos factores. La importancia de diferenciar entre modelos diferentes es porque, como puede verse en cada uno de ellos, el cálculo de los p-valores para evaluar la significación es diferente según sean factores fijos o aleatorios, cruzado y anidados. Para ampliar todo esto ver el fichero Algoritmo de Bennet-Franklin.

27. Vamos a ver ahora algo muy importante en las técnicas ANOVA. Recordemos que la hipótesis alternativa en el análisis de cada uno de los factores es «la no igualdad de niveles».

28. Pero esta «no igualdad» puede ser por motivos muy diferentes. La igualdad de la H₀ es sólo una, pero la desigualdad de la H₁ puede tener paisajes muy diferentes. Supongamos, por ejemplo, un factor con cuatro niveles. La aceptación de H₁ puede ser porque los cuatro niveles son diferentes o porque dos son iguales, los otros dos también y las diferencias se dan entre esos dos grupos de niveles, etc.

29. Hay, por lo tanto, muchas formas de cumplirse la H₁. Si hay dos niveles sólo hay una posible H₁, que un nivel sea mayor que el otro; pero si hay más de dos niveles en un factor la H₁ contempla muchas alternativas posibles.

30. Pues bien, las técnicas llamadas «Comparaciones múltiples», también llamadas, en ciertos ámbitos, pruebas “Post hoc”, tratan de elegir una de esas muchas posibles afirmaciones que, de hecho, están comprimidas dentro de la Hipótesis alternativa, dentro de H₁.

31. Con estas técnicas dibujamos, perfilamos, concretamos, la forma de la H₁, lo que específicamente podemos afirmar en ella.

32. Existen diversas técnicas de Comparaciones múltiples: LSD de Fisher, Bonferroni, HSD de Tuckey, Duncan, Newman-Keuls, Scheffé (Ver Herbario de técnicas para ver en qué consisten cada una de ellas). Estas son las más usadas y las más prestigiosas. Todas hacen lo mismo pero con distinto nivel de conservadurismo. Unas ven antes que otras diferencias entre niveles. Sin embargo, cuando las cosas son claras todas esas técnicas trazan el mismo dibujo de la hipótesis alternativa. Sólo cuando hay dudas, cuando las diferencias no son muy claras, pueden aparecer diferencias. Para ver una visión comparativa de todas ellas ver el artículo Comparación entre técnicas de comparaciones múltiples.

33. Lo peculiar de estas técnicas es que, mediante un único contraste de hipótesis, se realizan múltiples comparaciones dos a dos. La idea nuclear de todas ellas es la creación de un umbral. Una diferencia de dos de las medias de los niveles del factor que esté por encima de ese umbral se considerará diferencia significativa y si, por el contrario, esa diferencia está por debajo de ese umbral se considerará una diferencia no significativa. Cada una de esas comparaciones múltiples crea un umbral distinto según un criterio diferente.

34. Es de esta forma cómo cada una de esas técnicas de comparaciones múltiples llega a establecer la posición relativa de un nivel respecto a todos los demás y se puede dibujar, así, con el nivel de información que tenemos, cuál es el mejor perfil concreto a asignar a la Hipótesis alternativa, a H₁.

35. El ANOVA necesita que se cumplan unas suposiciones. Básicamente tres: 1) Normalidad de los datos. 2) Igualdad de varianzas. 3) Independencia de los datos. En la sección Herbario de técnicas podrán verse las técnicas más usuales para comprobar estas suposiciones. El Test de la ji-cuadrado de ajuste a una distribución, el Test de Kolmogorov de ajuste a la distribución normal o el Test de Shapiro-Wilk, para la normalidad; el Test de Bartlett para la igualdad de varianzas o el Test de Durbin-Watson para la independencia.

36. De no cumplirse las condiciones hay que utilizar una técnica no paramétrica, como el Test de Kruskal-Wallis cuando tenemos un único factor.

37. Vamos a ver ejemplos de aplicaciones de la técnica ANOVA. Empezaremos con el caso de los primeros datos que hemos mostrado. Se trata de una estudio donde se compara el peso de un tipo de insecto en tres localidades distintas. El factor localidad y tiene tres niveles y se trata de tres localidades concretas, por lo tanto estamos ante un caso de ANOVA de un factor a efectos fijos. Recordemos los datos:

38. Antes de mostrar los resultados obtenidos podemos ver que la media de localidad 3 es la mayor. Es una media de 3.87. La media de la localidad 1 es 3.47. La de la localidad 2 está entre ellas: 3.67. El problema es: ¿Son estas diferencias estadísticamente significativas? El tamaño de muestra juega en contra de la significación. Hay sólo dos datos. Pero la dispersión es pequeña, esto iría a favor de la significación.

39. Si hacemos el análisis nos encontramos que el p-valor del contraste de hipótesis de igualdad de medias es 0.0331. Como es menor que 0.05 rechazamos la Hipótesis nula. Observemos la tabla ANOVA que es el procedimiento técnico para realizar este contraste de hipótesis:

40. Si comprobamos la normalidad de los datos, mediante el Test de Kolmogorov, tenemos un p-valor de 0.96, por lo tanto, como es mayor que 0.05 aceptamos la Hipótesis nula de normalidad (en los tests de bondad de ajuste a la normal la Hipótesis nula es normalidad). Si comprobamos la igualdad de varianzas, aplicando el Test de Bartlett, tenemos un p-valor de 0.66, lo que indica que podemos aceptar la Hipótesis nula de igualdad de varianzas. Con el Test de Durbin-Watson comprobamos que no haya autocorrelación entre los datos y tampoco la hay. Esto nos indica que se cumplen las principales suposiciones: la normalidad, la igualdad de varianzas y la independencia de los datos y que, por lo tanto, el p-valor que hemos calculado en la tabla ANOVA es fiable, está basado en unas suposiciones correctas.

41. Pero ahora debemos aplicar un Test de comparaciones múltiples para tratar de ver el porqué no hay igualdad entre las medias. Si aplicamos el Test LSD vemos que la localidad 1 no es distinta significativamente a la 2, la 2 no lo es tampoco de la 3 pero la 1 y la 3 sí que lo son. O sea, que el motivo del rechazo de la igualdad de medias es porque las localidades 1 y la 3 tienen insectos con peso significativamente distinto. Veamos a continuación un gráfico que ilustra extraordinariamente lo que estoy diciendo:

42. Se trata de un gráfico de los intervalos de confianza del 95% de la media de cada una de las localidades. Puede verse, perfectamente, que, en una mirada horizontal, la localidad 1 y la 2 tienen intervalos que se solapan. Pensemos que son intervalos de la media poblacional, por lo tanto, estamos hablando de que podría ser que la media poblacional de la localidad 2 estuviera por debajo de la media poblacional de la localidad 1, aunque la media muestral de la localidad 2 esté por encima de la media muestral de la localidad 1. Pensemos que estamos infiriendo, que la muestra es un medio, no un fin. Están (como diríamos en política con las horquillas) en empate técnico, cualquiera puede estar, poblacionalmente, por encima. Entre la localidad 2 y 3 sucede lo mismo: se solapan. Pero entre localidad 1 y 3 la separación entre intervalos de la media es clara. Por esto se rechaza la Hipótesis nula de igualdad de media en el ANOVA, por esta diferencia entre la localidad 1 y la localidad 3.

43. Y con esto habríamos concluido el análisis. Observemos todos los pasos. Observemos bien todo lo que hemos hecho y las conclusiones que al final sacamos.

44. Vamos a ver ahora otra aplicación. Supongamos el siguiente estudio:

45. Este es un caso interesante para visualizar un estudio donde es aplicable un ANOVA de dos factor a efectos fijos. Observemos que la media más baja es la de los tres valores de resistencia de la mucosa de los profesores que tomaron el placebo (No Vitamina A y No Vitamina E). Cuando toman sólo Vitamina A o sólo Vitamina E la resistencia aumenta en torno a una 20 unidades de mayor resistencia. Sin embargo, cuando se combinan ambas vitaminas la resistencia aumenta más que la suma de lo obtenido por una y otra vitaminas. No aumenta 40 sino que aumenta en torno a 60 unidades más. Esto es lo que nos detectará la interacción.

46. Se comprueban las suposiciones y todas se cumplen: normalidad, igualdad de varianzas e independencia. Aquí la tabla ANOVA nos proporcionará tres p-valores: uno para el factor vitamina A, otro para el factor vitamina E y otro para la interacción. Los tres son p-valores inferiores a 0.05, lo que indica que la presencia de cada una de las dos vitaminas aumenta la resistencia de la mucosa y que, además, al darse interacción significativa estamos ante la presencia de una correlación entre ambas vitaminas, que en este caso indica que la presencia de las dos conjuntamente producen una sinergia positiva.

47. Observemos a continuación el gráfico de interacción entre ambos factores:

48. Pueden observarse en este gráfico cuatro asteriscos: son las medias de las cuatro condiciones experimentales del estudio, que podríamos simplificar mediante las categorías: no-no, no-sí, sí-no, sí-sí. Observemos en el eje de las abscisas la no presencia y la presencia de Vitamina A y observemos, también, que los dos colores unen puntos con el mismo nivel de Vitamina E. El no-no es el placebo, es el valor más bajo. El sí-sí es el valor de media superior y observemos que su valor está muy por encima del que esperaríamos si no hubiera interacción. De no haber interacción esperaríamos que las dos rectas del gráfico fueran paralelas.

49. De la misma forma que en este caso vemos sinergia positiva podemos ver, en otros casos, sinergia negativa. Supongamos que en el gráfico anterior la recta roja en lugar de subir hubiera bajado cruzándose con la azul dibujando una X: estaríamos hablando también de interacción, pero la interpretación sería otra: diríamos que ambas vitaminas están en sinergia negativa; o sea, que cada una de ellas hace su efecto pero al combinarlas se pierde todo lo que individualmente hacen.

50. Vamos a ver un ejemplo de dos factores pero anidados:

51. Se trata de dos factores fijos, porque se han tomado cuatro hospitales concretos que quieren estudiarse, y dos fármacos también concretos. Son, además, dos factores que no están cruzados, están anidados. Observemos que el fármaco 1 se ensaya únicamente en los Hospitales 1 y 2 y que el fármaco 2 se ensayo sólo en los Hospitales 3 y 4. Estamos, pues, ante un ANOVA de dos factores anidados a efectos fijos.

52. Supongamos también que hemos ya comprobado la normalidad de los datos, la igualdad de las varianzas y la independencia de los datos. Ahora el ANOVA nos proporcionará dos p-valores sobre dos contrastes de hipótesis. Una hipótesis nula es la igualdad entre hospitales, la otra la igualdad entre fármacos.

53. Observemos los datos. ¿Qué podemos decir si los comparamos con detenimiento? Una cosa importante: se sabe Estadística cuando uno es capaz de saber lo que dará una técnica antes de aplicarla, mirando los datos. Mirémoslos, pues. ¿Qué se observa? Realmente si aprendemos a mirar estos datos aprenderemos las peculiaridades de un ANOVA de factores anidados.

54. Para ayudarnos a sacar conclusiones de nuestros datos, veamos los tres siguientes grupos de datos posibles:

55. Tenemos tres situaciones distintas. En el caso de arriba observemos que la diferencia está centrada entre fármacos. Al pasar del fármaco 1 al 2 es cuando vemos diferencias. Sin embargo, cuando estamos en un fármaco u otro entre hospitales no hay diferencias remarcables. Por lo tanto, hemos de pensar que en este caso habrá diferencia significativa entre fármacos pero no entre hospitales. Como así sucede si aplicamos la técnica ANOVA a estos primeros datos.

56. En el caso del medio observemos que la diferencia está centrada, ahora, entre hospitales. Al pasar del fármaco 1 al 2 no vemos diferencias, el patrón se repite. Sin embargo, cuando estamos en un fármaco u otro entre hospitales sí hay diferencias destacable. Por lo tanto, hemos de pensar que, ahora, en este caso, habrá diferencia significativa entre hospitales pero no entre fármacos. Como así sucede si aplicamos la técnica ANOVA a estos segundos datos.

57. En el caso de abajo observemos que la diferencia ahora es tanto entre fármacos como entre hospitales. Al pasar del fármaco 1 al 2 vemos diferencias, pero cuando estamos en un fármaco o en otro entre hospitales también se aprecian diferencias remarcables. Por lo tanto, hemos de pensar que en este caso habrá diferencias significativas entre fármacos y también entre hospitales. Como así sucede si aplicamos la técnica ANOVA a este tercer grupo de datos.

58. Si ahora volvemos a los datos reales del estudio planteado, observaremos que más bien estamos en un caso como el tercero de los datos ficticios. Parece que la variabilidad total que observamos tanto está canalizada hacia diferencias entre los dos fármacos como hacia diferencias entre los hospitales. Si aplicamos el ANOVA de dos factores anidados fijos a los datos del estudio vemos que tanto el factor Fármaco como el Factor Hospital presentan diferencias significativas, con un p-valor inferior a 0.05.

59. En todos estos ejemplos hemos visto alguna diferencia, sea de un factor, del otro, o de ambos, pero no nos olvidemos que podríamos encontrarnos también con datos como los siguientes:

60. Como puede apreciarse ahora, perfectamente, la variabilidad está centrada en la dispersión que hay dentro de cada uno de los cuatro grupos, no hay diferencias remarcables al cambiar de fármaco o al cambiar de hospital. Ahora todas las diferencias las vemos dentro de cada una de las cuatro situaciones experimentales. Lo que nos llevaría claramente a decir que ni el fármaco ni el hospital introducen ningún tipo de diferencias en la variable estudiada.

61. Hay una noción importante y útil en ANOVA que es necesario explicar: me refiero a la noción de bloque. Esto da lugar a una serie de modelos ANOVA que son muy utilizados.

62. En ocasiones un factor, que es el objeto básico de un estudio, a la hora de experimentar con él, de ensayar sus diferentes niveles, los ámbitos donde se aplica se sabe ciertamente, o se sospecha, que son ámbitos con importantes diferencias. Por ejemplo, supongamos que queremos ensayar tres tipos de abono y lo tenemos que hacer en cuatro terrenos que sabemos que son muy distintos desde el punto de vista químico y geológico. Esos cuatro terrenos actúan de bloques y lo que haremos es ensayar cada uno de los tres niveles del factor abono en cada uno de los cuatro terrenos, distribuyéndolos al azar dentro de ellos. El experimento quedaría así:

63. Este planteamiento da lugar a un modelo que se denomina ANOVA de un factor con bloques aleatorizados. Se trata de un modelo muy usado en diferentes ámbitos. Veamos un caso muy distinto del anterior: Supongamos que a unas personas es posible aplicarles todos los niveles del factor que se pretende estudiar, como podría ser, por ejemplo, que quisiéramos ensayar cuatro condiciones diferentes para ver cómo influye cada una de ellas en el valor de cierta variable (Por ejemplo, andar durante 5 minutos en ambientes con distinto grado de contaminación, el dolor después de la extracción de una pieza dental donde se han usado cuatro procedimientos distintos, valorar cuatro fórmulas distintas de un producto alimentario, etc). Y para ello tomamos a cinco personas a las que les aplicaremos esas cuatro condiciones en momentos diferentes y con un orden aleatorizado. Los resultados podrían ser los reflejados en la tabla siguiente:

64. Este caso, como el de los terrenos, es un caso de ANOVA de un factor con bloques aleatorizados. Ahora es la persona la que hace de bloque. Observemos que realmente cada individuo tiene un perfil característico y que en todos ellos se produce un mismo patrón: valor bajo en C1, sube en C2, sube más en C3 y baja hasta el mínimo en C4. Si no tuviéramos en cuenta a los bloques «personas» no habría diferencia significativa entre las medias de las condiciones por culpa de la enorme variabilidad que tenemos en el estudio. Sin embargo, el ANOVA de un factor con bloques aleatorizados compara las cuatro columnas de valores pero lo hace individuo por individuo. De esta forma capta la regularidad de estos cambios comentados y acabará diciendo que las diferencias muestrales entre las diferentes condiciones son diferencias estadísticamente significativas.

65. El ANOVA de un factor con bloques aleatorizados es un importante ejemplo de control de la dispersión con la finalidad de ver diferencias. Pensemos que la dispersión introduce un ruido que impide ver diferencias. Al introducir los bloques controlamos la dispersión, la explicamos. En el Tema 30: Ampliación de ANOVA veremos cómo a partir de este modelo podemos llegar a modelos un poco más sofisticados de control de la variación como es el ANCOVA o el ANOVA de medidas repetidas.

66. Ver estos ejemplos que hemos visto en este tema nos ayuda a situar lo que hacen las diferentes técnicas ANOVA que tenemos a nuestra disposición para comparar grupos diferentes. Son técnicas que comparan esos grupos en base a cómo está repartida la variación. Por eso se llaman Análisis de la varianza, porque realmente esto es lo llamativo, lo que más se ve, aunque, como ya hemos dicho, las diferencias de las medias entre los grupos y el propio tamaño de muestra los analiza también la técnica para decantarse por la igualdad o la diferencia entre las medias poblacionales de los grupos que compara.

67. En el ámbito del ANOVA se han introducido, también, aspectos de Significación material. Hemos dicho en el tema dedicado a la Significación formal y material que en Estadística el esfuerzo está principalmente dirigido a la Significación formal; o sea, a detectar diferencias entre poblaciones o relaciones entre variables, significativas, sin entrar en la valoración de aspectos de Significación material; o sea, de aspectos de Tamaño del efecto (en inglés “Effect size”), que suelen dejarse habitualmente en manos de los expertos en el campo concreto de aplicación: la medicina, la economía, la sociología, la biología, etc.

68. En la comparación de dos poblaciones suele usarse la d de Cohen para evaluar el tamaño del efecto. En el ANOVA se usa la eta cuadrada y la eta cuadrada parcial, cuyos cálculos son los siguientes:

 

69. Veamos la interpretación de estos dos cálculos: En la eta cuadrada se relativiza la suma de cuadrados; o sea, la variabilidad explicada por el factor o por el efecto estudiado, respecto a la suma de cuadrados total. En la eta cuadrada parcial se relativiza respecto a la suma de esa suma de cuadrados más la del error, la residual.

70. Como en todos los cálculos del Tamaño del efecto el tamaño muestral no tiene ninguna influencia, por eso únicamente juega en su cuantificación y valoración las diferencias de medias y las dispersiones y, en cambio, el tamaño de muestra no juega ningún papel.

71. Veamos unos ejemplos de ANOVA de un factor y de ANOVA de dos factores para ver cómo son esos cálculos e interpretar su papel:

72. Veamos, a continuación, dos casos de ANOVA de un factor:

73. Si hacemos una mirada a esos datos, antes de hacer el análisis estadístico, podemos ver que, en los dos estudios, las medias de los tres grupos, de los tres niveles del factor estudiado, son: 4, 5 y 6. Pero que en el caso de arriba los tres grupos están más separados, están más segregados. En el caso de abajo hay mucha dispersión intragrupo para el nivel de diferencia de medias que tenemos. Esto es lo que evalúa la eta cuadrada. Básicamente es eso.

74. Los resultados del ANOVA, en ambos casos, y del cálculo de la eta cuadrada y de la eta cuadrada parcial, seguiendo las fórmula mostradas anteriormente, son los siguientes:

75. Suele considerarse que una eta cuadrada en torno a 0,01 indica poco efecto, que una eta cuadrada en torno a 0,06 indica un efecto medio y que una eta cuadrada superior a 0,14 es ya un efecto grande. Observemos que en los datos de arriba tendríamos un tamaño del efecto grande y abajo un tamaño del efecto pequeño. Observemos que en el caso de un único factor la eta cuadrada y la eta cuadrada parcial coinciden en cantidad.

76. Los datos del caso de arriba muestran grupos más separados, muestran más efecto. Muestran, de hecho, un efecto grande. Sin embargo, no es estadísticamente significativo. Y en Ciencias primero es la Significación formal y luego la Significación material. Como en un juicio: primero hay que decir si el acusado es o no culpable, luego ya valoraremos si lo que ha robado es mucho o poco.

77. Observemos otro caso ahora con dos factores cruzados con interacción:

78. Si hacemos los análisis ANOVA de cada tabla y los cálculos de la eta cuadrada y de la eta cuadrada parcial tenemos el siguiente cuadro:

79. Podemos ver los cálculos de la eta cuadrada y la eta cuadrada parcial, que ahora, con dos factores, no coinciden, y podremos apreciar cosas como las siguientes: El factor 2 siempre presenta un tamaño del efecto grande y mayor que el producido por el factor 1 y por la interacción. Observemos en el cuadro de los valores de los estudios que realmente se produce un mayor salto de valores entre las dos filas que entre las dos columnas. Esto es lo que mide la eta cuadrado: donde se produce más salto y si éste es grande o es pequeño respecto a otras variabilidades que muestran los datos.

80. Estas medidas son muy interesantes, pero, siempre y cuando, previamente, se haya evaluado la Significación formal, que es, sin lugar a dudas, prioritaria. Por muchos millones que, presuntamente, haya robado una persona hasta que el tribuna no dicte culpabilidad, no formalice la culpabilidad, no podemos decir que materialmente se trata de un robo muy voluminoso. Si al final se comprueba la inocencia de aquella persona nos habremos equivocado mucho haciendo valoraciones materiales previas. Es importante, por lo tanto, situar bien estos cálculos que evalúan el tamaño del efecto.

81. El tamaño del efecto es, pues, en ANOVA, una forma de evaluar el peso relativo de la variabilidad, cómo está distribuido el reparto de cambios entre los distintos niveles de los factores estudiados. Y evalúa si estos cambios entre las medias de los diferentes grupos son grandes o pequeños relativizando estas diferencias respecto a la dispersión que hay en general y, más en concreto, dentro de los grupos (el error, o también llamado residuo).

Este tema está explicado en los vídeos siguientes:

1. Vamos a ver ahora técnicas estadísticas concretas de comparación de dos poblaciones.

2. Es muy importante ver con detalle cómo elegir, en una determinada situación concreta, la técnica adecuada entre las muchas disponibles.

3. Es muy importante elegir bien la técnica más adecuada en cada circunstancia para afinar así más la propia maquinaria de la técnica y que, de esta forma, las decisiones tomadas sean más fiables.

4. Voy a trazar un mapa de las técnicas más usuales de comparación de dos poblaciones y lo voy a hacer estructurado a modo de protocolo de actuación, de decisión.

5. Pensemos que dejamos una decisión trascendental (elegir entre H₀ y H₁) en manos de una maquinaria matemática, como es una técnica estadística, por lo que elegir la más ajustada al caso optimiza el funcionamiento de la propia técnica y su fiabilidad.

6. Protocolo de decisión entre técnicas de comparación de dos grupos:

Este mismo protocolo puede presentarse en forma de diagrama de flujo. Este gráfico lo ha elaborado un alumno de este curso (Bruno Splendiani):

Otras dos presentaciones de este mismo esquema me los ha facilitado Laura Ripoll muy amablemente:

Utilizad el que os resulte más cómodo.

 

7. Veamos con detalle el funcionamiento de este protocolo de actuación: Lo primero es ver si estamos ante una variable continua o dicotómica.

8. Se trata de ver si continuamos por el apartado 1 ó el 2 del protocolo. Si es una variable continua iremos por 1, si es dicotómica, por 2.

9. Supongamos que nuestro objeto de estudio es una variable dicotómica, con sólo dos valores posibles, por ejemplo: hombre/mujer, enfermo/sano, dolor/no dolor, opina A/opina B, etc. Estamos, claramente, en el punto 2. Y habremos de decidir si las dos muestras comparadas son independientes o relacionadas. En definitiva, si son dos poblaciones formadas por individuos distintos (independientes) o por los mismos individuos a los que se les mide la variable dicotómica en dos momentos distintos (muestras relacionadas).

10. Supongamos primero que estamos estudiando si la proporción de estudiantes mujeres en una facultad de Medicina y en una de Económicas es distinta. Tomaremos dos muestras, una de cada facultad, y veremos qué proporción de mujeres hay en cada muestra. Pe: obtenemos: 60% y 50%.

11. ¿Es esta diferencia estadísticamente significativa? Que hay diferencia muestral es evidente. 60% y 50% evidentemente son distintos. Pero esto es muestral, es diferencia muestral. Y nuestro interés es poblacional, como siempre. Debemos aplicar una técnica estadística para ver si esta diferencia es significativa, si es extrapolable a la población.

12. Deberemos aplicar un Test de comparación de dos proporciones, también llamado, sencillamente, Test de proporciones. Se trata de dos muestras claramente independientes. En éste, como siempre, en la H₀ tendremos la igualdad de proporciones poblacionales (p₁=p₂) y en la H₁ la desigualdad (p₁<>p₂).Y el p-valor del contraste de hipótesis nos dirá si, por el tamaño de muestra que tenemos, podemos considerar que esa diferencia del 10% es o no significativa. Esta misma situación resuelta por este Test de proporciones podría plantearse con el Test de la ji-cuadrado. De hecho, si repasamos los visto en el tema 8, una situación de comparación de proporciones puede resolverse, también, desde este Test de la ji-cuadrado.

13. El Test proporciones, para funcionar bien, requiere un tamaño muestral mínimo de 30 por grupo y que el producto del tamaño muestral por el tanto por uno esperado bajo la hipótesis nula del suceso que se analiza sea superior o igual a 5, en ambas muestras. Por ejemplo: Supongamos que tenemos una muestra de 50 por cada uno de los dos grupos a comparar. En una muestra tenemos sólo un caso del suceso analizado y en la otra tenemos 4 casos. Si la hipótesis nula (igualdad de proporciones) fuera cierta esperaríamos ver 5 casos de cada 100; o sea, un 0.05 por uno. Si multiplicamos este 0.05 por 50 nos da 2.5 sucesos esperados por grupo. Como es menor que 5 estamos fuera de las condiciones de aplicación de este Test de proporciones y deberíamos aplicar el Test exacto de Fisher.

14. Supongamos, ahora, que queremos ver antes y después de un determinado acontecimiento si un cierto número de personas opinan A o si opinan B (Por ejemplo, si votarían sí o no en un determinado referéndum). Habrá los que opinaban A y después B, los que opinaban A y continúan opinando A, los que opinaban B y luego continúan opinando B y, finalmente, los que opinaban B y pasan a opinar A. Es un claro ejemplo de muestras relacionadas. La variable es dicotómica pero es un mismo grupo de individuos a los que se les mide la misma variable en dos momentos distintos. Aplicaremos, en este caso, el Test de McNemar (Ver Herbario de técnicas).

15. Supongamos que ahora queremos ver el nivel de inglés de los estudiantes en esas mismas facultades vistas antes (Medicina y Económicas) mediante un examen con notas del 0 al 10, estaremos ahora ante una variable claramente continua.

16. Hay muchos valores posibles potencialmente entre 0 y 10. Estamos, ahora, en el apartado 1 de nuestro protocolo de decisión.

17. Y ahora no tenemos todavía el test a realizar, sino que debemos continuar examinando las especificaciones del protocolo y, nos tocaría, como siguiente paso, decidir si las muestras son independientes o relacionadas.

18. Aquí se trata de ver si los individuos de las dos muestras son los mismos o si son distintos.

19. En este caso que planteo, el del nivel de inglés de alumnos en dos facultades, es claro que se trata de dos muestras con individuos distintos. Se trata, por lo tanto, de muestras independientes.

20. Pero, imaginemos que en lugar de ser dos facultades, las estudiadas, fueran unos mismos estudiantes de una facultad (Pe: Medicina) y que tenemos el nivel de inglés de una muestra de estudiantes al empezar sus estudios universitarios y al final de esos mismos estudios. Y queremos comprobar si ha habido un cambio en ese nivel.

21. En este caso estaríamos ante muestras relacionadas. De unos mismos individuos tenemos dos medidas y queremos ver si hay diferencias. Es muy importante saber distinguir, pues, si las muestras son independientes o relacionadas (a veces se les denomina también apareadas, porque los valores van por pares: dos de cada individuo).

22. En el caso, pues, de las dos facultades, con muestras independientes, estaríamos en el caso 1a del protocolo y en el caso de una única facultad, con muestras relacionadas, estaríamos en el 1b.

23. El siguiente paso, que nos llevará a los apartados 1ai, 1aii, 1bi o 1bii del protocolo, es la comprobación de la normalidad, o no, de ambas muestras.

24. En el tema dedicado a Intervalos de confianza hemos hablado de la noción de ajuste de una muestra a una distribución normal. Y hemos presentado allí que la curtosis estandarizada y la asimetría estandarizada eran unos criterios útiles para comprobar el ajuste de una muestra a la distribución normal. Ahora hemos de dar un paso más y presentar la noción de comprobación estadística de la normalidad de una muestra mediante un contraste de hipótesis.

25. Para decidir si la variabilidad de una muestra sigue una determinada distribución, mediante un contraste de hipótesis, disponemos de las denominadas técnicas de «Bondad de ajuste».

26. Para la comprobación de la normalidad de una muestra existen diferentes técnicas de «Bondad de ajuste a la normal».

27. Todas ellas tienen la misma estructura:

H₀: Normalidad.

H₁: No normalidad.

Hay, pues, en Estadística, presunción de normalidad, porque la normalidad está en la Hipótesis nula.

28. Por lo tanto, en un Test de Bondad de ajuste a la normal con un p-valor superior a 0.05 mantendremos la suposición de normalidad. Estaremos ante una muestra que podríamos ver en el caso de tener en la población una distribución normal.

29. Como siempre en un contraste de hipótesis valoramos si lo que vemos en la muestra, lo que observamos en ella, encaja, es factible verlo, en el caso de ser cierto lo afirmado en la Hipótesis nula. O sea, que lo que vemos, lo Observado está dentro de la esfera de lo Esperado bajo la Hipótesis nula.

30. En cambio, si la p es inferior a 0.05 debemos rechazar la normalidad: la estructura de los datos no nos permiten pensar que la población de donde se ha tomado la muestra tenga una variabilidad en forma de campana de Gauss.

31. Los tests de bondad de ajuste a la normal más usados son el Test de la ji-cuadrado de ajuste a una distribución, Test de kolmogorov de bondad de ajuste a una distribución normal y el Test de Shapiro-Wilk (Ver Herbario de técnicas).

32. En las muestras independientes, para seguir por la vía 1ai las dos muestras deben seguir la normalidad. Si no es así seguimos por 1aii.

33. En las muestras relacionadas, apareadas, se suele calcular la muestra resta a partir de las dos muestras.

34. Como son una serie de individuos de los que se tienen dos valores: uno en cada muestra, se hacen las restas de los valores por individuo, creando una única muestra: la muestra de la resta de los valores de la variable en los dos tiempos o, en general, de los dos valores relacionados.

35. La normalidad se contrasta en esa muestra de restas obtenida a partir de los valores de las dos muestras relacionadas.

36. Si sigue la normal estaremos en 1bi y si no la sigue estaremos en 1bii. En el primer caso, siguiendo el protocolo, aplicaremos el Test de la t de Student para datos apareados (o relacionados) y, en el segundo caso, aplicaremos el Test de los signos o el Test de Wilcoxon (Ver Herbario de técnicas).

37. En muestras independientes, si no hay normalidad de las dos muestras (estamos, pues, en 1aii) aplicaremos el Test de Mann-Whitney (Ver Herbario de técnicas). A este Test también se le llama, a veces, Test de Mann-Whitney-Wilcoxon o, también, Test de Wilcoxon de la suma de rangos. Si, por el contrario, hay normalidad y, por lo tanto, estamos en el apartado 1ai, necesitamos realizar un nuevo paso.

38. Para decidir si aplicar el Test de la t de Student para muestras independientes y varianzas iguales o el Test de la t de Student para muestras independientes y varianzas distintas hay que aplicar un Test sobre las varianzas, un Test que nos permita decidir si las varianzas poblacionales son o no distintas.

39. El Test tiene la estructura de siempre: presunción de igualdad. De igualdad, en este caso, de varianzas o de desviaciones estándar.

40. El contraste es: H₀: σ₁=σ₂, H₁: σ₁<>σ₂. El Test más conocido y usado para resolver este contraste es el denominado Test de Fisher de igualdad de varianzas o también llamado Test de Fisher-Snedecor (Ver Herbario de técnicas). Evidentemente estamos hablando de Desviaciones estándar poblacionales, no muestrales. El problema es, ahora, decidir si las diferencias muestrales entre las Desviaciones muestrales nos permite pensar que son inferibles a nivel poblacional, o no.

41. Si el p-valor es mayor que 0,05 mantendremos la hipótesis de iguadad y aplicaremos, entonces, para comparar las medias de las dos poblaciones, el Test de la t de Student de varianzas iguales.

42. Si el p-valor es menor que 0,05 rechazaremos H₀, aceptaremos H₁ y aplicaremos el Test de la t de Student de varianzas desiguales.

43. Con esto tenemos, pues, explicado todo el mapa trazado en el esquema del protocolo.

44. Las diferentes técnicas de la t de Student son técnicas llamadas «paramétricas», porque para funcionar bien necesitan que las variables sigan una distribución concreta: la distribución normal.

45. El Test de Mann-Whitney, el Test de los signos y el Test de Wilcoxon son, por el contrario, técnicas llamadas «no paramétricas». Estas técnicas precisan pocas condiciones previas.

46. Observemos que se trata de técnicas donde las variables no necesitan seguir una distribución concreta: ni una dicotómica ni una normal.

47. Estas técnicas sólo precisan la continuidad de las variables; o sea, que sean variables con muchos valores posibles.

48. Las técnicas de la Estadística no paramétrica son técnicas «todo terreno». Aplicables en muchas más situaciones. Al no precisar una determinada distribución son más versátiles.

49. Esta mayor versatilidad la pagan con menor potencia: Son técnicas más conservadoras que las denominadas paramétricas, lo que significa que cuesta más rechazar la hipótesis nula. Tienen menor capacidad de detectar diferencias.

50. Una peculiaridad de las técnicas no paramétricas es que los contrastes de hipótesis no son sobre la media sino que lo son sobre la mediana; o sea: H₀: Mediana₁=Mediana₂ y H₁: Mediana₁<>Mediana₂, o sobre la igualdad o desigualdad entre las distribuciones.

 

1. En la Regresión lineal múltiple modelizamos la relación entre una variable dependiente y dos o más variables independientes mediante una función lineal, una función que será, ahora, no una recta, como sucedía con la Regresión lineal simple, sino un plano (si tenemos dos variables independientes) o un hiperplano (si tenemos más de dos variables independientes).

2. En la Regresión lineal múltiple el punto de partida es el mismo que en la Regresión lineal simple. Se pretende modelizar la relación entre unas variables con la finalidad última de poder pronosticar una de ellas: la variable dependiente, a partir del conocimientos de las otras: las variables independientes. En la Regresión lineal múltiple se introducen nuevas variables independientes con la finalidad de reducir la dispersión de la predicción, con la finalidad de disminuir el residuo.

3. El modelo matemático es, ahora:

y=a₁x₁+a₂x₂+…+a_dx_d+b+e

donde a_1, a_2,…, a_d y b son los coeficientes del modelo y donde e es el residuo, que, como en la Regresión lineal simple, supondremos que sigue una distribución normal N(0, DE).

4. Aunque la Regresión lineal múltiple es, en buena parte, una generalización de la Regresión lineal simple, tiene unas particularidades que conviene precisar.

5. Una de sus peculiaridades es la tendencia a llenar excesivamente el modelo. Hay la tendencia a ir introduciendo variables, hinchando el modelo y esto es muy perjudicial. Para que las cosas funcionen lo mejor posible conviene trabajar con variables que sean independientes entre ellas.

6. Observemos que en el punto anterior he usado la noción de independencia entre variables para referirme a las variables que se denominan independientes en el modelo de regresión. Recordemos que de esas variables tendremos, en el futuro, valores concretos para un individuo y a partir de ellos trataremos de pronosticar el valor de una variable dependiente que desconoceremos su valor para ese individuo.

7. Pueden observarse dos nociones de independencia distintas, pues, en lo que estamos diciendo ahora. Una cosa es la posición de las variables en el modelo de Regresión y otra es el que las variables sean independientes entre ellas, que significa que la correlación entre ellas sea cero.

8. Cuando no se cumple esta relación de independencia entre las variables independientes se produce un fenómeno de colinealidad. Esto es perjudicial para el modelo. El perjuicio representa que las estimaciones de los parámetros del modelo (los coeficientes), que son los elementos básicos para la construcción de los pronósticos de la variable dependiente, tienen más Error estándar. Y el Error estándar, como Desviación estándar de una predicción, es uno de los principales criterios de calidad de una estimación.

9. Hay distintos mecanismos para comprobar si tenemos un exceso de colinealidad. El Test de Belsey, Kuh y Welsch (Ver Herbario de técnicas) es uno de los más usados para comprobar si tenemos ese exceso de colinealidad. Ante un exceso de colinealidad conviene hacer una revisión y una nueva consideración de las variables independientes a usar en el modelo de Regresión, eliminando alguna de ellas o haciendo una Análisis de componentes principales (Técnica multivariante que veremos más adelante).

10. De hecho, parece lógico, en una Regresión lineal múltiple, pedirle a las variables independientes que sean independientes entre ellas. Pensemos que si no lo son, si tienen un cierto grado de dependencia, es porque de alguna forma comparten aspectos entre ellas, en cierta forma dicen cosas similares esas variables. Por lo tanto, a la hora de ser usadas para predecir una variable dependiente se produce un fenómeno de redundancia: estamos usando varias veces lo mismo para pronosticar algo. Y esto se paga con más imprecisión en las estimaciones.

11. Otra peculiaridad de la Regresión lineal múltiple es la posibilidad de construir el modelo paso a paso. Es el procedimiento denominado, en inglés, Stepwise.

12. Al realizar una Regresión lineal múltiple hay, pues, tres modalidades de estimación del modelo:

a. Forzando la entrada en el modelo de todas las variables elegidas.

b. Mediante un Stepwise hacia delante. La Regresión entonces se denomina Fordward Stepwise Regression.

c. Mediante un Stepwise hacia atrás. La Regresión entonces se denomina Backward Stepwise Regression.

13. Expliquemos las dos variantes últimas, puesto que la primera no precisa ninguna explicación.

14. El Stepwise hacia delante lo que hace es, paso a paso, ir introduciendo, en el modelo de Regresión lineal, como dice su nombre: paso a paso, variables independientes, hasta completar el mejor modelo posible.

15. En primer lugar crea un modelo con una única variable independiente. En realidad, pues, el primer paso es crear una Regresión lineal simple. Pero lo hace eligiendo entre todas las variables independientes la que consigue un mejor modelo, si es que lo consigue. En este primer paso debe existir entre las variables independientes una variable que tenga una relación significativa con la variable dependiente. De lo contrario el procedimiento acabaría aquí y no tendríamos modelo matemático para relacionar esas variables.

16. En el segundo paso se prueba de introducir, entre las variables independientes que quedan, cuál es la que consigue un modelo mejor, si es que alguna lo consigue. Se trata de establecer unos criterios de calidad mínimos. Lo que se denomina un Criterio de entrada. Si no se alcanzan nos quedamos con una Regresión lineal simple y se rechazan las otras variables.

17. Si hemos conseguido introducir en el modelo una segunda variable independiente se valora, probando con todas las variables independientes que quedan, la posibilidad de introducir una tercera. De nuevo se aplican unos criterios de entrada que si no se alcanzan no se introduce ninguna variable más.

18. Y así se va haciendo hasta alcanzar el mejor modelo. Es importante tener en cuenta que en cualquiera de estos pasos hay la posibilidad de extraer una variable que anteriormente se había introducido. Y cambiar así la disposición inicial. Por ejemplo, supongamos que en los pasos anteriores se habían introducido las variables x₃ y x₅ y, al probar una nueva introducción, al ensayar con, por ejemplo, x_7, el procedimiento observa que consigue mejores resultados sacando del modelo la variable x₃ que había sido la primera que había introducido, quedando, entonces, el modelo con x₅ y x_7.

19. El Stepwise hacia atrás es lo mismo pero ahora partiendo que hemos empezado forzando la entrada de todas las variables dentro del modelo y, a continuación, en el siguiente paso, mirar de sacar una de las variables independientes: una variable que al sacarla alteremos la calidad del modelo menos que un valor umbral establecido, lo que se denomina, ahora, un Criterio de salida. Si es así, si podemos extraer sin perjudicar por encima de ese valor preestablecido, reducimos el modelo.

20. Y así, paso a paso, pero en sentido contrario, vamos creando el mejor modelo posible, la mejor ecuación posible que relacione una variable dependiente con varias variables independientes.

21. Los criterios de entrada y de salida, que en muchas ocasiones son el mismo valor, generalmente vienen dados por el valor de un estadístico, por el valor de la F de Fisher. Puede verse en el Herbario de técnicas, en concreto, la técnica “Contraste de hipótesis de la pendiente de Regresión” que valores de F pequeños implican buena relación entre la variable dependiente y la independiente. Y valores grandes implican mala relación. Pues el criterio de entrada será que el valor de la F esté por debajo de cierto valor y el de salida que esté por encima de también de cierto valor, que suele ser el mismo. En otras ocasiones el criterio de entrada o de salida es un determinado p-valor prefijado asociado al parámetro de la variable que se decide si entra o no en el modelo.

22. Dados unos datos muestrales de una serie de individuos donde tengamos de ellos los valores tanto de la variable dependiente como de todas las variables independientes, cualquiera de los tres procedimientos estima los coeficientes del modelo y el valor de la Desviación estándar del residuo; o sea, de ese elemento que sumamos a cualquier procedimiento de Regresión.

23. Todos estos coeficientes debe decidirse si son coeficientes significativos, valores fiables que nos proporcionan una modelo asentado, estable, que refleja una realidad no sólo muestral, sino una realidad poblacional.

24. Para que todas estas estimaciones y estas significaciones proporcionadas, mediante p-valores, por técnicas estadística, sean fiables es necesario que se cumplan algunas condiciones que ahora comentaré.

25. No olvidemos que toda la llamada Estadística paramétrica se construye con procedimientos cuyas decisiones y cuyas construcciones se basan en unas suposiciones, bastante exigentes, que deben cumplirse.

26. Por otro lado las suposiciones que ahora comentaré son condiciones compartidas con la Regresión lineal simple. Habitualmente la mayor parte de software estadísticos que realizan Regresión lineal, tanto la simple como la múltiple, y, en ésta última, tanto los dos tipos de Stepwise como la que fuerza la entrada de todas las variables independientes, sus inferencias se basan en estas suposiciones.

27. Una de las comprobaciones necesarias a hacer en estos modelos es que realmente los residuos sigan la distribución normal N(0, DE). Suposición nuclear en la Estadística paramétrica. Y fundamental para el buen funcionamiento de la mayor parte módulos de Regresión lineal en los distintos software comerciales.

28. Una de las técnicas para comprobar esta normalidad es el Test de la ji-cuadrado de bondad de ajuste a una distribución. Otra muy utilizada es el Test de Kolmogorov.

29. Otra comprobación importante es la Homogeneidad de varianzas. Esto significa que el residuo tienen una dispersión homogénea, igual, sean cuales sean los valores de las variables independientes. Hay diversas pruebas que se han desarrollado para comprobar si se cumple o no esta condición. Una es el Test de Glesjer.

30. Otra comprobación importante es que no haya autocorrelación entre los valores en su orden de obtención. Que sean valores independientes uno respecto a otro. El Test de Durbin-Watson es el apropiado en estos casos. La independencia de los datos entre sí es una suposición también del modelo de Regresión lineal.

31. Otra consideración importante a investigación en una Regresión es la influencia de cada punto. No todo punto tiene la misma influencia. Es importante que no haya puntos excesivamente influyentes. Que las estimaciones de los parámetros del modelo queden demasiado en manos de esos puntos. Entre muchos criterios existentes uno de los más usados es el criterio de Cook (Ver Herbario de técnicas) para la detección de influencia.

32. Cuando alguna o varias de las condiciones necesarias no se cumplen una de las opciones más usuales es la Regresión no paramétrica. En este ámbito los métodos más usados se basan en la utilización de estimaciones de funciones de densidad no paramétricas.

33. De hecho, los diferentes procedimientos de Regresión no paramétrica, tanto simple como múltiple, se basan en procedimientos de construcción, sobre el terreno, partiendo de la muestra, donde habrá una enorme flexibilidad que vendrá dada porque la función irá siempre a remolque de la posición de los valores muestrales que tengamos.

34. Posiblemente el modelo de Regresión no paramétrica más utilizado es el Estimador de Nadaraya-Watson que se puede consultar en la sección Herbario de técnicas.

35. Finalmente un criterio de calidad de una Regresión lineal múltiple, como sucede también en la Regresión lineal simple, es el Coeficiente de determinación, la R² (Ver Herbario de técnicas). Aunque el valor de este coeficiente es un número que va del 0 al 1 es frecuente expresarlo en tanto por ciento. Es una forma de expresar el grado de determinación de la variable dependiente por parte de las independientes.

Los siguientes vídeos explican el tema:

 

1. En la introducción de las técnicas de relación mostraba el importante gráfico siguiente:

2.. Recordémoslo: En la primera fila del dibujo se ven tres situaciones bien distintas de relación entre dos variables cuantitativas.

3. En la segunda fila del dibujo se ven tres situaciones distintas de relación entre dos variables cualitativas, ejemplificada en un caso de relación entre dos variables dicotómicas.

4. Y, finalmente, en la tercera fila del dibujo se ven tres situaciones distintas de relación entre una variable cuantitativa  y una variable dicotómica.

5. Si se observa el dibujo completo con detenimiento se captará el paralelismo que hay en las tres situaciones planteadas, en las tres filas.

6. En cada una de las filas hay una relación inversa en el primer caso, una no relación en el segundo y una relación directa en el tercero

7. Para medir la relación entre variables continuas tenemos la correlación de Pearson, la de Spearman y la de Kendall, que ya hemos comentado en el tema dedicado a la correlación.

8. El caso de la izquierda tiene una correlación negativa, el de la derecha positiva y en el caso del centro no hay correlación (r=0).

9. Para medir la relación entre variables dicotómicas ya sabemos que tenemos distintos índices. El más importante de ellos, el más usado, es la Odds ratio.

10. Ahora, en la segunda fila, al relacionar dos variables dicotómicas, el caso de la izquierda y en el de la derecha tendremos una Odds ratio distinta de uno, uno mayor que uno y otro menor que uno, según coloquemos los valores en la tabla, y en el caso del centro una Odds ratio de uno.

11. Para medir la relación entre una variable continua y una dicotómica, que es la situación dibujada en la tercera fila del gráfico, también se usa una Odds ratio. Veremos luego de qué forma se adapta esta noción a un caso tan distinto como éste.

12. En esta situación tercera, que es la que ahora nos va a ocupar, el caso de la izquierda del dibujo tendrá una Odds ratio menor que uno, el de la derecha mayor que uno y el del centro tendrá una Odds ratio muy próxima a uno.

13. Para situar a la Regresión logística veamos primero el caso de la relación entre una variable dicotómica con una única variable independiente continua. Se suele denominar una Regresión logística simple. Luego veremos que esto se puede ampliar a más de una variable independiente y hablaremos, entonces, de Regresión logística múltiple.

14. Veamos cómo es la función matemática que relaciona una variable dependiente dicotómica «y», con valores de 0 y 1, con una variable independiente «x» continua. El valor de 1 lo reservamos siempre al acontecimiento que especialmente queramos detectar, los casos, en términos médicos (Ver el Tema 9). El valor 0 lo asignamos a los que van asociados al acontecimiento contrario: los controles, en términos médicos.

15. En los tres gráficos de la tercera fila, que es el caso que ahora planteamos, veremos que no tiene sentido allí usar una recta para representar esos datos. Debemos usar una función no lineal un tanto especial. Pero veamos primero, intuitivamente, esta situación en unos casos posibles. Supongamos los siguientes casos con datos factibles. Veamos, en primer lugar, que hay una mayor cantidad de valores con la variable dependiente con el valor 0. Y veamos que los valores de arriba; o sea, los valores con el valor 1, se van desplazando, en los diferentes gráficos, hacia la derecha:

A la hora de construir una función que modelice las proporciones de valores abajo (valor 0) y arriba (valor 1) debemos establecer unas curvas como las siguientes:

16. El tipo de función que se adapta mejor a valores que se estructuran en dos líneas paralelas es el llamado modelo de Regresión logística simple.  Veamos la fórmula general de ese modelo de Regresión y las formas de las curvas que puede dibujar este modelo:

17. Esta función tiene dos parámetros: la «a» y la «b». Veamos qué papel juega cada uno de ellos a la hora de configurar la mejor adaptación de una función de ellas a unos datos concretos que tengamos en una muestra determinada:

18. El parámetro «b» es el elemento más importante del modelo de regresión logística. Obsérvese que puede ser positivo, cero o negativo.

19. Es cero cuando no hay relación entre la variable dicotómica y la variable continua. Y su valor absoluto marca el grado de relación.

20. De hecho, la Odds ratio, como medida de la relación entre estas dos variables, es:

21. Si b=0, la OR vale 1 (e⁰=1), que significa que no hay relación.

22. Cuando la «b» es positiva la OR será mayor que 1 y cuanto mayor sea evidentemente mayor será la OR.

23. Cuando la «b» sea negativa, la OR será menor que 1 y cuanto mayor sea, en valor absoluto, menor será, entonces, la Odds ratio, será un valor más próximo a cero.

24. Recordemos que la Odds ratio puede tomar valores de cero a infinito. Mayor o menor que uno indica que hay relación. Cuanto más alejada de 1 más relación. El que sea menor o mayor que 1 indica un diferente tipo de asociación entre la variable cuantitativa y la variable dicotómica.

25. Es cierto que la Odds ratio tiene un rango de valores un poco especial. De cero a infinito, con el uno como punto de bifurcación. Punto que separa dos tipos cualitativamente distintos de relación.

26. A un lado y al otro del 1 tenemos dos espacios infinitos de valores. Del 1 a infinito es tan infinito como del 0 a 1.

27. Es cierto que es un tanto peculiar la asimetría que hay en cuanto al aspecto de los dos espacios a derecha e izquierda del 1 en la OR.

28. Estamos acostumbrados a la correlación donde el espacio que hay desde el -1 al 0 es el mismo que el que hay del 0 al 1.

29. Pero a la hora de posibilidades de expresar una relación son exactamente las mismas las que hay con la correlación de las que hay con la OR.

31. Una OR=100 es equivalente a una OR=0.01, una OR=10000 a una OR=0.0001, y así. Equivalen pero marcan relaciones de distinto tipo, claro.

32. Para entender bien cuándo tenemos relaciones fuertes o débiles es muy importante mirarse y remirarse bien los ejemplos mostrados en el gráfico anterior.

33. El valor absoluto de la b será grande, y por lo tanto la OR estará muy alejada de 1, si los puntos con valores 0 ó 1 están muy segregados, si la transición del 0 al 1 ó del 1 al 0 es muy rápida.

34. Obsérvese, en el gráfico anterior, que al estar los puntos segregados tiene más lógica crear una función con mucha pendiente.

35. Y una pendiente más grande significa una b con mayor valor absoluto y, por lo tanto, un valor de e^b, una OR, más alejado de 1.

36. Cuando los valores con 0 ó 1 están poco segregados entonces la pendiente de la función es baja, el valor absoluto de la b es pequeño y la OR es, entonces, un valor próximo a 1. Lo que indica que hay poca relación entre la variable continua y la dicotómica.

38. En una regresión logística debe, evidentemente, evaluarse su significación estadística. Una forma de hacerlo es mediante la significación estadística de la OR.

39. Y la significación de una OR, ya lo hemos visto, se puede valorar mediante un p-valor o mediante un intervalo de confianza del 95%.

40. Por ejemplo, una información así: OR=2, IC 95%: (0.2, 20), es equivalente a una información así: OR=2, p>0.05. No es significativa.

41. Y una información así: OR=1.33, IC 95%: (1.23, 1.44), es equivalente a una información así: OR=1.33, p<0.05. Ahora sí es significativa.

42. En una OR para que un IC del 95% nos indique significación el intervalo no debe contener el 1. Es lógico que sea así. Si el intervalo contiene al 1, indica que hay confianza de que el verdadero valor poblacional pueda ser 1.

43. Una peculiaridad de la OR vista aquí, respecto a la vista en el Tema 9, es que depende de las unidades de la variable independiente. Una OR=2 significa que por cada unidad de aumento de la variable independiente x, doblamos el riesgo de que suceda lo que la variable dicotómica delimita. Si queremos cambiar de unidades debemos hacer un cambio de escala. Veamos a continuación un ejemplo para la variable independiente Edad. Si la variable es en años y obtenemos un valor de b de 0,1 y, por lo tanto, una OR de 1,105 eso significa que cada año de aumento de edad aumenta en 1,105 el riesgo. Si queremos ver qué pasa en intervalos de 10 los debemos aplicar el siguiente cálculo que nos lleva a una OR de 2,718. No cometamos el error de multiplicar la OR por 10:

44. En la regresión logística múltiple el problema es el mismo pero ahora las variables predictoras, las variables independientes, son más de una.

45. La ecuación de la regresión logística múltiple es la siguiente: ‪

46. Es una ecuación equivalente a la vista en el modelo anterior de Regresión logística simple. El recorrido de la función sigue siendo 0 y 1, pero el dominio es, eso sí, ahora, multidimensinal.

47. Supongamos que tenemos sólo dos variables independientes: x₁ y x₂. El espacio dibujado por ellas es, entonces, un plano.

48. Si ahora añadimos la variable dependiente dicotómica «y» a las dos variables independientes x₁ y x₂ se dibuja un espacio tridimensional.

49. En este caso al representar los puntos muestrales éstos ocupan dos planos, uno a altura y=0 y el otro a altura y=1.

50. La ecuación de la regresión logística múltiple con dos variables independientes es la siguiente:

51. En la regresión logística múltiple hay un procedimiento de elección de las variables independientes que influyen en la dependiente.

52. Y ese procedimiento consiste en una generalización a más variables de lo que hemos visto en la regresión logística simple.

53. Las variables independientes que se relacionan con la dependiente tendrán sus coeficientes, las a₁, a₂, con alto valor absoluto.

54. Las variables independientes que no se relacionan con la dependiente tendrán sus coeficientes con valores muy próximos a cero.

55. Si consideramos la regresión logística múltiple de dos variables independientes la posición de los puntos en los dos planos es clave a la hora de ver qué variables independientes influyen en la dependiente y cuáles no, cuáles tienen valores absolutos grandes y cuáles no, cuándo únicamente influye una variable, cuándo influyen las dos y cuándo no influye ninguna.

58. En el gráfico siguiente se ven cuatro casos con posiciones de puntos bien distintas con sus respectivos coeficientes:

59. Comentemos los cuatro casos del gráfico anterior y así veremos cómo la distribución de los puntos en los dos planos es clave.

60. En el caso que ocupa la posición de arriba a la izquierda los valores están distribuidos igual por los dos planos. Aquí no hay relación posible. Por eso tanto a₁ como a₂ son iguales a cero, no son diferentes significativamente a cero. Ni x₁ ni x₂ se relacionan con la variable y.

62. En el caso de arriba a la derecha los valores están en posiciones diferentes en los dos planos. Y la diferencia es atribuible a la x₁. Es, pues, aquí la variable x₁ la que está en relación con la variable y. Por esto el valor absoluto de a1 es grande y a₂=0.

64. En el caso de abajo a la izquierda los valores están también en posiciones diferentes en los dos planos. Y ahora es debido a x₂. Es, pues, aquí la variable x₂ la que está en relación con la variable y. Por esto el valor absoluto de a₂ es ahora grande y a₁=0.

66. En el caso de abajo a la derecha los valores están también en posiciones diferentes en los dos planos. Y debido tanto a x₁ como a x₂. Ahora las dos variables están en relación con la variable y. Por esto tanto el valor absoluto de a₁ como el de a₂ son grandes.

68. Cuando la relación de una variable independiente con la variable dependiente es fuerte el valor absoluto del coeficiente es grande.

69. Como decía antes, y es muy importante, cuando los valores con y=0 e y=1 están más segregados es posible crear más pendiente en la función.

70. En cambio si la segregación es sólo parcial debe establecerse un suave pase de un nivel al otro, lo que implica pendiente pequeña.

71. Para calcular la Odds ratio debe elevarse, como en la Regresión logística simple, el número e al valor del coeficiente correspondiente.

72. La OR de la variable x₁ es, pues, e^a₁ y la de la variable x₂ es e^a₂.

El siguiente vídeo explica el tema:

1. En las técnicas de relación el objetivo básico es detectar relación entre variables. La focalización está puesta, en este tipo de técnicas, en las variables, no en las poblaciones que pueda haber en el estudio. Los protagonistas son las variables y detectar covariación entre ellas, detectar que la variación que vemos en una de ellas tiene conexión con la de la otra.

 2. El primer paso, como veremos en temas sucesivos, será, en primer lugar, valorar si existe o no esta relación (si es estadísticamente significativa), si esta relación la podemos cualificar entre diferentes tipos de relación (relación directa, inversa, etc) y, finalmente, si la podemos cuantificar a través de un procedimiento estandarizado que nos permita saber entre qué valores se puede mover esta relación desde un mínimo a un máximo.

 3. Veremos que cuando hayamos hecho este primer orden de cosas pasaremos a tratar de modelizar matemáticamente esta relación mediante la Regresión. Con ella, además de modelizar esa relación, de crear un dibujo de su morfología, podremos hacer previsiones de unas variables a partir del conocimiento de valores de otras variables, y esto tiene una importante trascendencia en Ciencia.

 4. Para introducir las técnicas de relación que iremos viendo en temas sucesivos es importante ahora ya destacar que es fundamental diferenciar si la relación es entre variables cuantitativas, entre variables cualitativas o entre variables cualitativas y cuantitativas.

 5. Iremos viendo con detalle las peculiaridades de estas diferentes situaciones. A modo de introducción planteo el gráfico siguiente:

 

6. Se trata de un gráfico muy importante que irá saliendo en diversos temas donde se hable de aspectos concretos de las técnicas de relación.

7. Observemos en él que hay tres filas de datos. En la primera se visualizan tres situaciones de relación entre variables cuantitativas. En la segunda fila se ven tres situaciones de relación entre variables cualitativas. En la tercera fila, finalmente, se ven tres situaciones donde se relaciona una variables cualitativa con una de cuantitativa.

8. Estos tres casos ejemplifican e introducen conceptos esenciales en todo lo que vamos a ver en las técnicas de relación.

9. Observemos que el caso central, en las tres filas, es un caso en el que no parece haber relación entre las variables. Se trata de dos variables sin relación, sin covariación conjunta, donde cualquier valor de una variable puede estar combinado con cualquier valor de la otra variable. Esto, precisamente, es lo característico de una situación donde dos variables no tienen relación. En Estadística hablamos, en casos así, de dos variables independientes.

10. En las tres filas, por el contrario, a la izquierda y a la derecha nos encontramos con casos donde sí parece haber relación. Saber el valor de una variable de ellas nos parece informar del valor que pueda llegar a tener la otra variable. Esto es indicativo de relación y de lo que en Estadística llamamos variables dependientes.

11. Observemos, también, que a izquierda y a derecha, podemos decir que la relación es como opuesta, es cualitativamente distinta, como invertida. Esto también nos podrá interesar detectarlo porque nos indicará tipos diferentes de relación entre variables.

12. A esta relación que se aprecia en los ejemplos de la izquierda y de la derecha, en las tres situaciones posibles, también le podríamos valorar una cantidad que midiera el grado de esta conexión entre variables.

13. Pues con todo ello hemos visto, de momento muy intuitivamente, lo esencial de las técnicas de relación: detectar si existe o no esta relación, si esta relación la podemos cualificar en tipos de relación y, finalmente, si la podemos cuantificar de alguna forma.