Una noción misteriosa en Estadística es la noción de potencia. Pero es una noción muy importante que conviene delimitar con mucha precisión.

En un proceso de decisión entre dos estados posibles, como ocurre en Estadística en el contraste de hipótesis, siempre podemos cometer dos errores diferentes y, también, como contrapartida, dos aciertos diferentes. Veamos el siguiente gráfico:

Una cosa es nuestra elección y otra cosa distinta es lo que es cierto. Como es una tabla de dos por dos, hay cuatro situaciones posibles. Dos de acierto y dos de error.

El error de tipo I es el denominado nivel de significación. Este error lo fijamos nosotros y normalmente se elige el valor de 0.05. Recordemos que el contraste consiste en elegir una zona de la distribución del estadístico de test usado para el contraste que tenga esa baja probabilidad bajo la H₀ y que esté en una zona donde pese mucho la H₁. El criterio de decisión es, entonces, el siguiente: Si el valor del estadístico de test cae en esa zona nos inclinaremos por rechazar la Hipótesis nula, de lo contrario no la rechazaremos, la mantendremos.

El error de tipo II, por el contrario, no está prefijado. La distribución del estadístico de test tiene una dispersión muy distinta dependiendo de la dispersión de la variable estudiada y del tamaño de muestra; o sea, dependiendo del Error estándar. Pero esa distribución será distinta según sea cierta la Hipótesis nula o lo sea la Hipótesis alternativa. Y, además, esas distribuciones al aumentar el tamaño de muestra con la que nos basamos para tomar decisiones, van segregándose, van separándose más. Esto hace cambiar el error de tipo II porque al optar por mantener la Hipótesis nula la probabilidad de que la Hipótesis alternativa sea cierta se reduce muchísimo. En definitiva, el error de tipo II viene dado por las condiciones concretas del test. Al tratar con muestras pequeñas el Error estándar es alto y las distribuciones bajo la Hipótesis nula y bajo la Hipótesis alternativa se solapan mucho. Sin embargo, al tratar con muestras grandes el Error estándar se reduce mucho y esas misma distribuciones se separan y es más factible tomar decisiones con menos posibilidades de error de tipo II.

La potencia es el complementario de ese error de tipo II. Potencia más Error de tipo II suman 1 ó, en tanto por ciento, suman 100. Por lo tanto, minimizar el error de tipo II supone, automáticamente, maximizar la Potencia.

Vamos a ver, todo esto, gráficamente. Observemos el siguiente gráfico:

La distribución de la izquierda es la distribución supuesta si es cierta la hipótesis nula. Supongamos que es un test unilateral y contrastamos, en la alternativa, que la media es mayor que un cierto valor prefijado en la nula. Por lo tanto, la zona de rechazo de la hipótesis nula está hacia la derecha. Se construirá, entonces, una zona crítica de rechazo, de probabilidad 0.05 (la alfa), que es la zona roja. Si el valor del estadístico es donde apunta la flecha y construyo una distribución con media en ese punto y con la misma dispersión que en la nula podemos calcular todos los valores que nos interesan. La beta, la 1-beta (la potencia). Y esto se expresaría así:

donde P(A/B) significa la probabilidad de decir A si es cierto B.

En este caso dibujado la beta es muy grande (próxima a 0.5) y la potencia, por lo tanto, es pequeña. En un contraste de hipótesis es muy importante tener potencia elevada. Una potencia igual o superior a 80% se considera ya una potencia elevada. De esta forma minimizamos la posibilidad de equivocarnos en nuestras decisiones. El 5% del error de tipo I es fijo y el error de tipo II lo debemos hacer lo más pequeño posible. Esto lo conseguimos con contrastes basados en muestras lo suficientemente grandes para alcanzar estos valores de referencia. Así conseguimos crear en Estadística procedimientos de decisión de mayor calidad, procedimientos más fiables, con menos errores.

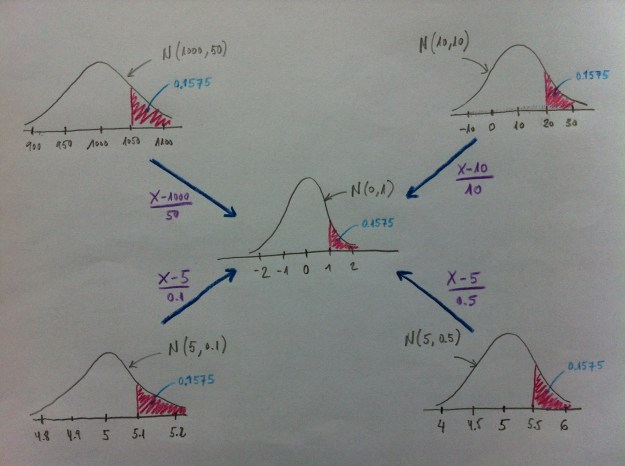
La dispersión de estas curvas dibujadas depende del error estándar que tengamos; o sea, de la DE y de la n. La DE no depende de nosotros, pero la n sí. Veamos cómo quedan dibujados los diferentes conceptos implicados:

Podemos aumentar el tamaño de muestra del estudio. Si aumentamos el tamaño de muestra nos encontraremos con una situación considerablemente mejor. Menor beta y mayor potencia:

Tenemos, ahora, un contraste muy bueno. Con una beta muy baja y una potencia elevada.

Suele decirse que una baja potencia nos sirve para delimitar aquellas situaciones en las que no rechazamos la Hipótesis nula muy posiblemente por tener tamaños de muestra pequeños. Esto es cierto. Muchas veces, tamaños de muestra pequeños impiden ver diferencias que existen en la realidad. Pero la potencia, también, nos puede servir para criticar un estudio en el que ha salido un p-valor inferior a 0.05. Si es un estudio con poca potencia tampoco tiene el nivel de fiabilidad que, a priori, le podríamos dar viendo el p-valor que vemos.

De hecho, para darle una vuelta más a este importantísimo concepto estadístico, se puede decir que con la potencia tenemos un segundo mecanismo de seguridad en un contraste de hipótesis. Es como asegurarse más de las decisiones. Si sólo tuviéramos el nivel de significación, el p-valor, tendríamos menos protección. Al añadir la potencia tenemos un segundo mecanismo de seguridad, de control.

Por lo tanto, en un contraste no basta tener un p-valor pequeño sino tener una potencia grande. Observemos los tres gráficos mostrados a continuación. En los tres veremos que el valor del estadístico cae en zona crítica; o sea, el p-valor es menor que 0.05 pero la potencia es completamente distinta. El tamaño de muestra en el primer caso es bajo y por eso hay mucha dispersión en la distribución del estadístico de test. Sin embargo, el caso del medio y, especialmente el de abajo, en el que hay más tamaños de muestra progresivamente, conseguimos, al tener menor error estándar, separar más la distribución bajo la hipótesis nula y bajo la hipótesis alternativa (que es la construida sobre el valor obtenido en el estadístico de test). Ambas distribuciones se van separando cuanto más tamaño de muestra tengamos. Esto genera una situación de mayor potencia.

Supongamos los dos casos que se plantean a continuación:

A la izquierda estamos comparando dos muestras de tamaño 3 con una diferencia de medias considerable (las medias muestrales son 10 y 25) y  con una Desviación estándar de 10. El p-valor que obtenemos es de 0.29, luego mantendríamos la Hipótesis nula de igualdad de medias. Pero mediante un calculador de la potencia, como el GRANMO, tenemos que la potencia es del 46%; o sea, que el error de tipo II es del 54%. Esto es demasiado error. El estudio no sería aceptable.

A la derecha estamos comparando dos muestras de tamaño 10 con una diferencia de medias considerable (las medias muestrales son, también, aquí, 10 y 25) y  con una Desviación estándar de 15. El p-valor que obtenemos es de 0.048, luego rechazaríamos la Hipótesis nula de igualdad de medias. Pero mediante un calculador de la potencia, como el GRANMO, tenemos que la potencia es del 61%; o sea, que el error de tipo II es del 39%. Esto es, también, demasiado error. El estudio no sería aceptable.

Por lo tanto, con la potencia tenemos un segundo mecanismo de control, un segundo nivel de seguridad. El p-valor nos ayuda a decidir si hemos de mantener la hipótesis nula o pasarnos a lo que dice la hipótesis alternativa, pero la potencia da un segundo nivel de control. Una potencia elevada (superior al 80%) nos dirá que la interpretación que hagamos del p-valor está basada en un contraste lo suficientemente fiable desde el punto de vista del tamaño de muestra.

Por lo tanto, es muy importante, antes de hacer un estudio, delimitar el tamaño de muestra necesario para tener la potencia mínima exigible. De esta forma optimizamos el proceso de decisión.

Todo esto que acabamos de ver puede quedar complementado con el Tema 16: Determinación del tamaño de muestra que es un ámbito en el que la noción de potencia adquiere una importancia capital.

Veamos los tres casos siguientes:

Son tres ejemplos donde si hacemos una t de Student de varianzas iguales tenemos un p-valor inferior a 0.05 (marcado en rojo) pero mediante el calculador de tamaño de muestras GRANMO se observa que la potencia es muy baja. Menor del mínimo aceptable del 80%.

Cuando se realiza, en Estadística, un contraste de hipótesis, se formulan dos hipótesis: La Hipótesis nula y la Hipótesis alternativa. En esas hipótesis hay afirmaciones. La intersección entre ellas debe ser vacía; o sea, no pueden tocarse, no pueden decir lo mismo, puesto que debemos decidirnos por una u otra.

La Hipótesis nula parte con ventaja porque, a priori, se toma como cierta. En ésta solemos escribir las afirmaciones de lo que podemos decir antes de hacer nada. Y en la Hipótesis alternativa suele estar escrito lo que debemos demostrar, lo que únicamente se puede decir si hay detrás una buena masa de datos que lo certifica.

Entonces se toma una muestra o varias muestras, según lo que estemos haciendo, y se le calcula o se les calcula lo que se denomina un estadístico de test. Este estadístico tiene una determinada distribución ante una población o unas poblaciones determinadas y ante un tamaño muestral o unos tamaños muestrales determinados. Pero observemos que al final siempre se acaba con la misma expresión:

que significa que la distribución de este estadístico T es F(x) en el caso de ser cierta la Hipótesis nula. Las tres rayitas horizontales significan “distribuido”. Solemos decir “bajo la Hipótesis nula” en lugar de “en el caso de ser cierta la Hipótesis nula”, que significa lo mismo y solemos escribir el H₀ debajo de las tres rayitas horizontales.

Las distribuciones F(x) de esos estadísticos de test T pueden ser muchas, dependiendo del caso, pero las más usuales son la Distribución t de Student, F de Fisher, N(0,1), ji-cuadrado.

Y entonces se crean en esa distribución dos zonas bien distintas: la zona donde sería más posible tener valores si fuese cierta la Hipótesis nula y la zona donde sería más posible tener valores si fuese cierta la Hipótesis alternativa y tenemos entonces con distribuciones distintas gráficos como los siguientes:

Observemos que se dibujan esas dos zonas donde es más verosímil una Hipótesis o la otra. En todos los casos se crea una zona amplia, grande, de probabilidad normalmente de 0.95 para la Hipótesis nula y una zona pequeña, restringida, de probabilidad generalmente de 0.05 para la Hipótesis alternativa.

De esta forma se construye un Test cualquiera, un contraste de hipótesis de los cientos o miles diseñados históricamente en Estadística. La estructura es siempre la misma.

Una vez diseñado se hacen las observaciones muestrales y se ve dónde cae lo que vemos. En función del criterio preestablecido decidimos finalmente, a la luz de lo que vemos, si mantenemos la Hipótesis nula o si, por el contrario, la rechazamos y nos pasamos a afirmar lo que dice la Hipótesis alternativa.

Gauss, que era un matemático genial, tuvo una extraordinaria intuición: en la naturaleza muchas cosas se distribuyen de forma simétrica respecto a un valor central y cuanto más se alejan de ese centro menos densidad de valores hay. Y creó una función de las más importantes de la historia de las matemáticas: la Distribución normal, o también conocida como campana de Gauss. (Si se quiere ver la situación de la Distribución normal dentro del contexto de otras funciones de distribución consultar el artículo Funciones de distribución).

La Distribución normal tiene una propiedad muy importante: Si a una variable con una Distribución normal cualquiera se le resta su media y se la divide por su desviación estándar se transforma en una Distribución normal con media 0 y con Desviación estándar igual a 1. Es la llamada Distribución normal estándar. Y a este procedimiento, a esta transformación de una normal cualquiera en una única y común distribución, la N(0, 1), se le denomina “estandarización” o “tipificación”.

Al restar por su media la normal se desplaza, rígidamente, sin cambiar su forma, sin cambiar su dispersión, hasta situarse sobre el cero. Al dividir por la Desviación estándar (DE) lo que hacemos es comprimirla (si la DE de partida es mayor que 1) o expandirla (si la DE de partida es menor que 1). En el gráfico adjunto se pueden ver estos dos actos: el de desplazamiento y el de compresión.

Esta propiedad de la Distribución normal nos permite calcular el área de cualquier de una de ellas mediante una única tabla, la de la Normal N(0, 1).

¿Y cómo funciona la tabla de N(0, 1)?

Hay de muchos tipos de estas tablas. Todas deben usarse sabiendo dos cosas básicas: Que el área que hay debajo de la campana es 1 y que la distribución de áreas es simétrica respecto al valor donde está el punto medio.

Voy a explicar cómo se utiliza una de estas tablas. La tabla adjunta tiene unos valores referencia en la primera columna y en la primera fila. En la primera columna los valores son 0.0, 0.1, 0.2, y así sucesivamente. En la primera fila son 0.00, 0.01, 0.02, y así sucesivamente. Las áreas en esta tabla se dan siempre hacia la izquierda del número de referencia elegido. Cuando en una N(0, 1) se quiere buscar un número para encontrar el área debe elegirse la combinación de un número de la primera columna con un número de la primera fila, sumándolos.

Practiquemos: Si quiero calcular el área que hay, bajo la campana, a la izquierda de 1.43, debo buscar en la primera columna el 1.4 y en la primera fila el 0.03. De esta forma sumo estos dos valores tengo 1.43. En la celdilla intersección de tal columna con tal fila encontramos el valor de tal área: 0.9236. Esta es el área a la izquierda de 1.43, el área desde menos infinito hasta 1.43 bajo la distribución N(0, 1).

Si quiero calcular, ahora, el área a la izquierda de 0.82 debo buscar en la primera columna el 0.8 y en la primera fila el 0.02, así al sumar tengo 0.82. En la celdilla intersección de tal columna con tal fila encontramos el valor de tal área: 0.7939.

Observemos que los valores empiezan en el punto 0.0. Esto es con finalidad de ahorrar espacio. Porque al ser el área bajo la campana de 1 y a partir de la propiedad de simetría podemos calcular cualquier área. Veámoslo: Supongamos que queremos calcular el área a la izquierda del valor -1.13, debemos buscar el área a la derecha de 1.13 porque es la misma. Y para encontrarla hay que buscar el área a la izquierda de 1.13 y calcular 1 menos esa área. Jugando con esta idea se puede calcular cualquier área.

Si se quiere encontrar el área dentro de un intervalo, por ejemplo entre 0.23 y 1.12, buscamos el área a la izquierda de 1.12, el área a la izquierda de 0.23 y las restamos. Las restamos porque al área a la izquierda de 1.12 hay que restarle el área a la izquierda de 0.23, de esta forma estaremos calculando el área que hay desde 0.23 a 1.12.

Y, así, sabiendo utilizar las propiedades de la Distribución normal comentadas: área 1 y simetría, puede calcularse cualquier área.

Hay un detalle que es importante destacar. Ahora que ya sabemos manejar la tabla de la Normal hemos de decir que cuando decimos aquello de media más menos una Desviación estándar (DE), más menos dos DE o más menos tres DE, cubren el 68.5, 95 y 99.5% podemos comprobar que estos valores son aproximados, no son exactos. Se fijan estos tres números porque son muy próximos y son más fáciles de retener en la memoria. En realidad, si lo calculamos exacto desde -1 hasta +1 en la N(0, 1) sería exactamente: 0.8413-0.1587=0.6826; por lo tanto media más menos una DE es exactamente un 68.26%. Si miramos la tabla podremos comprobar que desde -2 hasta 2 hay un área un poco superior al 95%, y que si queremos crear un intervalo exactamente del 95% deberíamos crearlo mediante la media más menos 1.96 Desviaciones estándar porque desde -1.96 hasta 1.96 se da exactamente un área de 0.95. Respecto al intervalo formado por la media más menos tres DE el área es: 0.99865-0.00135=0.99730; o sea, del 99.7%.

Para ver problemas de aplicación de la distribución normal y ver su relación con otras distribuciones puede consultarse el artículo Funciones de distribución. Allí se verá, entre otras cosas, cómo la distribución normal se puede usar para aproximar a distribuciones como la Binomial o la Poisson.