Vamos a ver, en siete breves temas, una introducción a las matemáticas necesarias para seguir un curso de Estadística. Este curso está pensado, especialmente, para estudiantes de Psicología, pero puede ser útil para aquellos estudiantes van a estudiar una asignatura de Estadística en cualquier grado universitario.

1.Los conceptos de entidades y variables.

Entidad, en ciencia, es cualquier unidad que interese estudiar aisladamente. Este es el punto de partida de cualquier ciencia: delimitar las entidades a estudiar. Ejemplos de entidades: pacientes, empresas, consumidores, plantas, microorganismos, etc.

En matemáticas y estadística esas entidades están siempre presentes pero como en un segundo plano. Lo fundamental, lo que estudiamos en ciencias son las variables asociadas a esas entidades.

Las variables son características de las entidades. Son valores numéricos o no numéricos que se les asigna a cada entidad. Ejemplos: edad, altura, tiene o no diabetes, número de empleados, etc.

Dos tipos de variables:

a) Cuantitativas: cuando los valores son numéricos.

b) Cualitativas (también denominadas categóricas o nominales): cuando los valores son no numéricos. Cuando esas variables cualitativas tienen sólo dos valores posibles se les denomina dicotómicas.

2.El concepto de matriz de datos:

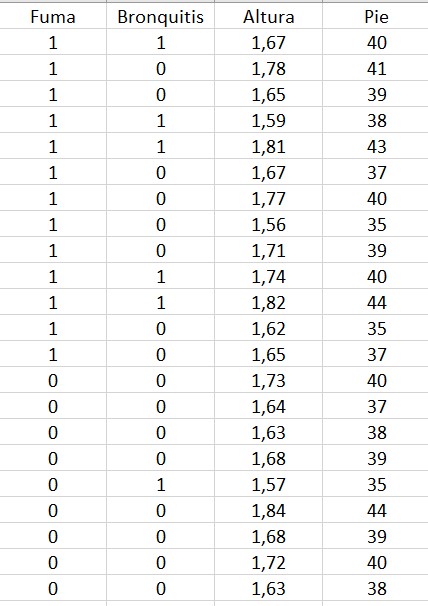
En las matrices de datos se acostumbra a codificar el SÍ como 1 y el NO como 0.

3.Números, orden, intervalos.

Se manejan muchos números en Estadística, números que hay que saber interpretar y manejar.

Un número muy importante en Estadística es, por ejemplo, la correlación.

La correlación es un número que está entre el -1 y el +1.

Mide, primero, si hay o no relación entre dos variables cuantitativas.

Si hay relación evalúa, entonces, el tipo de relación que tienen (positiva o negativa) y la cantidad de relación (valor absoluto de la correlación).

Si no hay relación; o sea, si la correlación es 0, entonces no se evalúa nada más.

El siguiente esquema puede servir de patrón de interpretación:

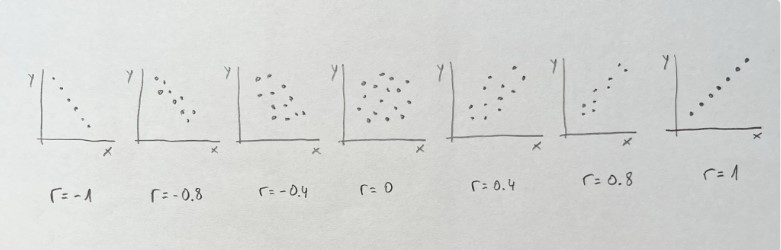
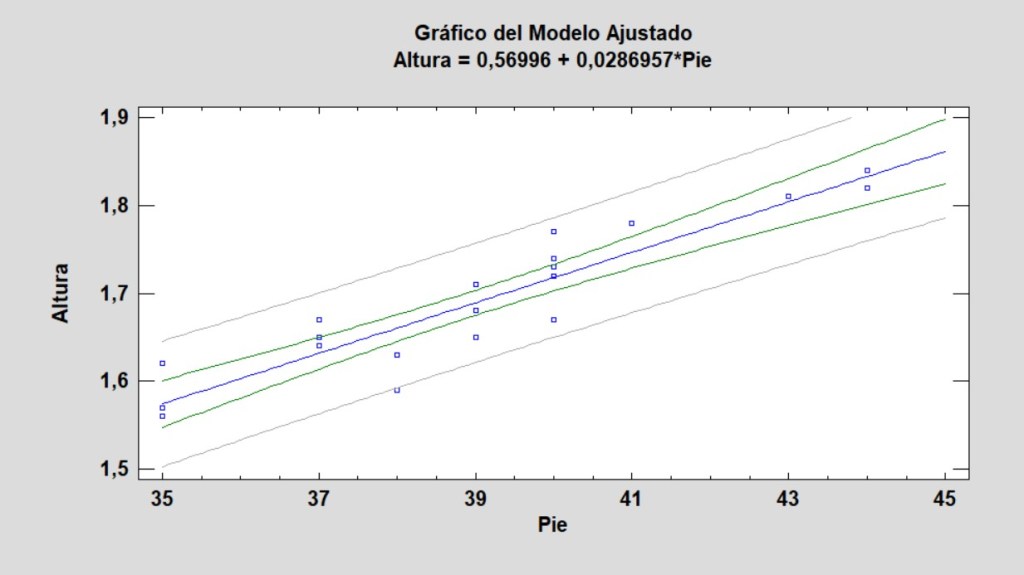
Miremos el cálculo de la correlación entre la variable Pie y la variable Altura en nuestra base de datos:

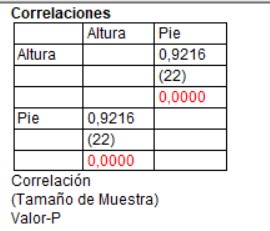
Miremos el gráfico de nuestros datos:

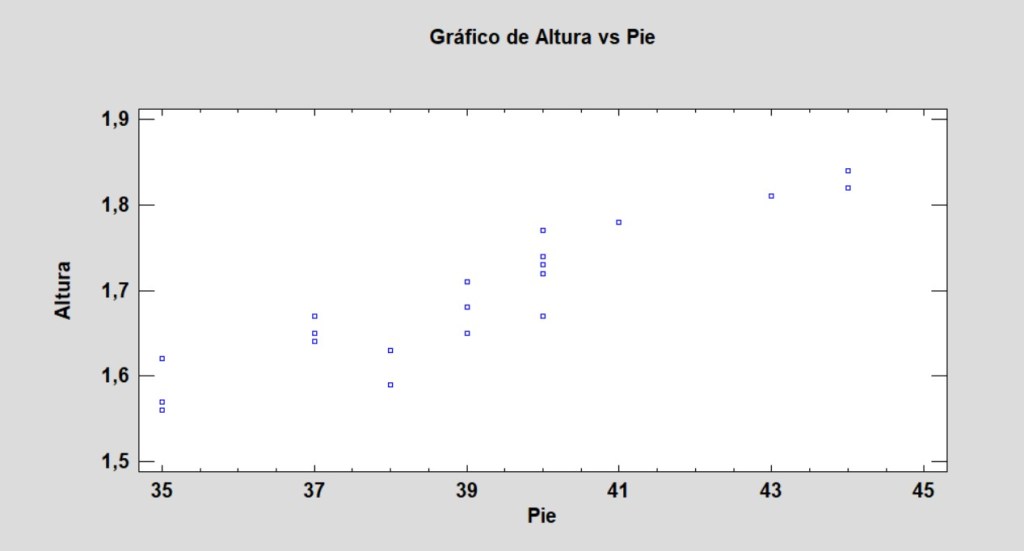
Otro número muy importante en Estadística es la Odds ratio. Mide la relación que hay entre dos variables cualitativas dicotómicas.

Observemos, previamente, este gráfico:

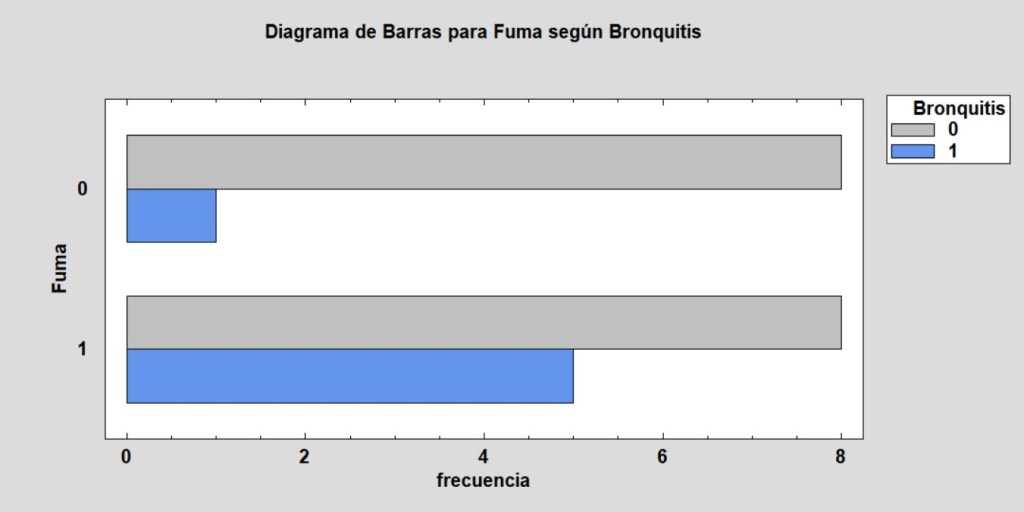
Puede apreciarse perfectamente que fumar está asociado con la bronquitis.

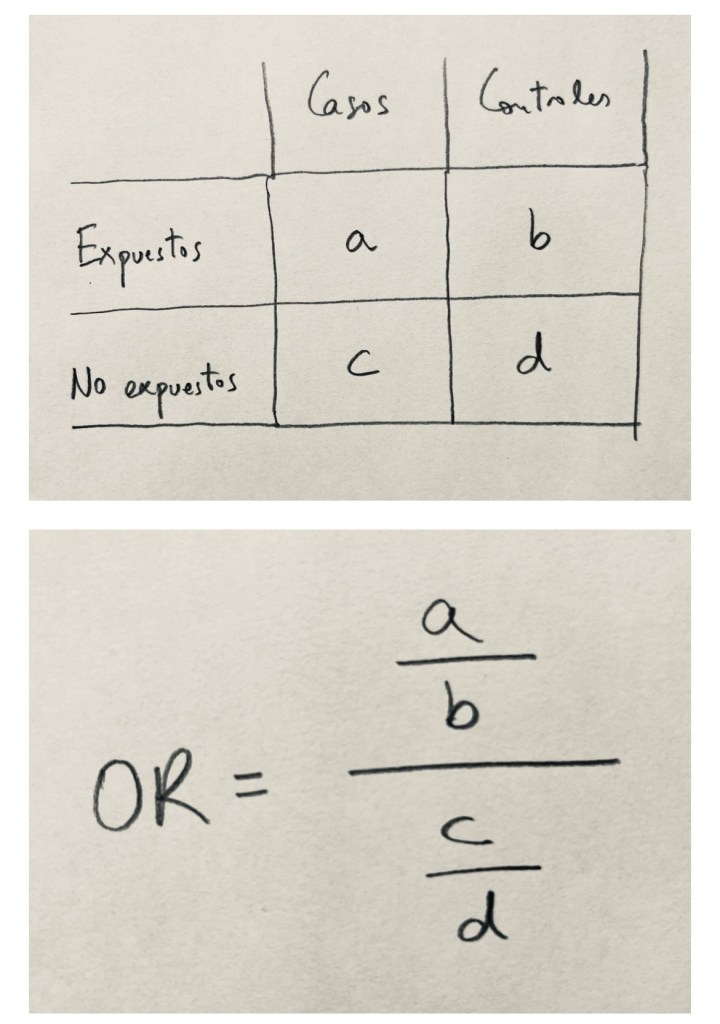
En la siguiente calculadora de Odds ratio se puede apreciar el cálculo de la Odds ratio:

Podéis ir cambiando los valores y veréis cómo cambia la Odds ratio.

Observad en el Excel cuál es la fórmula del cálculo:

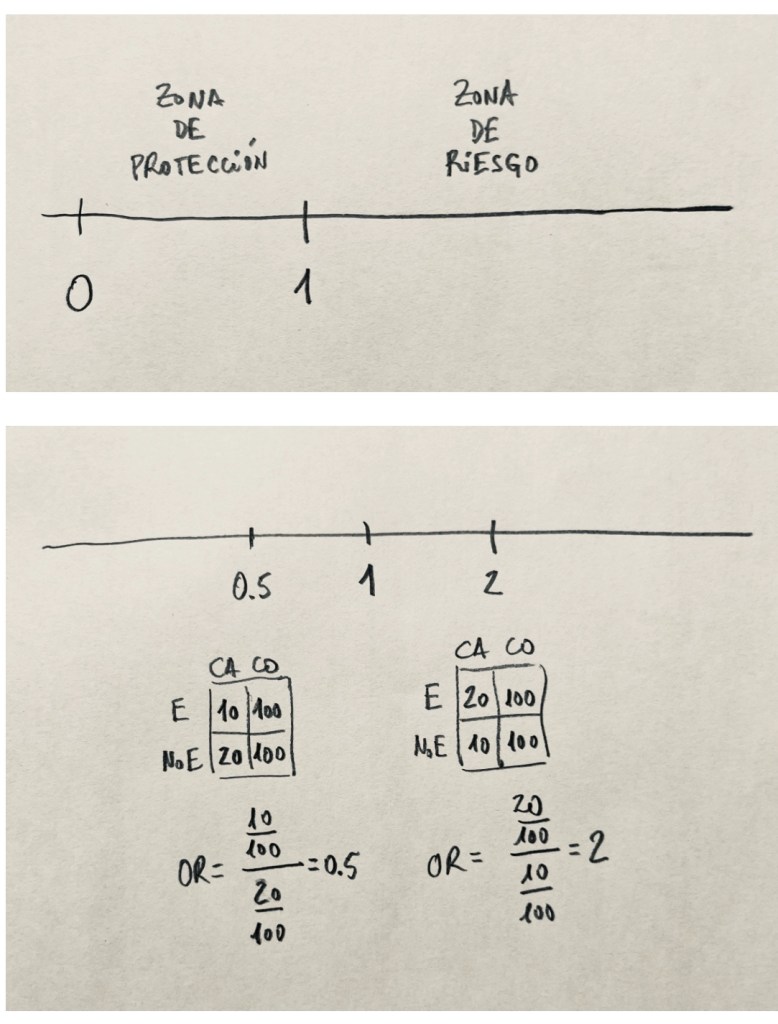
Observemos en el gráfico anterior que hay una equivalencia entre una OR de 0.5 y una de 2. Porque en un caso y otro se han intercambiado la Exposición y la No exposición.

También es interesante ver, en la calculadora del Excel, el Intervalo de confianza del 95% (IC 95%). Como prática es interesante ver si el 1 está dentro o no del intervalo. Esto, como lo veréis a lo largo del curso de Estadística que hagáis, es crucial. Porque las Odds ratio siempre se dan con su I C 95%. Veamos un ejemplo en el resumen de un artículo científico:

Es muy importante, una vez visto estos números y estos intervalos, dominarlos bien, saberlos situar bien. Veamos algunos ejemplos importantes para practicar en el manejo claro de números, orden e intervalos:

a.El número 0.75 es mayor que el número -0.85, pero la correlación -0.85 es mayor que la correlación 0.75.

b.El número 0.65 es mayor que el número -0.45 y la correlación 0.65 es también mayor que la correlación -0.45.

c.En el intervalo de correlaciones (-0.32, 0.45) el 0 está incluido.

d.En el intervalo de odds ratio (0.48, 1.55) el 1 está incluido.

e.En el intervalo de odds ratio (1.22, 1.67) el 1 no está incluido.

4.Ecuaciones.

Es interesante practicar con esta ecuación.

4.Concepto de probabilidad.

La noción de probabilidad es conceptualmente muy sencilla. Se trata del siguiente cociente:

Tan sencillo como esto. Entre todas las posibilidades que hay cuáles son las favorables. Si queremos saber la probabilidad del 1 en un dado es 1/6 porque aplicamos este cociente. Si queremos saber la probabilidad de cara en el lanzamiento de una moneda es 1/2 porque también aplicamos este cociente.

La noción de probabilidad condicionada es también muy importante conocerla porque muchas veces tenemos información ante la incertidumbre de un determinado suceso. Y no es lo mismo P(A) que P(A/B). No es lo mismo preguntarse por la probabilidad de A, sin más, que la probabilidad de A sabiendo que se ha producido el suceso B. Veamos esta noción:

Al saber que se ha producido el suceso B las cosas cambian, el campo de lo posible cambia. Si antes potencialmente todo era posible ahora sólo es posible que suceda algo dentro de B. Por eso, en general, cambia la probabilidad de A al saber que ha sucedido B.

Un ejemplo en nuestra base de datos. Con la información que tenemos podemos decir que la probabilidad de que una persona tenga bronquitis crónica es 6/22; o sea, 3/11; ó 0.2727 por uno; ó 27.27%.

Sin embargo, si sabemos que una persona es fumadora, entonces la probabilidad de que tenga bronquitis crónica pasa a ser de 5/13; o sea 0.3846 por uno; ó 38.46%.

6.Concepto de función de distribución.

Una función de distribución, dicho intuitivamente, no desde un punto de vista de matemática formal, es un dibujo de la variación de una variable.

Veamos las dos funciones de distribución o distribuciones más usuales:

a.La distribución Bernouilli:

b.La distribución normal (Campana de Gauss):

Lo hacemos con la variable Altura de nuestra base de datos.

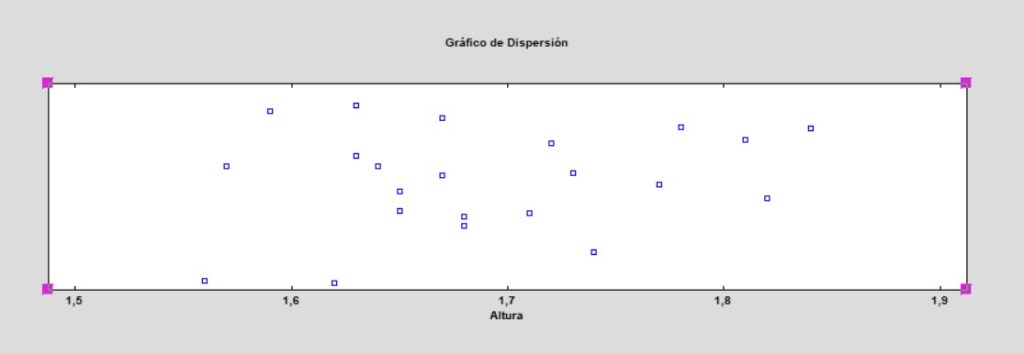
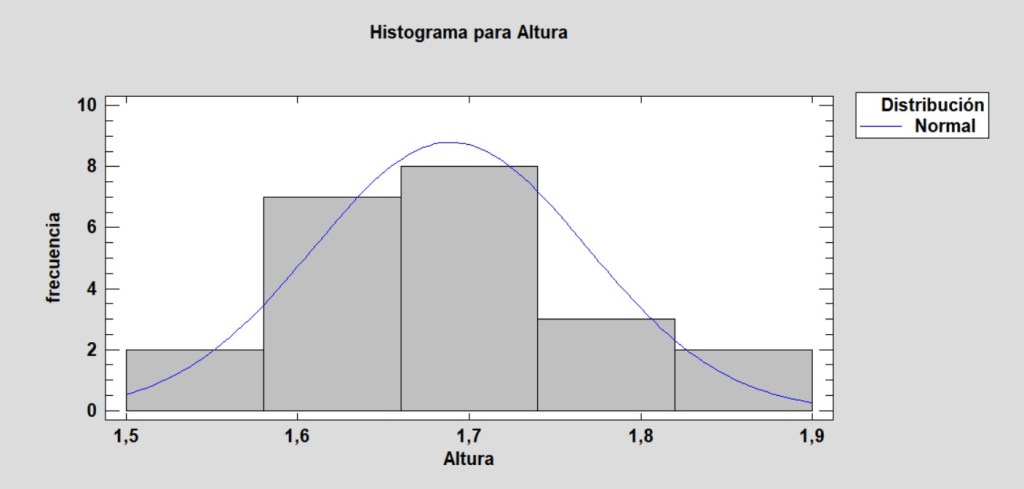
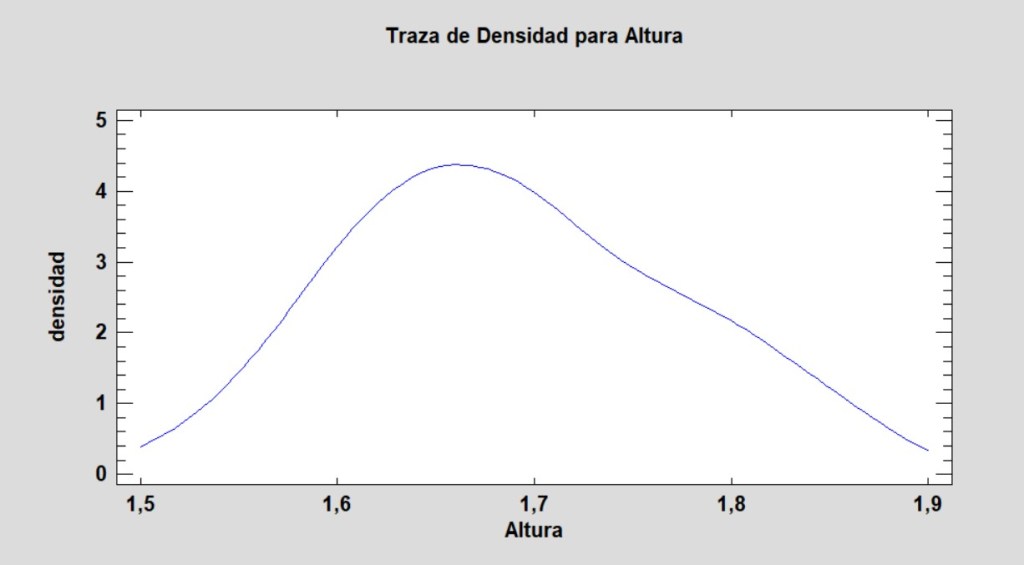
7.Poblaciones y muestras.

Cuando estudiamos entidades, en Ciencia, las integramos en Poblaciones. Pretendemos hablar de todas las entidades de esas poblaciones pero debemos contentarnos con estudiar una parte de esas entidades, las que tenemos en una muestra. A partir del estudio de esas muestras pretendemos decir cosas poblacionales.

Con la siguiente tabla veremos que tenemos ante nosotros una muestra de 214 mujeres con Anorexia, no los miles y miles de personas que tienen ese trastorno. Sin embargo, mediante esta muestra, calculando cosas a esa muestra podemos tratar de aproximarnos a lo que sería el conocimiento de toda la inmensa población de la que no tenemos información, ni tendremos, en realidad, nunca.